Referat.me
/ / Интеграл Пуассона

Название: Интеграл Пуассона

Вид работы: реферат

Рубрика: Математика

Размер файла: 108.53 Kb

Скачать файл: referat.me-217403.docx

Краткое описание работы: Определение интеграла Пуассона и ядра Пуассона, основные теоремы.

Интеграл Пуассона

Пусть ¦(x ) , g (x ) , x ÎR1 –суммируемые на [-p, p] , 2p- периодические, комплекснозначные функции. Через f * g(x) будем обозначать свертку

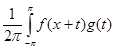f * g(x) =dt

Из теоремы Фубини легко следует, что свертка суммируемых функций также суммируема на [-p,p] и

cn ( f*g ) = cn ( f )× cn ( g ) , n = 0, ±1 , ±2 , ... ( 1 )

где { cn ( f )} -- коэффициенты Фурье функции f ( x ) :

cn = 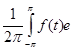-i n t dt , n = 0, ±1, ±2,¼

Пусть ¦ Î L1 (-p, p ) . Рассмотрим при 0 £ r < 1 функцию

¦r ( x ) = n ( f ) r| n | ei n x , x Î [ -p, p ] , ( 2 )

где ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦r (х) равны

cn ( fr ) = cn × r| n | , n = 0 , ±1, ±2, ¼ , а это согласно (1) значит, что ¦r ( x ) можно представить в виде свертки :

¦r ( x ) = 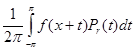, ( 3 )

где

, t Î [ -p, p ] . ( 4 )

Функция двух переменных Рr (t) , 0 £ r <1 , t Î [ -p, p ] , называется ядром Пуассона , а интеграл (3) -- интегралом Пуассона .

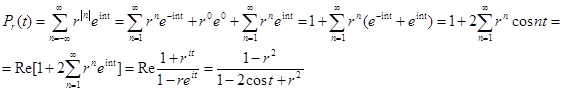
Следовательно,

Pr ( t ) = , 0 £ r < 1 , t Î [ -p, p] . ( 5 )

Если ¦Î L1 ( -p, p ) - действительная функция , то , учитывая , что

c-n ( f ) = `cn ( f ) , n = 0, ±1, ±2,¼, из соотношения (2) мы получим :

fr ( x ) =

= , ( 6 )

где

F ( z ) = c0 ( f ) + 2 ( z = reix ) ( 7 )

- аналитическая в единичном круге функция . Равенство (6) показывает, что для любой действительной функции ¦Î L1 ( -p, p ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция

u ( z ) = ¦r (eix ) , z = reix , 0 £ r <1 , x Î [ -p, p ] .

При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой

v (z) = Im F (z) = . ( 8 )

Утверждение1.

Пусть u (z) - гармоническая ( или аналитическая ) в круге | z | < 1+e ( e>0 ) функция и ¦ (x) = u (eix ) , xÎ[ -p, p ] . Тогда

u (z) = 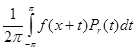( z = reix , | z | < 1 ) ( 10 ).

Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:

=, | z | < 1+ e .

Но тогда

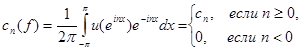
и равенство (10) сразу следует из (2) и (3).

Прежде чем перейти к изучению поведения функции ¦r (x ) при r®1 , отметим некоторые свойства ядра Пуассона:

а) ;

б) ;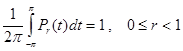

в) для любого d>0

Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦ (х) º 1.

Теорема 1.

Для произвольной (комплекснозначной) функции ( -p, p ) , 1 £ p < ¥ , имеет место равенство

;

если же ¦ (x) непрерывна на [ -p, p ] и ¦ (-p) = ¦ (p) , то

.

Доказательство.

В силу (3) и свойства б) ядра Пуассона

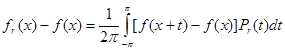( 12 )

Для любой функции , пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим

.

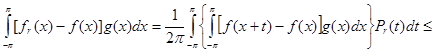
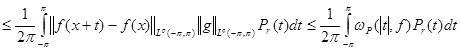Следовательно,

.

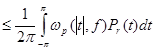Для данного e > 0 найдем d = d (e) такое, что . Тогда для r , достаточно близких к единице, мы получим оценку

.

Аналогично второе неравенство вытекает из неравенства

.

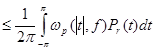Теорема 1 доказана.

Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.

Определение1.

Пусть функция суммируема на любом интервале (-А, А), А > 0 . Максимальной функцией для функции называется функция

где супремум берется по всем интервалам I , содержащим точку х.

Определение 2.

Оператор называется оператором слабого типа (р,р) , если для любого y > 0

.

Теорема 2 (Фату).

Пусть - комплекснозначная функция из . Тогда

для п.в. .

Доказательство.

Покажем, что для и

, ( 13 )

где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x) [1] . Для этой цели используем легко выводимую из (5) оценку

(К - абсолютная константа).

Пусть - такое число, что

.

Тогда для

.

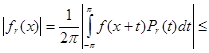
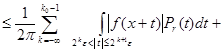
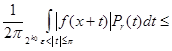
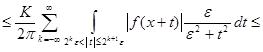
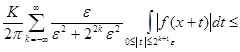
Неравенство (13) доказано. Используя затем слабый тип (1,1) оператора , найдем такую последовательность функций ,что

,

( 14 )

для п.в. .

Согласно (13) при xÎ (-2p,2p)

Учитывая , что по теореме 1 для каждого xÎ [-p, p] и (14)

Из последней оценки получим

при n®¥.

Теорема 2 доказана.

Замечание.

Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p, p] , когда точка reit стремится к eix по некасательному к окружности пути.

[1] Мы считаем , что f (x) продолжена с сохранением периодичности на отрезок [-2p,2p] (т.е.
f (x) = f (y) , если x,y Î [-2p,2p] и x-y=2 p ) и f (x) = 0 , если |x | > 2p .


Похожие работы