Название: Оценочный и сравнительный эксперимент

Вид работы: реферат

Рубрика: Математика

Размер файла: 122.08 Kb

Скачать файл: referat.me-216982.docx

Краткое описание работы: Обработка одноуровневого технологического эксперимента (выборка В Построить эмпирический закон распределения для данной выборки.

Оценочный и сравнительный эксперимент

1. Обработка одноуровневого технологического эксперимента (выборка В₁ ).

1.1 Построить эмпирический закон распределения для данной выборки.

342	321	324	325	365	347	287	317	313	318
330	330	277	310	331	313	298	325	296	327
337	318	329	345	324	344	277	359	355	299
283	289	328	356	319	307	327	337	346	290
332	322	366	282	344	314	321	310	304	301
317	316	339	363	323	329	349	382	294	320
308	313	300	335	311	359	318	296	320	319
280	317	314	376	321	292	291	333	300	319
302	322	346	323	315	323	329	333	328	304
265	325	320	349	353	301	302	277	292	300

при устанавливаем число :

величина интервала:

граница классов
277-292	284.5	10	-2	-20	4	40
292-307	299.5	14	-1	-14	1	14
307-322	314.5	26	0	0	0	0
322-337	329.5	21	1	21	1	21
337-352	344.5	9	2	18	4	36
352-367	359.5	8	3	24	9	72
367-382	374.5	2	4	8	16	32
	—	90	—	37	—	215

среднеквадратическое отклонение:

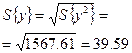
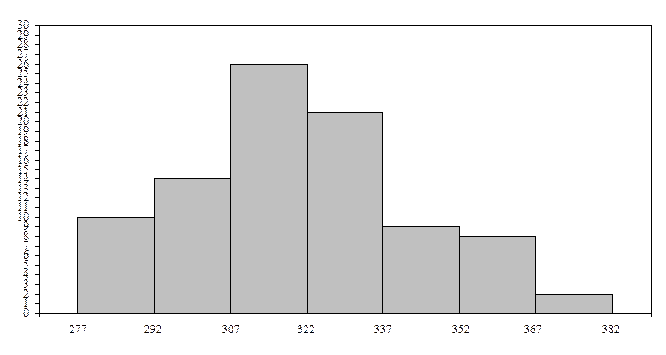
Эмпирический закон распределения выборки В₁

Гистограмма:

1.2 Определить точечные оценки (среднее, дисперсия).

Среднее значение:

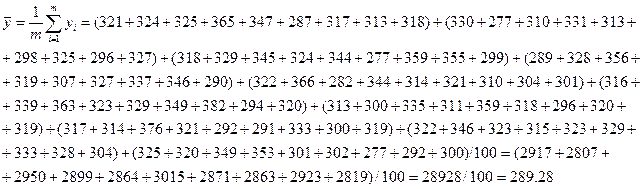
Дисперсия:

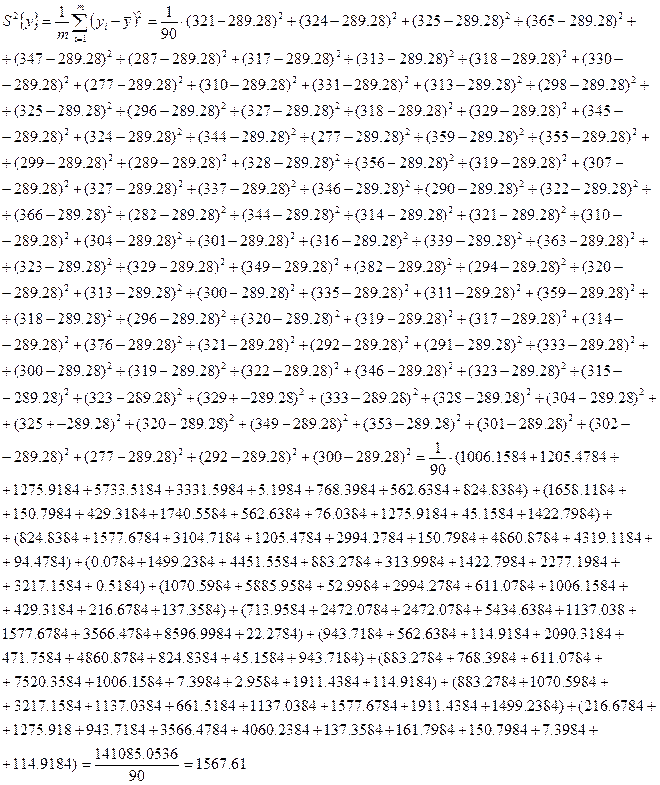
1.3 Определить относительные ошибки и доверительные интервалы для генерального среднего и генеральной дисперсии.

Абсолютная доверительная ошибка среднего:

при ,

Относительная доверительная ошибка среднего:

Границы доверительного интервала среднего значения:

Абсолютная доверительная ошибка дисперсии:

– относительная доверительная ошибка

дисперсии

Граница доверительного интервала дисперсии:

1.4 Спланировать объём выборки, если при определении среднего относительная ошибка не должна превышать 1%.

Для планирования объёма выборки из В₁ выбираем 3 значения: 314, 322, 321.

Выборка В^* .

Числовые характеристики В^* :

– среднее значение

Дисперсия:

Среднее квадратичное отклонение:

Квадратичная неровнота:

Абсолютная доверительная ошибка:

где ; ;

Относительная доверительная ошибка:

Доверительный объём измерений:

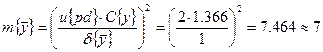
Реализуем выборку объёма . Для этого выбираем 2 значения: 324, 325, 319, 315, 311, 317, 313.

Выборка В^** .

Числовые характеристики В^** :

– среднее значение

Дисперсия:

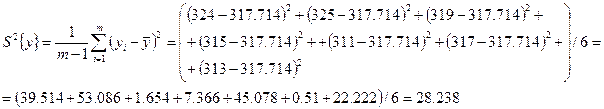
Среднее квадратичное отклонение:

Квадратичная неровнота:

Абсолютная доверительная ошибка:

где ; ;

Относительная доверительная ошибка:

1.5 Проверить гипотезу о пропорциональности технологического параметра для заданной выборки.

Проверка гипотезы осуществляется по критерию х² :

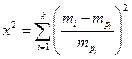
где – объём выборки; – частота попадания в i – классе; k – число классов; – вероятность попадания в i – интервал.

где ; – число степени свободы

Рассмотрим гипотезу , при конкурирующей

Введём новое значение , где ;

i	интервал
1	277-292	284.5	0.31	0.07	0.1217	0.0279	0.0938	8.442	1.558	0.184
2	292-307	299.5	0.07	0.45	0.0279	0.1736	0.1457	13.113	0.887	0.068
3	307-322	314.5	0.45	0.83	0.1736	0.2967	0.1231	11.079	14.921	1.347
4	322-337	329.5	0.83	1.205	0.2967	0.3944	0.0977	8.793	12.207	1.388
5	337-352	344.5	1.205	1.58	0.3944	0.4429	0.0485	4.365	4.635	1.062
6	352-367	359.5	1.58	1.96	0.4429	0.4750	0.0321	2.889	5.111	1.769
7	367-382	374.5	1.96	2.34	0.4750	0.4903	0.0153	1.377	0.623	0.452
6.27

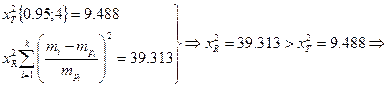гипотеза о нормальности технологического процесса не принимается.

1.6 Проверить наличие резко выделяющихся значений в выборке (метод ).

и находятся в пределах интервала (; ), следовательно резко выделяющихся значений в выборке нет.

2. Обработка сравнительного технологического эксперимента.

Подготовка данных: сформировать из исходного массива В₁ методом рандомизации две выборки малого объёма В₂ и В₃ для дальнейших исследований.

2.1 Определить числовые характеристики выборок В₂ и В₃ .

	В2	В3
1	347	287
2	313	298
3	344	277
4	307	327
5	314	321
6	329	349
7	359	318
8	292	291
9	323	329
10	301	302

Числовые характеристики выборки В₂ .

Среднее значение:

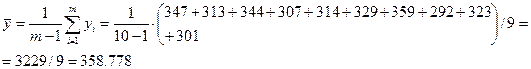Дисперсия:

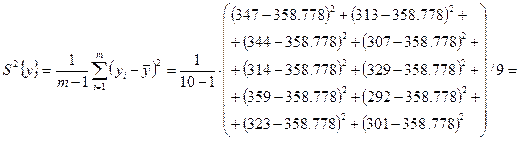
Среднее квадратичное отклонение:

Коэффициент вариации:

Квадратичная неровнота:

Абсолютная доверительная ошибка среднего значения:

где ; ;

Относительная доверительная ошибка среднего значения:

Числовые характеристики выборки В₃ .

Среднее значение:

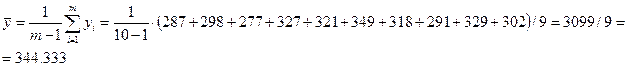
Дисперсия:

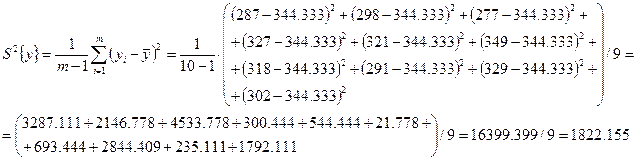
Среднее квадратичное отклонение:

Коэффициент вариации:

Квадратичная неровнота:

Абсолютная доверительная ошибка среднего значения:

где ; ;

Относительная доверительная ошибка среднего значения:

2.2 Определить доверительные интервалы для генерального среднего и генеральной дисперсии.

Доверительный интервал для среднего значения выборки В₂ :

Доверительный интервал для дисперсии:

;

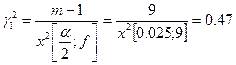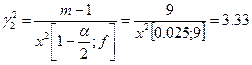
где ;

Доверительный интервал для среднего значения выборки В₃ :

Доверительный интервал для дисперсии:

;

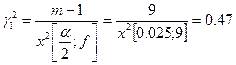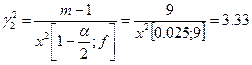
где ;

2.3 Проверка гипотезы о равенстве генеральных средних выборок В₂ и В₃ : ; .

Сравниваем две дисперсии нормальных генеральных совокупностей с числом степеней свободы:

;

;

Оцениваем возможность принятия гипотезы .

При альтернативной гипотезе и доверительной вероятности находим:

т.к. , то выдвинутую гипотезу об однородности дисперсии или равной точности двух рядов измерений и надо принять.

Сравниваем две средние из нормальных распределений генеральных совокупностей.

Если доказана, то используется критерий :

,

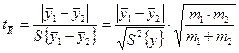где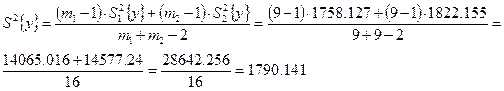

; ;

; ;

Проверим гипотезу о равенстве средних:

при конкурирующей гипотезе

Затем находим расчётное значение критерия Стьюдента:

и его табельное значение

Т.к. , то генеральные средние и статически не различаются. Гипотеза принимается.