Название: Практика перевода числа из одной системы счисления в другую + блок-схема алгоритма определения наименьшего числа
Вид работы: реферат
Рубрика: Математика
Размер файла: 22.17 Kb
Скачать файл: referat.me-216996.docx
Краткое описание работы: Задание №1, вопрос №1: Перевести заданные числа в десятичную систему счисления. ТАБЛИЦА С и с т е м а с ч и с л е н и я 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 0 0 0 0
Практика перевода числа из одной системы счисления в другую + блок-схема алгоритма определения наименьшего числа
Задание №1, вопрос №1: Перевести заданные числа в десятичную систему счисления.
ТАБЛИЦА
С и с т е м а с ч и с л е н и я |
|||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 1 0 | 2 | 2 |
| 3 | 1 1 | 3 | 3 |
| 4 | 1 0 0 | 4 | 4 |
| 5 | 1 0 1 | 5 | 5 |
| 6 | 1 1 0 | 6 | 6 |
| 7 | 1 1 1 | 7 | 7 |
| 8 | 1 0 0 0 | 1 0 | 8 |
| 9 | 1 0 0 1 | 1 1 | 9 |
| 10 | 1 0 1 0 | 1 2 | A |
| 11 | 1 0 1 1 | 1 3 | B |
| 12 | 1 1 0 0 | 1 4 | C |
| 13 | 1 1 0 1 | 1 5 | D |
| 14 | 1 1 1 0 | 1 6 | E |
| 15 | 1 1 1 1 | 1 7 | F |
| 16 | 1 0 0 0 0 | 2 0 | 1 0 |
А) 1101101,1102
Для перевода целого числа из двоичной системы в десятичную необходимо цифры умножать на двойку в степени номера позиции (номер позиции начинается с нуля и нумеруется с права на лево). В не целых числах та часть числа, которая стоит после запятой, переводится отдельно, и дописывается к уже полученному числу.
11011012= 1x20 +0x21 +1x22 +1x23 +0x24 +1x25 +1x26 =10910
Переведём дробную часть:
1102= 0x20 +1x21 +1x22 = 610
Итак, мы получаем, что 1101101,1102=109,610
Б) 226,518
Для того, чтобы перевести число из восьмиричной системы в десятичную, необходимо сначала перевести его по таблице в начале контрольной в двоичную, а затем выше описанным методом в десятичную систему. Перевод по таблице делается справа налево, по одной цифре, причём в двоичном варианте должны выходить триады (цифры по три штуки), и если символов меньше, необходимо при переводе каждой цифры дописывать слева нули.
Мы получаем, что 226,518=10010110,1010012
По правилу перевода числа из двоичной системы в десятичную получаем, что 10010110,1010012=150,4110
Итого: 226,518=150,4110
В) ВС16
Используем метод, описанный в числе «Б», с той разницей, что в двоичном коде мы должны получить тетрады (цифры по четыре штуки).
Получаем, что ВС16=101111002
Затем, способом перевода двоичного числа в десятичное выясняем, что:
ВС16=18810
Задание №1, вопрос №2: Выполнить указанные действия в заданной системе счисления.
А)
10011 2
+ 110 2
= 11001 2
Б)
632 8
- 24 8
= 626 8
В)
643 16
+ 6 D 16
= 6 B 0 16
Задание №1, вопрос №3: Заданные чиста и полученные результаты арифметических операции пункта 2 перевести в десятичною систему счисления и выполнить проверку полученных результатов в десятичной системе счисления.
А) Способом, описанным в задании №1, вопросе №1, подвопросе А, получаем, что:
10011 2 =19 10
110 2 =6 10
11001 2 =25 10
Б) Способом, описанным в задании №1, вопросе №1, подвопросе Б, получаем, что:
632 8 =410 10
24 8 =20 10
626 8 =406 10
В) Способом, описанным в задании №1, вопросе №1, подвопросе В, получаем, что:
643 16 =1603 10
6 D 16 =109 10
6 B 0 16 =1712 10
ВЫВОД: Так как все операции с числами сходятся в десятичной системе счисления, и при переводе чисел заданий с ответами тоже, то предыдущее задание выполнено верно.
Задание №1, вопрос №4: Перевести заданные в десятичной системе счисления числа в системы с основаниями 2, 8 и 16:
65210
984,65210
23674,56677510
Ответ:
Для того, чтобы перевести число из десятичной системы в любую другую, необходимо это число делить на число – основание той системы, в которую переводится число. Соответственно, эти числа – 2, 8, 10 и 16. Остатки необходимо фиксировать и нумеровать. Число, полученное в результате деления – делим ещё раз, и так до тех пор, пока вновь полученное число уже само не станет остатком, т. е. будет меньше основания – оно замыкает цепочку остатков. Затем остатки, начиная с последнего, переписываем в число, которое является переведённым в другую систему счисления.
Разделим число 63210 на 2, переведя его таким образом в двоичную систему счисления:
632/2=316, остаток№1 (A1)=0;
316/2=158, A2=0
158/2=79, A3=0
79/2=39, A4=1
39/2=19, A5=1
19/2=9, A6=1
9/2=4, A7=1
4/2=2, A7=0
2/2=1, A8=0
A9=1.
Теперь напишем остатки с последнего, и получим число 63210 в двоичной системе, оно = A9+A8+A7+A6+A5+A4+A3+A2+A1 =
= 10011110002
Путём такого деления узнаём, что:
63210 = 10011110002 = 27816 = 11708
984,65210=1111011000,10011110002=3D8, 27816=1730,11708
23674,56677510=57CA,8A5F716=56172,21227678 =
= 101110001111010,100010100101111101112
Задание №1, вопрос №5: Перевести заданные в одной системе счисления числа в другую указанную в скобках систему счисления.
А) 333,13 8 (8 - 2)
Б) 11101010,111112 (2-8)
В) 2336,748 (8-16)
Для того, чтобы перевести число «В» необходимо сначала перевести его в двоичную систему счисления. Используя метод, изложенный при решении задания №1, вопроса№1, подвопроса «Б» и «В» получаем:
333,138=11011011,10112
11101010,111112=352,378
2336,748=4DE,3C16
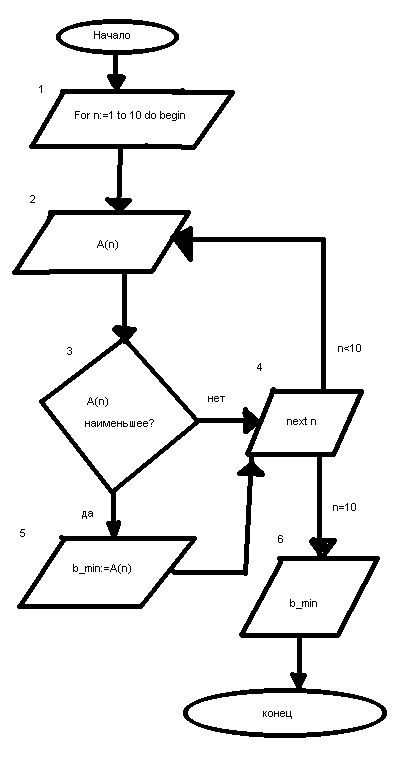
Задание №2: Блок схема алгоритма определения минимального из десяти заданных чисел.
Похожие работы
-
Системы счисления 2
СИСТЕМЫ СЧИСЛЕНИЯ Система счисления - это способ записи чисел. 64, / Системы счисления Позиционные- Позиционные системы счисления - системы записи чисел, в которых значение каждой цифры числа зависит от ее положения (позиции) в последовательности цифр.
-
по Высшей математике 2
1*11⁴+1*11³+6*11²+3*11¹+2*11⁰+9*11⁻¹+9*11⁻²+3*11⁻³=14641+1331+726+33+2+0,818+0,074+0,002=
-
Перевод мер угла в градусной часовой системе
Перевод мер угла в градусной системе Классическая запись меры угла в градусной системе выглядит следующим образом: Эта запись обозначает, что мера угла содержит А градусов, В минут и С секунд.
-
Китайская система счисления
1. Структура системы счисления Китая. Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять. (Смотреть таблицу обозначений чисел.)
-
Системы счисления и основы двоичных кодировок
История развития систем счисления. Непозиционная, позиционная и десятичная система счисления. Использование систем счисления в компьютерной технике и информационных технологиях. Двоичное кодирование информации в компьютере. Построение двоичных кодов.
-
Системы счисления 4
Цель работы Понять принципы позиционной системы счисления. Научиться переводить числа из одной системы счисления в другую. Уметь производить арифметические действия над числами, представленными в различных системах счисления.
-
Системы счисления
Система счисления – это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, которые существовали ранее и существуют теперь, можно разделить на позиционные и непозиционные. Знаки, которые используются при записи чисел, называются цифрами.
-
Египетские дроби
Египетские дроби Одним из древнейших письменных документов человечества является папирус Райнда, датируемый ориентировочно 1600 г. до н.э. Замечательно, что это также древнейшее математическое сочинение. Древние египтяне записывали рациональные дроби как суммы чисел, обратных натуральным: 2/5 = 1/3 + 1/15, 6 / 7 = 1/2 + 1/3 + 1/42 и т. д.
-
Модели и методы принятия решений
Нахождение экстремумов функций методом множителей Лагранжа. Выражение расширенной целевой функции. Схема алгоритма численного решения задачи методом штрафных функций в сочетании с методом безусловной минимизации. Построение линий ограничений.
-
Обобщённая задача о фальшивых монетах
Классическую задачу об одном мешке с фальшивыми монетами можно найти во многих популярных книжках по математике. Говорят, что во время второй мировой войны англичане «сбросили» эту задачу над немецкими солдатами с целью их дезорганизации.