Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых)

Лабораторная работа № 4.

Приближенный метод решения интегралов.

Метод прямоугольников (правых, средних, левых).

Гребенникова Марина

12-А класс

Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида где f(x) -данная функция, непрерывная на отрезке [a; b]. Если функция f(x) задана формулой и мы умеем найти неопределенный интеграл F(x), то определенный интеграл вычисляется по формуле Ньютона-Лейбница:
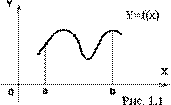
Если же неопределенный интеграл данной функции мы найти не умеем, или по какой-либо причине не хотим воспользоваться формулой Ньютона-Лейбница или если функция f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла можно использовать метод прямоугольников (правых, левых, средних). При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если f(x)>=0 на отрезке [a; b], то численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1) Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.

Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка .

Точки деления будут: x₀ =a; x₁ =a+h; x₂ =a+2*h, ... , x_n-1 =a+(n-1)*h; x_n =b.

Числа y₀ , y₁ , y₂ , ... , y_n являются ординатами точек графика функции, соответствующих абсциссам x₀ , x₁ , x₂ , ... , x_n (рис. 1.2).

Строим прямоугольники. Это можно делать несколькими способами:

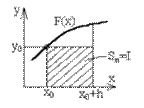Левые прямоуголики (слева на право)

Правые прямоугоники (построение справа на лево)

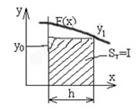
Средние прямоугольники (посредине)

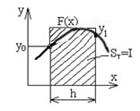
Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.

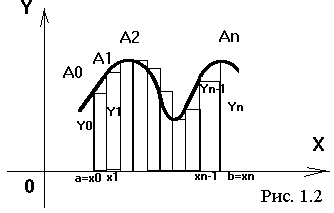
h=(b-a)/n –ширина прямоугольников

Формула левых прямоугольников:

(1.3)

Формула правых прямоугольников:

(1.4)

Формула средних прямоугольников.

S_средих = (S_правых + S_левых ) /2

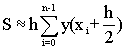(1.5)

Программа вычисления по методу левых прямоугольников.

Programlevii;{Метод левых прямоугольников}
usescrt;
vari,n:integer; a,b,h,x,xb,s:real;
functionf(x:real):real;
beginf:=(1/x)*sin(3.14*x/2); end;
begin
clrscr;
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите количество отрезков '); readln(n);
h:=(b-a)/n; s:=0; xb:=a;
fori:=0 ton-1 do
beginx:=xb+i*h; s:=s+f(x)*h; end;
writeln('Интеграл равен ',s:12:10); readln;
end.

a=1 b=2 n=10 S= 18,077

a=1 b=2 n=20 S= 18, 208

a=1 b=2 n=100 S= 18, 270

Программа вычисления по методу правых прямоугольников .

a=1 b=2 n=10 S=18,05455

a=1 b=2 n=20 S=18,55555

a=1 b=2 n=100 S= 18,2734

Программа вычисления по методу средних прямоугольников.

a=1 b=2 n=10 S=18,07667

a=1 b=2 n=20 S=18,368

a=1 b=2 n=100 S= 18,156

Заключение и выводы.

Таким образом очевидно, что при вычислении определенных интегралов методами прямоугольников не дает нам точного значения, а только приближенное.

Чем больше значение n, тем точнее значение интеграла..