Referat.me
/ / Теория случайных процессов

Название: Теория случайных процессов

Вид работы: реферат

Рубрика: Математика

Размер файла: 106.19 Kb

Скачать файл: referat.me-217423.docx

Краткое описание работы: Вычисление спектральной плотности сигнала по выборке его синусоидальных составляющих.

Теория случайных процессов

Министерство образования России

Специальные главы математики

Пояснительная записка

по теме: “ Теория вероятностей

и случайных процессов”

Студент: Ёлгин Д.Ю.

Куратор: Хоменко В.М.

НГТУ - 97

1. Случайныи образом выберем семейство кривых:

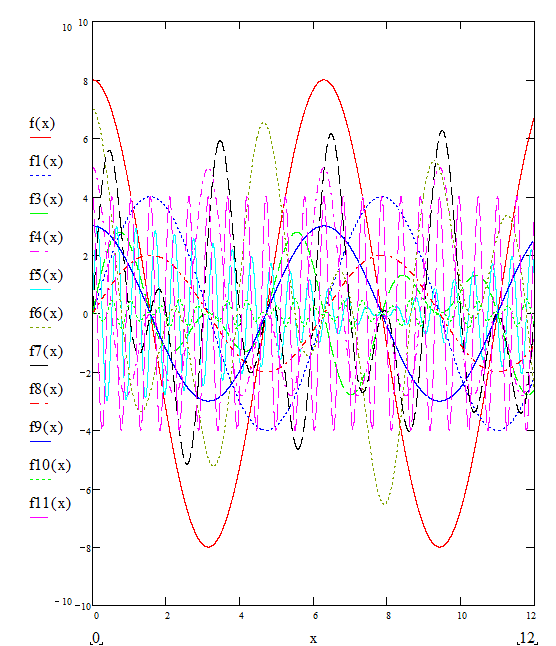
Примечание:

Наугад выбираются 14 кривых. Все кривые имеют синусоидальную форму. Область значений не привышает интервал [ -12; 12 ]. Для каждой функции вычисляем значения в точках 0, 2, 4, 6, 8, 10, 12 и составляем матрицу М1.

1. Составим матрицу рабочих значений М1:

0

2

4

6

8

10

12

x1

8

-3,329

-5,229

7,681

-1,164

-6,713

6,751

x2

0

3,637

-3,027

-1,118

3,957

-2,176

-2,146

x3

0

-1,227

-1,235

1,594

0,565

0,777

-2,609

x4

5

-1,998

-2,758

3,17

-0,309

-0,647

-0,54

x5

0

-2,502

-1,606

0,276

-0,086

-0,725

1,086

x6

7

-0,324

1,008

-1,245

-6,437

0,99

-2,705

x7

0

0

0

0

0

0

0

x8

0

1,819

-1,514

-0,559

1,979

-1,088

-1,073

x9

3

-1,248

-1,961

2,881

-0,437

-2,517

2,532

x10

0

-0,161

-0,317

0,26

0,026

0,372

-0,394

x11

4

1,697

-2,561

-3,869

-0,722

3,257

3,485

x12

0

-2,377

0,44

-0,943

-3,79

-0,888

-0,91

x13

2

-0,832

-1,307

1,92

-0,291

-1,678

1,688

x14

0

0,909

-0,757

-0,279

0,989

-0,544

-0,537

4. Вычислим m[t] :

t

0

2

4

6

8

10

12

m[t]

2,071429

-0,424

-1,48743

0,697786

-0,40857

-0,82714

0,330571

1. Составим корреляционную матрицу М2:

Корелляционная матрица

0

2

4

6

8

10

12

0

162,7092

-36,6317

-64,2259

64,14459

-59,8507

-46,1746

56,60024

2

50,93338

11,23673

-48,7464

33,38392

25,55703

-26,5632

4

62,29164

-45,8419

-15,0293

43,78402

-42,4137

6

102,2796

-1,99387

-72,1782

50,37741

8

78,75916

-6,8851

-3,53313

10

73,80887

-41,2532

12

89,49557

1. Составим таблицу дисперсий и сигм:

0

2

4

6

8

10

12

Дисперс

162,7092

50,93338

62,29164

102,2796

78,75916

73,80887

89,49557

Сигма

12,75575

7,136762

7,892505

10,11334

8,874636

8,591209

9,46021

1. Сделаем нормировку М2 на наборе соответствующих сигм:

Нормированная кор-матрица

0

2

4

6

8

10

12

0

1

-0,40239

-0,63795

0,497232

-0,5287

-0,42135

0,469042

2

1

0,199491

-0,67538

0,527091

0,416826

-0,39344

4

1

-0,57432

-0,21457

0,645723

-0,56805

6

1

-0,02222

-0,83073

0,526551

8

1

-0,0903

-0,04208

10

1

-0,50758

12

1

1. Вычислим значения нормированной функции p[t] :

t

0

2

4

6

8

10

12

p[t]

1

-0,23289

-0,48014

0,549149

-0,22664

-0,4074

0,469042

1. По найденным точкам используя функцию ошибки вычислим

коэффициенты a1 и a1 графика y = a0 + a1x и выберем её в силу оптимальности:

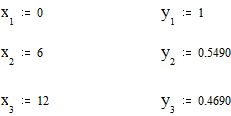
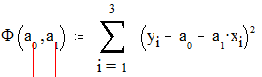
Составим систему уравнений:

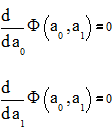
Из них вычислим a0 и a1 и запишем уравнение оптимальной прямой:

9. Построим график функции p[t] :

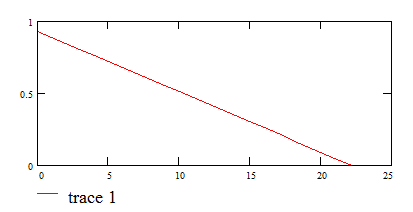
10. Вычислим нормированную спектральную плотность S(w) :

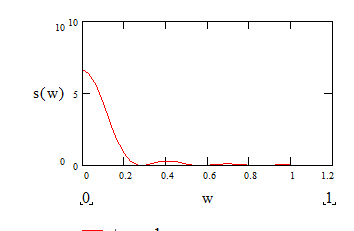
1. Построим график S(w) :

Похожие работы