Название: Собственные вектора и собственные значения линейного оператора

Вид работы: реферат

Рубрика: Математика

Размер файла: 122.48 Kb

Скачать файл: referat.me-217652.docx

Краткое описание работы: Понятие собственных векторов и собственных значений, их свойства и характеристики, порядок нахождения собственных векторов оператора. Критерии определения независимости и ортогональности собственных векторов. Факторы и теоремы положительных матриц.

Собственные вектора и собственные значения линейного оператора

РЕФЕРАТ

"Собственные вектора и собственные значения линейного оператора"

Понятие собственные векторы и собственные значения

Перед тем как определить понятие собственные вектора, покажем его на наглядном примере. На рисунке 1, красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространство.

Рис. 1

Определение. Ненулевой вектор x называется собственным вектором линейного оператора , если найдется такое число λ, называемое собственным значением линейного оператора, что

(x) = λ· x (1)

Равенство (1) означает, что вектор x, подвергнутый действию линейного оператора, умножается на число λ. Появляется коллинеарный вектор. Среди векторов линейного векторного пространства могут существовать такие, воздействие оператора на которые переводит эти векторы в коллинеарные самим себе. Если на таких векторах построить базис, преобразования линейной алгебры значительно упростятся.

Не всякий линейный оператор обладает собственными векторами. Например, в геометрической плоскости R² оператор поворота на угол, не кратный π, не имеет ни одного собственного вектора, поскольку ни один ненулевой вектор после поворота не останется коллинеарным самому себе.

Решим задачу нахождения собственных векторов оператора. Запишем равенство (1) в матричной форме:

P · X = λ· X

Преобразуем матричное уравнение:

P·X – λ ·X = 0 или (P – λ ·E) X =0

Матричное уравнение всегда имеет нулевое решение:

X=0=

Для существования ненулевых решений ранг матрицы коэффициентов должен быть меньше числа переменных r<n, т.е. число линейно независимых уравнений должно быть меньше числа переменных. В этом случае должно быть выполнено условие

|P – λ· E |=0 (2)

Расписав уравнение (2) относительно λ подробнее, получим

|P – λ· E | =

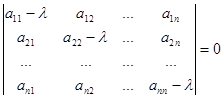
Раскрыв определитель, получим уравнение n-й степени относительно λ:

Которое называется характеристическим уравнением оператора . Корни уравнения называются характеристическими или собственными числами оператора. Множество всех собственных чисел оператора называется спектром этого оператора. Многочлен левой части уравнения называется характеристическим многочленом.

Решив характеристическое уравнение, получаем собственные числа λ₁ , λ₂ , …, λ_n . Для каждого найденного собственного значения λ_i найдем ненулевые векторы ядра оператора P – λ_i E . Именно они будут собственными векторами, соответствующими собственному значению λ_i . Другими словами, необходимо решить однородную систему уравнений (P – λ_i E ) X =0. Ее общее решение дает всю совокупность собственных векторов, отвечающих λ _i .

Общее решение однородной системы, как известно, структурировано. Оно представляет собой линейную комбинацию фундаментального набора линейно независимых решений (векторов). Число линейно независимых векторов в фундаментальном наборе называется геометрической кратностью собственного значения λ _i . Вводиться также алгебраическая кратность – кратность λ _i как корня характеристического многочлена.

Независимость собственных векторов

Существование линейно независимых векторов среди собственных, отвечающих различным собственным числам λ₁ , λ₂ , …, λ _n , определяется следующей теоремой.

Собственные векторы x₁ , x ₂ , …, x_n оператора, отвечающие различным собственным значениям λ₁ , λ₂ , …, λ _n , линейно независимы.

На n линейно независимых собственных векторах можно построить базис n-мерного линейного векторного пространства.

Замечание. Определитель матрицы P – λ E (соответственно характеристический многочлен) не зависит от выбора базиса.

|P’ – λ E | =|T^-1 PT – λ E | =|T^-1 PT- λ T^-1 E T| =|T^-1 P- λ E T| =|T^-1 ||P- λ E T| |T|=|P- λ E T|

Следовательно, при переходе к новому базису собственные числа сохраняются.

Пример. Найти собственные значения и собственные векторы линейного оператора , заданного матрицей P= в пространстве R² .

Решение. Составим характеристическое уравнение:

|P – λ· E | == λ² -5 λ+4=0

Из квадратного уравнения найдем собственные значения линейного оператора λ₁ =1, λ₂ =4. Чтобы найти собственные векторы, решим матричные уравнения:

(P – λ₁ E ) X =0 и (P – λ₂ E ) X =0

В развернутом виде

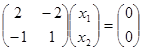и

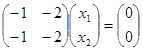
Соответствующие однородные системы:

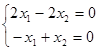
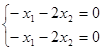
Общие решения систем:

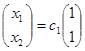и 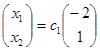, где с₁ , с₂ є R

Таким образом, множество собственных векторов, отвечающих собственным значениям λ₁ =1, λ₂ =4, имеет вид ; , где с₁ , с₂ є R. Векторы a₁ =(1, 1), a₂ =(-2, 1), например, являются линейно независимыми. Они могут быть приняты в качестве нового базиса в пространстве R² .

Пусть e₁ , e₂ , …, e_n – собственные векторы линейного оператора в пространстве Rⁿ , которые примем в качестве базиса. Тогда разложение векторов (e₁ ), (e₂ ), …, (e_n ) по базису e₁ , e₂ , …, e_n примет вид

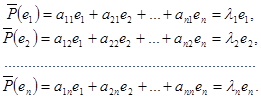
Отсюда следует, что a_ij = λ _i , если i=j и a_ij =0, если i≠j. Поэтому в базисе, составленном из собственных векторов, матрица оператора будет иметь диагональный вид:

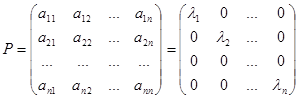
Симметричный оператор

Определение. Линейный оператор в евклидовом пространстве Rⁿ называется симметричным, если для любых векторов x и y из пространства Rⁿ выполняется равенство

((x), y)= (x, (y))

Для того чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была симметрична.

Рассмотрим для простоты евклидово пространство R² . Пусть в ортобазисе e₁ , e₂ заданы векторы x=(x₁ , x₂ ), y=(y₁ , y₂ ). Линейные операторы ₁ и ₂ определены своими матрицам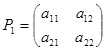и:

и .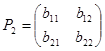

Вычислим векторы ₁ (x) и ₂ (y):

,

.

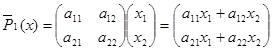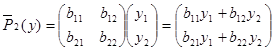Найдем скалярные произведения ((x), y) и (x, (y)):

( (x), y)=(a₁₁ x₁ +a₁₂ x₂ ) y₁ +(a₂₁ x₁ +a₂₂ x₂ ) y₂ =a₁₁ y₁ x₁ +a₁₂ y₁ x₂ +a₂₁ y₂ x₁ +a₂₂ y₂ x₂ ,

(x, (y))= (b₁₁ y₁ +b₁₂ y₂ ) x₁ +(b₂₁ y₁ +b₂₂ y₂ ) x₂ =b₁₁ x₁ y₁ +b₁₂ x₁ y₂ +b₂₁ x₂ y₁ +b₂₂ x₂ y₂ .

Найдем разность скалярных произведений:

(( x ), y ) – ( x , ( y )) = ( a ₁₁ - b ₁₁ ) x ₁ y ₁ +( a ₂₁ - b ₁₂ ) x ₁ y ₂ +( a ₁₂ - b ₂₁ ) x ₂ y ₁ +( a ₂₂ - b ₂₂ ) x ₂ y ₂ .

Если для любых векторов x и y из пространства R² равенство

(( x ), y ) – ( x , ( y ))=0 (3)

Выполнено (необходимость), то верна система

a₁₁ =b₁₁ ,

a₂₁ =b₁₂ ,

a₁₂ =b₂₁ , (4)

a₂₂ =b₂₂ ,

и обратно: если условия (4) соблюдены для любых векторов x и y, то равенство (3) выполнено (достаточность). Система равенств (4) означает, что ₁ =₂ =.

Ортогональность собственных векторов

Собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимо ортогональны.

Пусть x и y – собственные векторы оператора , соответствующие собственным числам λ₁ и λ₂ , причем λ₁ ≠ λ₂ . По определению симметричного оператора:

((x), y)= (x, (y))

Подставив сюда правые части равенства ((x))= λ₁ x , ((y))= λ₁ y , получим

(λ₁ x , y)=( x , λ₂ y ) . Вынесем числа λ₁ и λ₂ , за знак скалярного произведения, перенесем слагаемые влево и разложим на множители: (λ₁ – λ₂ ) (x, y)=0

Поскольку λ₁ ≠ λ₂ , получаем (x, y)=0, что и означает взаимную ортогональность векторов x и y.

Отметим другие важные свойства симметричного оператора.

1) Характеристическое уравнение симметричного оператора имеет только действительные корни.

2) Если в евклидовом пространстве Rⁿ задан симметричный оператор , то в Rⁿ существует ортонормированный базис e₁ , e₂ , …, e_n , составленный из собственных векторов .

3) Если все собственные числа λ₁ , λ₂ , …, λ _n симметричного оператора положительны, то ((x), x) > 0 для любого ненулевого вектора x.

Положительные матрицы

Квадратная вещественная матрица A = (a_ij ) называется положительной, если все её элементы положительны: a_ij > 0.

Теорема Перрона (частный случай теоремы Перрона-Фробениуса): Положительная квадратная матрица A имеет положительное собственное значение r, которое имеет алгебраическую кратность 1 и строго превосходит абсолютную величину любого другого собственного значения этой матрицы. Собственному значению r соответствует собственный вектор e_r , все координаты которого строго положительны. Вектор e_r – единственный собственный вектор A (с точностью до умножения на число), имеющий неотрицательные координаты.

Список литературы

1. Арутюнов Ю.C. и др. Высшая.математика: Методические указания и контрольные задания (с программой) для студентов-заочников инженерно-технических специальностей вузов. 3-е изд. М.: Высш. шк., 2005. 144 с.

2. Высшая математика: Программа, методические указания и контрольные задания для студентов-заочников иижеиерио-техиических специальностей сельскохозяйственных вузов. 4-е изд., перераб. М.: Высш.шк., 2005. 110 с.

3. Мироненко Е.С. Высшая математика: методические указания и контрольные задания для студентов-заочников инженерных специальностей вузов. М.: Высш. шк., 2008. 110 с.

4. Зимина О.В. и др. Высшая математика. 2-е изд., испр. М.: Физматлит, 2009. 368 с. (Решебиик).