Referat.me / Математика / Решение нелинейных уравнений

Название: Решение нелинейных уравнений

Вид работы: контрольная работа

Размер файла: 115.13 Kb

Скачать файл: referat.me-218337.docx

Краткое описание работы: Задание №1 Отделить корни уравнения графически и уточнить один из них: · методом половинного деления; · методом хорд; · методом касательных; · методом секущих;

Решение нелинейных уравнений

Задание №1

Отделить корни уравнения

графически и уточнить один из них:

· методом половинного деления;

· методом хорд;

· методом касательных;

· методом секущих;

· методом простой итерации;

с точностью ε=0,001.

Создать функции, реализующие указанные методы, построить графическую иллюстрацию методов, результаты проверить с помощью встроенных функций, оценить точность полученных значений.

1. Метод бисекции (деления отрезка пополам)

Метод бисекции или метод деления отрезка пополам — простейший численный метод для решения нелинейных уравнений вида F(x)=0. Предполагается только непрерывность функции F(x).

Графическое представление метода бисекций

Решим задание в пакете Маткад:

2. Метод хорд (метод линейной интерполяции)

Идея метода состоит в том, что по двум точкам и построить прямую (то есть хорду, соединяющую две точки графика) и взять в качестве следующего приближения абсциссу точки пересечения этой прямой с осью Ox .

Графическое представление метода хорд

Решим задание в пакете Маткад:

3. Метод касательных (Ньютона)

Графическое представление метода касательных

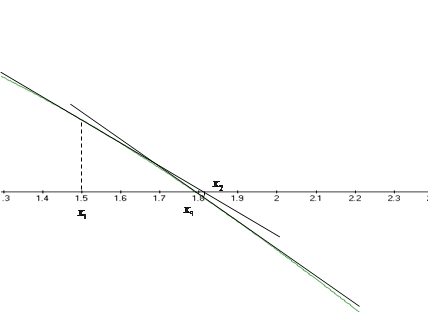
Решим задание в пакете Маткад:

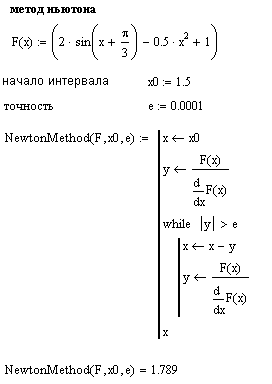
4. Метод секущих

Графическое представление метода секущих

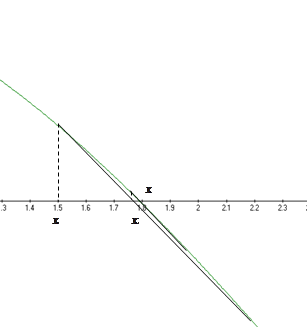
Решим задание в пакете Маткад:

5. Метод простой итерации

Введем функцию:

Графическое представление метода простой итерации

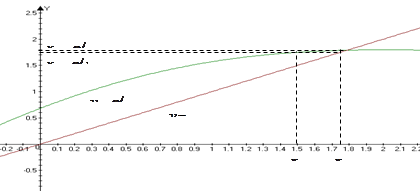
Решим задание в пакете Маткад:

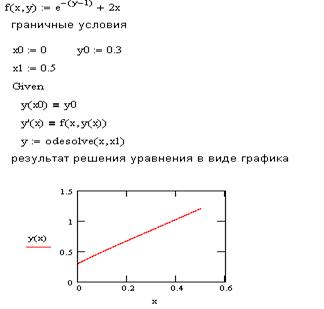
Задание №2

Решить задачу Коши для дифференциального уравнения на отрезке [a,b] при начальном заданном условии и шаге интегрирования h:

1. методом Эйлера;

2. методом Рунге – Кутта 4 – го порядка точности.

3. проверить решение с помощью встроенных функций пакета MathCAD.

В решении оставлять 5 цифр после запятой.

№ вари-анта	Функция	Интервал	y0	Шаг
23		[0;0,5]	y(0)=0,3	0,05

1. Метод Эйлера

Решим задание в пакете Маткад:

2. Метод Рунге – Кутта 4 – го порядка точности

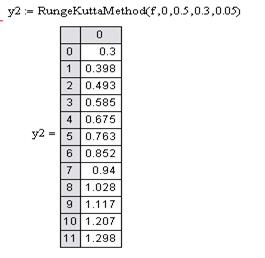
Проверим решение с помощью встроенных функций пакета MathCAD

Похожие работы

Решение нелинейных уравнений с одной переменной
Раздел 2. Численные методы Тема 1. Решение нелинейных уравнений с одной переменной 1.1. Постановка задачи При решении ряда задач физики, механики и техники возникает необходимость решения уравнений с одной переменной. В общем случае нелинейное уравнение можно записать в виде: F(x)=0, где функция F(x) определена и непрерывна на промежутке {a, b}.
Приближённое решение алгебраических и трансцендентных уравнений
Приближённое решение алгебраических и трансцендентных уравнений 1. Общая постановка задачи. Найти действительные корни уравнения , где - алгебраическая или трансцендентная функция.
Нелинейное уравнение и интервал изоляции корня
Изучение методов уточнения корней нелинейных уравнений (половинного деления, хорд, касательных, простой итерации). Метод хорд и касательных дает высокую скорость сходимости при решении уравнений, и небольшую - метод половинного деления и простой итерации.
Нахождение корня нелинейного уравнения. Методы решения системы нелинейных уравнений
Приближенные значения корней. Метод дихотомии (или деление отрезка пополам), простой итерации и Ньютона. Метод деления отрезка пополам для решения уравнения. Исследование сходимости метода Ньютона. Построение нескольких последовательных приближений.
Решение одного нелинейного уравнения
Методы решения одного нелинейного уравнения: половинного деления, простой итерации, Ньютона, секущих. Код программы решения перечисленных методов на языке программирования Microsoft Visual C++ 6.0. Применение методов к конкретной задаче и анализ решений.
Нахождение всех действительных корней алгебраического многочлена методом деления отрезка пополам (бисекции)
В данной курсовой работе рассмотрен принцип нахождения корней алгебраического многочлена следующими численными методами: метод бисекции, метод хорд и касательных, метод разложения на множители с учетом определяемой точности.
Приближенное вычисление корней в уравнения
Приближённое решение уравнений: метод хорд, метод касательных, комбинированный способ.
Приближенное решение уравнений методом хорд и касательных
Магнитогорский государственный технический университет Приближенное решение уравнений методом хорд и касательных Подготовил: Григоренко М.В. Студент группы ФГК-98
Решение нелинейных уравнений
Графическое решение нелинейного уравнения. Уточнение значение одного из действительных решений уравнения методами половинного деления, Ньютона–Рафсона, секущих, простой итерации, хорд и касательных, конечно-разностным и комбинированным методом Ньютона.
Метод касательных решения нелинейных уравнений
Определение корней нелинейного уравнения методом касательных аналитически и численным методом.