Название: Вычисления по теории вероятностей

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 136.31 Kb

Скачать файл: referat.me-217705.docx

Краткое описание работы: Применение классического определения вероятности в решении экономических задач. Определение вероятности попадания на сборку бракованных и небракованных деталей. Вычисление вероятности и выборочного значения статистики при помощи формулы Бернулли.

Вычисления по теории вероятностей

Задача 1. В партии из 60 изделий 10 – бракованных. Определить вероятность того, что среди выбранных наудачу для проверки 5 изделий окажутся бракованными:

а) ровно 2 изделия;

б) не более 2 изделий.

Решение.

А)

Используя классическое определение вероятности:

Р(А) – вероятность события А, где А – событие, когда среди выбранных наудачу изделий для проверки 5 изделий окажутся бракованными ровно 2 изделия;

m – кол-во благоприятных исходов события А;

n – количество всех возможных исходов;

Б)

Р(А’) – вероятность события А’, где А’ – событие, когда среди выбранных наудачу изделий для проверки 5 изделий окажутся бракованными не более 2 изделий,

;

– кол-во благоприятных исходов события ;

– кол-во благоприятных исходов события ;

– кол-во благоприятных исходов события ;

n’ – количество всех возможных исходов;

Ответ: вероятность того, что среди выбранных наудачу для проверки 5 изделий окажутся бракованными: а) ровно 2 изделия равна 16%. б) не более 2 изделий равна 97%.

Задача 2. В сборочный цех завода поступают детали с трех автоматов. Первый автомат дает 1% брака, второй – 2%, третий – 3%. Определить вероятность попадания на сборку небракованной детали, если с каждого автомата в цех поступило соответственно 20, 10, 20 деталей.

Решение.

По формуле полной вероятности:

где А – взятие хорошей детали, – взятие детали из первого (второго / третьего) автомата, – вероятность взятия детали из первого (второго / третьего) автомата, – вероятность взятия хорошей детали из первого (второго / третьего) автомата, – вероятность попадания на сборку небракованной детали.

; (т. к. ) = 1% = 0.01)

;

;

Ответ: Вероятность попадания на сборку небракованной детали равна 98%.

Задача 3. В сборочный цех завода поступают детали с трех автоматов. Первый автомат дает 1% брака, второй – 2%, третий – 3%. С каждого автомата поступило на сборку соответственно 20, 10, 20 деталей. Взятая на сборку деталь оказалась бракованной. Найти вероятность того, что деталь поступила с 1-го автомата.

Решение.

По формуле полной вероятности:

где А’ – взятие бракованной детали, – взятие детали из первого (второго / третьего) автомата, – вероятность взятия детали из первого (второго / третьего) автомата, – вероятность взятия бракованной детали из первого (второго / третьего) автомата, – вероятность попадания на сборку бракованной детали.

; (согласно условию)

;

;

Согласно формуле Байеса:

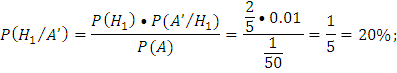
Ответ: Вероятность того, что деталь поступила с 1-го автомата равна 20%.

Задача 4. Рабочий обслуживает 18 станков. Вероятность выхода станка из строя за смену равна . Какова вероятность того, что рабочему придется ремонтировать 5 станков? Каково наивероятнейшее число станков, требующих ремонта за смену?

Решение.

Используя формулу Бернулли, вычислим, какова вероятность того, что рабочему придется ремонтировать 5 станков:

где n – кол-во станков, m – кол-во станков, которые придётся чинить, p – вероятность выхода станка из строя за смену, q =1-р – вероятность, не выхождения станка из строя за смену.

.

Ответ: Вероятность того, что рабочему придется ремонтировать 5 станков равна 15%. Наивероятнейшее число станков, требующих ремонта за смену равно 3.

Задача 5. В двух магазинах, продающих товары одного вида, товарооборот (в тыс. грн.) за 6 месяцев представлен в таблице. Можно ли считать, что товарооборот в первом магазине больше, чем во втором? Принять = 0,05.

Все промежуточные вычисления поместить в таблице.

Магазин №1	Магазин №2
20,35	20,01
20,60	23,55
32,94	25,36
37,56	30,68
40,01	35,34
25,45	23,20

Пусть, a₁ – товарооборот в 1 магазине, a₂ – товарооборот во 2 магазине.

Формулируем гипотезы Н₀ и Н₁ :

Н₀ : a₁ = a₂

Н₁ : a₁ ≠ a₂

	xi	xi-a1	(xi-a1)2	yi	yi-a2	(yi-a2)2
	20,35	-9,135	83,44823	20,01	-6,35	40,32
	20,6	-8,885	78,94323	23,55	-2,81	7,896
	32,94	3,455	11,93703	25,36	-1	1
	37,56	8,075	65,20563	30,68		18,66
	40,01	10,525	110,7756	35,34	4,32	80,64
	25,45	-4,035	16,28123	23,20	8,98	9,98
∑	176,91		366,591	158,14	-3,16	158,496

a₁ = = = 29,485, a₂ = =

₁ = = 73.32

₂ = =

n ₁ = n ₂ = n =6

Вычислю выборочное значение статистики:

Z_В = * =

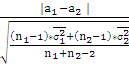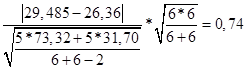
Пусть = 0,05. Определяем необходимый квантиль распределения Стьюдента: (n₁ +n₂ -2)= 2.228.

Следовательно, так как Z_В =0,74 < =2,228, то мы не станем отвергать гипотезу Н₀ , потому что это значит, что нет вероятности того, что товарооборот в первом магазине больше, чем во втором.

Задача 6. По данному статистическому ряду:

1. Построить гистограмму частот.

2. Сформулировать гипотезу о виде распределения.

3. Найти оценки параметров распределения.

4. На уровне значимости = 0,05 проверить гипотезу о распределении случайной величины.

Все промежуточные вычисления помещать в соответствующие таблицы.

Интервал	Частота случайной величины
1 – 2	5
2 – 3	8
3 – 4	19
4 – 5	42
5 – 6	68
6 -7	44
7 – 8	21
8 – 9	9
9 – 10	4

1. Гистограмма частот:

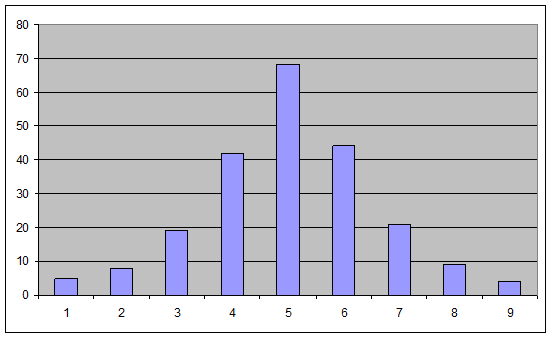
2. Предположим, что моя выборка статистического ряда имеет нормальное распределение.

3. Для оценки параметров распределения произведем предварительные расчеты, занесем их в таблицу:

№	Интервалы	Частота, mi	Середина Интервала, xi	xi *mi	xi 2 *mi
1	1–2	5	4,5	7,5	112,5
2	2–3	8	2,5	20	50
3	3–4	19	3,5	66,5	232,75
4	4–5	42	4,5	189	350,5
5	5–6	68	5,5	374	2057
6	6–7	44	6,5	286	1859
7	7–8	21	7,5	157,5	1181,25
8	8–9	9	8,5	76,5	650,25
9	9–10	4	9,5	38	361
∑		n=220		1215	7354,25

Найдем оценки параметров распределения:

= = 5,523

² = ² = 2,925 = = 1,71

4. все вычисления для проверки гипотезы о распределении занесем в таблицы.

№	Интервалы	Частоты, mi	t1	t2	Ф(t1 )	Ф(t2 )	pi
1	-∞ – 2	5	-∞	-2,06	0	0,0197	0,0197
2	2–3	8	-2,06	-1,47	0,0197	0,0708	0,0511
3	3–4	19	-1,47	-0,89	0,0708	0,1867	0,1159
4	4–5	42	-0,89	-0,31	0,1867	0,3783	0,1916
5	5–6	68	-0,31	0,28	0,3783	0,6103	0,232
6	6–7	44	0,28	0,86	0,6103	0,8051	0,1948
7	7–8	21	0,86	1,45	0,8051	0,9265	0,1214
8	8–9	9	1,45	2,03	0,9265	0,9788	0,0523
9	9-∞	4	2,03	∞	0,9788	1	0,0212

Где: t₁ = , t_{2 =} , a_i , b_i – границы интервала, Ф(t) – Функция распределения нормального закона.

p_i = Ф(t₂ ) – Ф(t₁ )

Так как проверка гипотезы о распределении производится по критерию , составляем еще одну таблицу для вычислений:

№ интервала	pi	mi	n* pi
1 2	0,0708	13	15,57	0,4242
3	0,1159	19	25,5	1,6569
4	0,1916	42	42,15	0,0005
5	0,232	68	51,04	5,6336
6	0,1948	44	42,86	0,0303
7	0,1214	21	26,71	1,2207
8 9	0,0735	13	16,17	0,6214
∑				9,5876

Согласно расчетам, = = 9,5876

Выбираем уровень значимости = 0,05 и вычисляем _1-α (k-r-1), где k – число подмножеств, r – число параметров в распределении.

_0,95 (7–2–1) = _0,95 (4) = 9,49.

Сравнив полученное значение с расчетным можно сделать вывод, что так как расчетное значение больше, следовательно, гипотеза о нормальном распределении выборки статистического ряда не принимается.

Задача 7. По данным выборки вычислить:

а) выборочное значение коэффициента корреляции;

б) на уровне значимости = 0,05 проверить гипотезу о значимости коэффициента корреляции.

Решение

Формулируем гипотезы Н₀ и Н₁ :

Н₀ : a₁ = a₂

Н₁ : a₁ ≠ a₂

	xi	xi-a1	(xi-a1)2	yi	yi-a2	(yi-а2)2	xi*yi
	4,40	-0,476	0,2266	3,27	-0,47	0,2209	14,388
	5,08	0,204	0,0416	4,15	0,41	0,1681	21,082
	4,01	-0,866	0,7499	2,95	-0,79	0,6241	11,829
	3,61	-1,266	1,6027	1,96	-1,78	3,1684	7,075
	6,49	1,614	2,605	5,78	2,04	4,1616	37,512
	4,23	-0,646	0,4173	3,06	-0,68	0,4824	12,944
	5,79	0,914	0,8354	4,45	0,71	0,5041	25,765
	5,52	0,644	0,4147	4,23	0,49	0,2401	23,349
	4,68	-0,196	0,0384	3,54	-0,2	0,04	16,567
	4,95	0,074	0,0055	4,01	0,27	0,0729	19,849
∑	48,76	-	6,9371	37,4	-	9,6626	190,36

a₁ = = 4,876, a₂ = = 3,74

₁ = = 0,7708

₂ = = 1,0736

n ₁ = n ₂ = n =6

а) Вычислим выборочное значение коэффициента корреляции

=

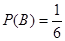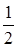
б) Проверим на уровне значимости =0,05 гипотезу о значимости коэффициента корреляции:

(n-2)=2,306

Вычислим величину

=

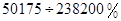получаем, что >0.6319 т.е. попадает в критическую область, следовательно, коэффициент корреляции можно считать значимым.

Задача 8. По данным выборки найти:

а) точечные оценки математического ожидания и дисперсии;

б) с доверительной вероятностью р =1- найти доверительные интервалы для математического ожидания и дисперсии.

α	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
0.01	3,85	8,87	21,26	6,72	0,29	15,48	7,48	0,33	0,34	1,37

Решение

а) Вычислим математическое ожидание и дисперсию. Промежуточные значения поместим в таблицу.

xi	mi	mi xi	mi xi 2
3,85	1	3,85	14,822
8,87	1	8,87	78,677
21,26	1	21,26	451,987
6,72	1	6,72	45,158
0,29	1	0,29	0,0840
15,48	1	15,48	239,630
7,48	1	7,48	55,950
0,33	1	0,33	0,109
0,34	1	0,34	0,115
1,37	1	1,37	1,877
∑65,99	10	65,99	888,409

Математическое ожидание:

m==

Дисперсия:

δ2==

б) с доверительной вероятностью р =1- найти доверительные интервалы для математического ожидания и дисперсии, считая, что выборка получена из нормальной совокупности.

Определим из таблиц значение , где ;

Доверительный интервал для математического ожидания имеет вид:

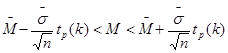
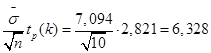
Подставив полученные значения, найдем доверительный интервал для математического ожидания:

0,271<M<12.927

Доверительный интервал для дисперсии имеет вид:

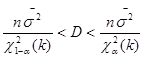
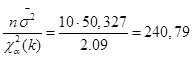
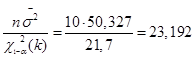
Доверительный интервал для дисперсии равен: 23,192<D<240,79.