Название: Теория вероятности

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 85.36 Kb

Скачать файл: referat.me-217779.docx

Краткое описание работы: Определение числа исходов, благоприятствующих данному событию. Теорема умножения вероятностей и сложения несовместных событий, локальная теорема Лапласа. Расчет среднеквадратического отклонения величин. Несмещенная оценка генеральной средней и дисперсии.

Теория вероятности

КОНТРОЛЬНАЯ РАБОТА

на тему «Теория вероятности »

по предмету «Математика»

Задание 1

Общее число возможных элементарных методов равно числу сочетаний из 10 по 5:

.

Подсчитываем число исходов, благоприятствующих нашему событию. Среди 3-х женщин две женщины могут быть выбраны способами; при этом остальные 5–2=3 людей должны быть мужчинами. Взять же 3 мужчины из 7 можно способами. Следовательно, число исходов благоприятствующих нашему событию:

.

Искомая вероятность равна:

.

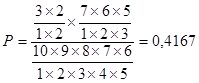Задание 2

.

Возможны следующие три случая:

А – среди трех студентов посетивших библиотеку первый заказал учебник по теории вероятностей, а два других не заказали;

В – второй студент заказал учебник по теории вероятностей, а первый и второй нет.

Вероятность каждого из этих событий по теореме умножения равны:

;

;

.

Искомая вероятность по теореме сложения несовместных событий:

.

Поэтому: .

Чтобы нити оказались одного цвета должны выполниться следующие события:

А – вынуть две нити красного цвета;

В – вынуть две нити белого цвета.

Вероятность каждого из этих событий по теореме умножения вероятностей будут:

;

.

Искомая вероятность по теореме сложения вероятностей: .

Задание 3

.

I – 4б; 6кр; II – 5б; 10кр

Обозначим события А – выбранный шар белый. Можно сделать два предложения:

– белый шар выбран из 1-го ящика

– белый шар выбран из 2-го ящика, так как ящик выбирают на удачу, то:

.

Условная вероятность того, что шар будет белым и извлечен он из первого ящика будет:

.

Вероятность того, что белый шар будет извлечен из второго ящика:

.

Формула полной вероятности:

.

Тогда вероятность того, что наугад взятый шар будет белым:

.

Задание 4

Воспользуемся локальной теоремой Лапласа:

;

;

.

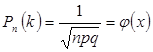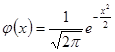В нашем случае n=600; k=25; P=0,05; q=0,95.

.

Так как функция – четная, то по таблице находим:

.

Тогда .

Задание 5

x	20	25	30	35	40
P	0,2	0,3	0,2	0,1	0,2

.

;

;

;

.

Начальный момент первого порядка: .

Аналогично: .

.

Находим центральные моменты по формулам:

;

;

.

Следовательно:

; ; .

Многоугольник распределения

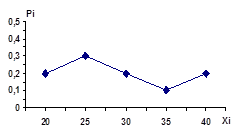
Задание 6

Распределение Х и распределение Y

Xi	4	9	12	Yi	6	7
Pi	0,36	0,24	0,4	Pi	0,65	0,35

;

.

;

;

;

;

;

.

Коэффициент коррекции находим по формуле:

,

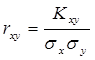где: K_xy – корелляционный момент связи случайных величин X и Y; – среднеквадратические отклонения величин X и Y.

.

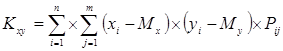Тогда:

;

;

.

.

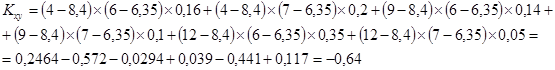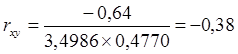Задание 7

; .

;

.

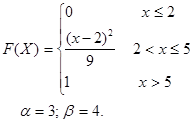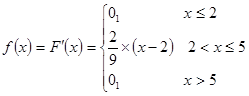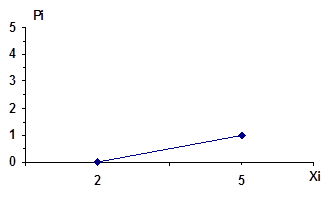
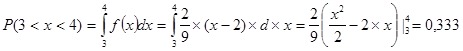Задание 8

Распределение Х и распределение Y

Xi	1	3	5	Yi	12	13	15
Pi	0,1	0,7	0,2	Pi	0,5	0,1	0,4

x₁ =1; x₂ =3; x₃ =5; y₁ =12; y₂ =13; y₃ =15; x₁ + y₁ =13; x₁ + y₂ =14; x₁ + y₃ =16;

x₂ + y₁ =15; x₂ + y₂ =16; x₂ + y₃ =18; x₃ + y₁ =17; x₃ + y₂ =18; x₃ + y₃ =20;

Обозначим x_i + y_j =7, тогда имеем следующие значения z:

z₁ =13; z₂ =14; z₃ =15; z₄ =16; z₅ =17; z₆ =18; z₇ =20.

Соответствующие вероятности будут:

;

;

;

;

;

;

.

Искомое распределение

x+y	13	14	15	16	17	18	20
P	0,04	0,06	0,12	0,28	0,04	0,36	0,10

Контроль:

0,04+0,06+0,12+0,28+0,04+0,36+0,1=1.

Задание 9

Xi	2	4	6	8	10	12	14	16
ni	1	2	3	4	5	10	6	5

Находим значение эмпирической функции.

Вычисления выполняем в таблице.

Таблица вычислений

Xi	2	4	6	8	10	12	14	16
Частота	0,028	0,056	0,083	0,111	0,139	0,278	0,166	0,139
	0,028	0,084	0,167	0,278	0,417	0,695	0,861	1,00

График эмпирической функции

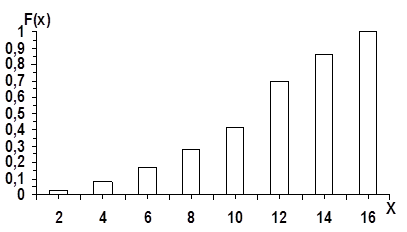
Несмещенной оценкой генеральной средней является выборочная средняя:

.

Тогда:

.

Несмещенную оценку генеральной дисперсии найдем по формуле:

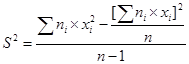
Последовательно находим:

;

;

;

.

Модой называют варианту, имеющую наибольшую частоту.

.

Медиана:

.

Размах варьирования:

R=16–2=14.

Из соотношения находим и t=1,96.

Находим точность оценки по формуле:

.

Тогда:

.

Доверительный интервал таков: ().