Название: Аппроксимация экспериментальных зависимостей

Вид работы: курсовая работа

Рубрика: Математика

Размер файла: 99.21 Kb

Скачать файл: referat.me-217782.docx

Краткое описание работы: Аппроксимация экспериментальных зависимостей методом наименьших квадратов. Правило Крамера. Графическое отображение точек экспериментальных данных. Аномалии и допустимые значения исходных данных. Листинг программы на С++. Результаты выполнения задания.

Аппроксимация экспериментальных зависимостей

Задание 1

Данные давления водорода Н₂ на линии насыщения приведены в таблице. Сделать аппроксимацию экспериментальных данных в виде степенной функции и многочлена первой степени. Произвести сравнительный анализ ошибки аппроксимации полученной двумя функциями.

Таблица 1

Ts ,0 К	32	33	34	35	36	37	38	39
Pмм рт. ст.	360,3	509,5	699,2	935,3	1223.7	1570,5	1981,8	2463,8

Аппроксимация экспериментальных зависимостей методом наименьших квадратов. Теоретические сведения

Пусть, в результате эксперимента получена зависимость.

Необходимо найти аналитическую формулу f = , которая аппроксимирует экспериментальную (табличную) зависимость.

Выберем зависимость в виде полинома 2 – й степени, т.е.

(1)

В выражении (1) коэффициенты , , подлежат определению, причем эти коэффициенты должны быть подобраны таким образом, чтобы зависимость наилучшим образом приближалась к экспериментальной зависимости. Пусть отклонение - различие между табличным значением в точке и значением аналитической функции в этой же самой точке, т.е.:

(2)

В соответствии с методом наименьших квадратов (МНК) наилучшими коэффициентами зависимости (1) будут такие, для которых сумма квадратов отклонений будет минимальной.

(3)

Используя необходимые условия существования экстремума для функций нескольких переменных , находим уравнение для определения коэффициентов зависимости (1).

(4)

Из условия (4) получим систему линейных алгебраических уравнений:

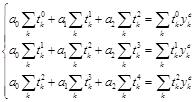(5)

Решив систему (5) найдем коэффициенты аппроксимирующей зависимости (1).

Эффективным методом решения систем линейных алгебраических уравнений является матричный метод. Сущность его состоит в следующем.

Пусть А — матрица коэффициентов системы уравнений, X — вектор неизвестных, В — вектор правых частей системы уравнений. Тогда решение системы уравнений в матричной форме будет иметь вид:

Х = А ^-1 В.

Правило Крамера

Если ранг матрицы совместной системы равен числу ее неизвестных, то система является определенной. Если число неизвестных системы совпадает с числом уравнений ( m = n ) и матрица системы невырожденная (detA ≠ 0), то система имеет единственное решение, которое находится по правилу Крамера:

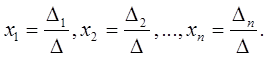
В этих формулах ∆ = detА — определитель системы, а ∆_k — определитель, полученный из определителя системы заменой k -г o столбца столбцом свободных членов ( k = 1, 2,..., n ).

Решение системы трех линейных уравнений с тремя неизвестными можно выразить через определители:

, ,

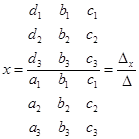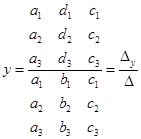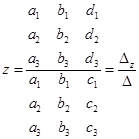
Информационное обеспечение

Зависимость давления P водорода Н₂ при различных температурах на линии насыщения приведены в таблице (1).

Для проведения анализа исходных данных с целью выбора вида аппроксимирующего многочлена построим график функции, заданной в табл.1. График приведен на рис.1.

Графическое отображение точек экспериментальных данных

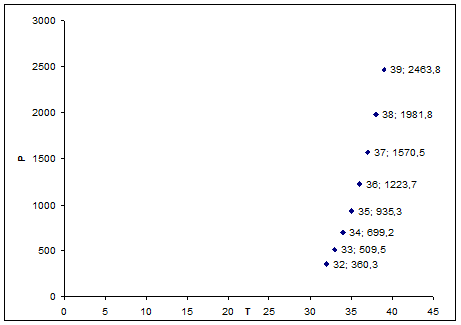
Рис. 1.Экспериментальная зависимость P=f(T)

В результате анализа данных выберем в качестве аппроксимирующего многочлена параболу, заданную уравнением P₂ (x)=a₀ +a₁ x+a₂ x² .

Для определения коэффициентов a₀ , a₁ , a₂ запишем систему уравнений вида

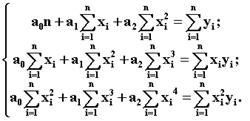
При составлении системы создадим вспомогательную таблицу данных (таблица 2).

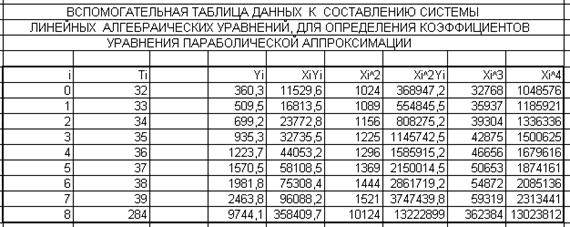
Используя данные таблицы 2, систему уравнений (5) записываем в виде

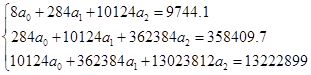
В результате решения системы методом Крамера получаем следующие значения определителей:

detA = 56448;

detA1 = 1435933397;

detA2 = -94279012,8;

detA3 = 1564382,4;

Вычислив определители, рассчитываем значения коэффициентов:

a₀ = detA1/ detA;

a₁ = detA2/detA;

a₂ = detA3/ detA;

a₀ = 25438,1625;

a₁ = -1670,19226;

a₂ = 27,71369048.

Таким образом, искомый аппроксимирующий многочлен имеет вид:

(6)

Полученная аналитическая зависимость (6) обобщает экспериментальные данные табл.01.

Для оценки погрешности полученной зависимости составим таблицу значений P. Для этого определим давление P по формуле (6). Результаты внесем в таблицу 2.

Таблица 2

T	32	33	34	35	36	37	38	39
P	370,8291668	502,0267858	688,6518	930,7042	1228,1839	1581,091	1989,4256	2453,188

Для оценки точности параболической аппроксимации сравниваем значения Р из табл.01 и табл.2. Модуль разности соответствующих значений представляет DP-погрешность аппроксимации, значения которой представлены в табл.3. В таблице приведена также относительная погрешность dР, равная отношению DР к Р.

Таблица 3

Т	32	33	34	35	36	37	38	39
DР	10,529	7,4732	0,5482	4,59583	4,4839	10,591	7,625	10,6125
dP,%	2,8393578	1,4886087	1,5317	0,4938	0,36509	0,6699	0,38331	0,4326

Сравнительный анализ погрешностей показывает, что полученная аналитическая зависимость удовлетворительно обобщает исходные экспериментальные данные.

Для интегральной оценки аппроксимации можно использовать формулу:

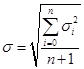
На рис. 2 приведены два графика, один из которых построен по данным аппроксимации (табл. 2), а второй - по исходным данным (табл.01).

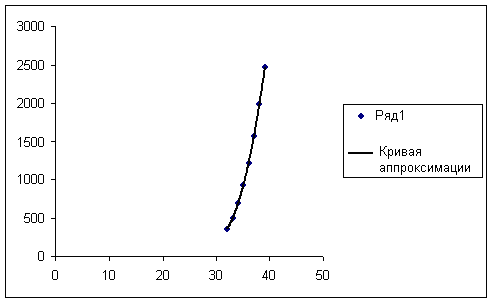
Сравнивая эти графики, можно также отметить удовлетворительную сходимость теоретических и экспериментальных данных.

Выберем в качестве аппроксимирующего многочлена линейную функцию.

Аппроксимируем данную табличную зависимость многочленом первой степени P₁ (x)=a₀ +a₁ x

Для определения коэффициентов а₀ , а₁ необходимо составить систему уравнений

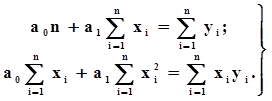
Подставив данные таблицы в систему уравнений получим:

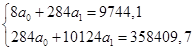
Находим а₀ и а₁ методом Крамера:

а₀ = -9343,52, а₁ = 297,4798

Следовательно, искомый аппроксимирующий многочлен имеет вид

P= ─ 9342,52 + 297,4798T(7)

Формула (7) является аналитической зависимостью, обобщающей экспериментальные данные табл. 01.

Для оценки линейной аппроксимации необходимо сравнить значения y_i из табл. 4 со значениями, полученными по формуле (7) для всех точек (i=1, 2, ..., 8). Результаты сравнения представлены в таблице 5.

Таблица 5

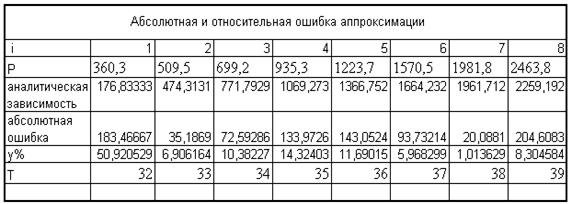
Проанализировав табл.5 можно сделать вывод, формула (7) не является корректной аналитической зависимостью, обобщающей экспериментальные данные табл. 01.

На рис.3 приведены график функции (7) и исходные экспериментальные данные. Сравнительный анализ показывает неудовлетворительную сходимость теоретических и экспериментальных данных.

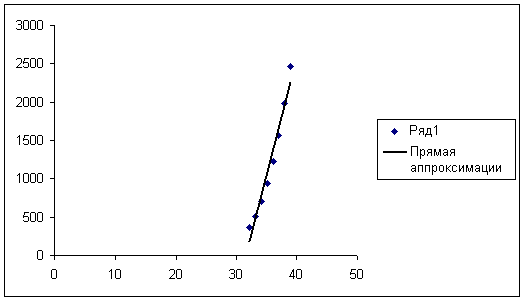
Рис.5.3. График линейного аппроксимирующего многочлена и исходные данные.

Текст программы

#include<iostream.h>

#include<math.h>

#include<conio.h>

#include<graphics.h>

#include<stdio.h>

#define PATHTODRIVER "c:egavga.bgi"

void GrafikPolinom(float, float, float, float, float, float );//Функция //построенияграфикаполиномиальнойаппроксимацииэкспериментальныхданных

void GrafikLinear(float,float,float,float,float);//Функцияпостроения

//графика линейной аппроксимации экспериментальных данных

voidGRAPH_POINTS(float,float,float,float ); //Функция выводит на экран точки //экспериментальных данных

int GRAPH_MODE(); //Функция инициализации графического режима

voidGRID(float, float);// Функция формирования координатной сетки

/*-------------------------------------------------------------------------*/

int main()

{ clrscr();

int n;

floattmpr,pwr; //текущие значения аргумента и функции

floatdiscret; //дискретность изменения аргумента

floattn0, tn; //диапазон изменения аргумента tn0 - min, tn - max

float pn; //pn-max экспериментальное значение функции

float *dp = new float [n]; //Массив значений ошибок аппроксимации

float *P = new float [n]; //Массив значений //полученный аналитическим способом

float INTG = 0; //переменная, используемая в выражении //интегральной оценки аппроксимации

float A = 0, B = 0, C = 0, D = 0, E = 0, F = 0, G = 0;

float detA,i, detA1, detA2, detA3, A0,A2,A3;

int answer;

Вводзначенийэкспериментальныхданных*/ cout<<" Input number double values "<<endl;

cin>>n;

cout << " ENTER ARGUMENT VALUE " << endl;

float *t = new float [n]; //Массив значений аргумента (в данном случае - температура)

float *p = new float [n]; //Массив значений функции исследуемого процесса for( i=0;i<n;i++) {cout<<"EnterT"<<(i+1)<<"="; cin>>t[i]; }

cout <<" ENTER EXPERIMENTAL FNCTION VALUE"<<endl; for(i=0;i<n;i++) {cout<<"Enter P"<<(i+1)<<"="; cin>>p[i]; }

L:

cout <<" FOR DRAWING POINTS PRESS <1>n" ;

cout <<" FOR FIND APROCSIMATION POLINOM FUNCTION INPUT <2>n" ;

cout <<" FOR FIND APROCSIMATION LINEAR FUNCTION INPUT <4>n" ;

cout <<" FOR FIND DRAWING POLINOM FUNCTION INPUT <3>n" ;

cout <<" FOR FIND DRAWING LINEAR FUNCTION INPUT <5>n" ;

cout <<" FOR EXIST INPUT <0>n" ;

cin>>answer;

/* Графическое отображение экспериментальных данных в виде точек зависимости P = f(t) на координатной плоскости */

if (answer ==1)

{

int regimen = GRAPH_MODE();

if(regimen == 5)

{ tn0 = t[0]; tn = t[n-1];//tn-max экспериментальное значение температуры (аргумента) pn = p[n-1];//pn-max экспериментальное значение функции

GRID(tn,pn);

for(i = 0;i<n;i++)

{

tmpr= t[i];

pwr = p[i];

setbkcolor(1);

GRAPH_POINTS( tn,pn,tmpr,pwr );

} getch () ; closegraph(); // выход из графического режима

}

else

{ cout<<" Error code regimen = "<<regimen<<endl; getch(); closegraph();

} gotoL;

}

/* Расчет функции аппроксимации экспериментальных данных в виде полинома 2 - й степени */

if(answer ==2) { for( i=0;i<n;i++) { A = A + t[i]; B = B + p[i]; C = C + t[i]*p[i]; D = D + t[i]*t[i]; E = E + t[i]*t[i]*p[i]; F = F + t[i]*t[i]*t[i]; G = G + t[i]*t[i]*t[i]*t[i]; } //

cout<<"A = "<<A<<" B = "<<B<<endl; //

cout<<"C = "<<C<<" D = "<<D<<endl; //

cout<<"E = "<<E<<" F = "<<F<<endl; //

cout<<"G = "<<G<<endl; /*n,A,B,C,D,E,F,G - коэффициентымногочленовдлясистемыуравненийвида: n*(a0) + A*(a1) + D*(a2) = B A*(a0) + D*(a1) + F*(a2) = C D*(a0) + F*(a1) + G*(a2) = E */ // РешаемсистемуметодомКрамераdetA = n*D*G + A*F*D + D*A*F - D*D*D - A*A*G - n*F*F; detA1 = B*D*G + C*F*D + E*A*F - E*D*D - C*A*G - B*F*F; detA2 = n*C*G + A*E*D + D*B*F - D*C*D - A*B*G - E*F*n; detA3 = n*D*E + A*F*B + D*A*C - D*D*B - A*A*E - F*C*n; // cout << " detA = " << detA << " detA1 = " << detA1 << endl; // cout << " detA2 = " << detA2 << " detA3 = " << detA3 << endl; cout << " A0 = " << (A0 = detA1/detA) << endl; cout << " A2 = " << (A2 = detA2/detA) << endl; cout << " A3 = " << (A3 = detA3/detA) << endl;

cout << "APROCSIMATION POLINOM:" << endl; A2=A2; A3 = A3; cout << "P = (" << A0<<")+(" << (A2) << ")*T + (" << (A3) << ")*T^2" <<endl; for ( i=0; i<n; i++) { P[i] = A0 + A2*t[i] + A3*t[i]*t[i]; cout<<"P["<<i<<"]="<<P[i]<<" "; } cout<<"n";

cout << " THE ABSOLUTE & RELATIVE MISTAKES OF APROCTIMATION n"; for ( i=0; i<n; i++) { dp[i] = (P[i]-p[i]); cout<< "dP["<<i<<"]="<<(fabs(dp[i]))<<" dP(%)="<<(100*fabs(dp[i])/p[i])<<endl; }

cout <<" INTEGRAL LEVEL OF APROCTIMATION IS:n" ;

for ( i=0; i<n; i++) { INTG = INTG + (dp[i])*dp[i]; } float ITG = sqrt(INTG/(n+1)); cout<<"ITG = "<<ITG<<"n"; //интегральнаяоценкааппроксимацииgetch();

goto L; }

/* Графическое отображение, полученной зависимости P = f(t) в виде полинома 2 степени, на координатной плоскости */

if(answer == 3) {

int regimen = GRAPH_MODE();

if(regimen == 5)

{ tn0 = t[0]; tn = t[n-1];//tn-max экспериментальное значение температуры (аргумента) pn = p[n-1];//pn-max экспериментальное значение функции

GRID(tn,pn);

setbkcolor(1);

GrafikPolinom(A0, A2, A3,tn0,tn,pn );

for(i = 0;i<n;i++)

{

tmpr= t[i];

pwr = p[i];

GRAPH_POINTS( tn,pn,tmpr,pwr );

} getch () ; closegraph(); // выход из графического режима

}

else

{ cout<<" Error code regimen = "<<regimen<<endl; cout << "Dont find driver or driver damagedn" ; /*Вэтомместе cделатьвозвратвглавноеменю*/ getch(); closegraph();

}

goto L;

}

/*-------------------------------------------------------------------------*/ /* Расчет линейной функции аппроксимации экспериментальных данных */ cout<<" II. LINEARAPROCTIMATION " <<endl; floatR = 0, R2 = 0, B0, B1; floatSCp = 0, Cpi = 0, detB, detB1, detB2; float* dCp = newfloat [n];; float* ACp = newfloat [n];; floatINTGL = 0; if(answer == 4) { for ( i=0;i<n;i++) { R = R+t[i]; SCp = SCp + p[i]; R2 = R2 + t[i]*t[i]; Cpi = Cpi + p[i]*t[i]; } // cout << " R =" << R << " SCp =" << SCp << endl; // cout << " R2 =" << R2 << " Cpi =" << Cpi << endl; /*n, R, SCp, R2, Cpi - коэффициенты в уравнениях для системы вида (А0)*n + (A1)*R= SCp(A0)*R + (A1)*R2 = Cpi*/ detB = n*R2 - R*R; detB1 = SCp*R2 - R*Cpi; detB2 = n*Cpi - R*SCp; // cout<<"detB = "<<detB<<" detB1 = "<<detB1<<"detB2 = "<<detB2<<"n"; B0 = detB1/detB; B1 = detB2/detB; // cout << " B0 =" << B0 << endl; // cout << " B1 =" << B1 << endl; cout << " APROCTIMATIONLINEARPOLINOM" << endl; cout<<"F =("<<B0<<") + ("<<B1<<")*T" << endl; for (i = 0; i<n;i++) { ACp[i] = B0 + B1* t[i]; cout <<"ACp["<<i<<"]=" <<ACp[i]<<endl; } for ( i = 0; i<n;i++) { dCp[i] = ACp[i] - p[i]; cout<< "dCp["<<i<<"]="<<(fabs(dCp[i]))<<" dCp(%)="<<(100*fabs(dCp[i])/p[i])<<endl; } cout <<" INTEGRALLEVELOFAPROCTIMATIONIS:n" ; for ( i=0; i<n; i++) { INTGL = INTGL + (dCp[i])*(dCp[i]); } floatITGL = sqrt(INTGL/(n+1)); cout<<"ITGL = "<<ITGL<<"n"; cout<<" "<<"n"; getch(); goto L; }

Графическое отображение, полученной зависимости P = f(t) в виде линейной функции аппроксимации на, координатной плоскости */

if(answer==5)

{

int regimen = GRAPH_MODE();

if(regimen == 5)

{ tn0 = t[0]; tn = t[n-1]; tn = t[n-1]; pn = p[n-1]; GRID(tn,pn);

setbkcolor(1);

GrafikLinear( B0,B1,tn0,tn,pn );

for(i=0;i<n;i++)

{tmpr = t[i]; pwr = p[i]; GRAPH_POINTS(tn,pn,tmpr,pwr);

} getch () ; closegraph(); // выход из графического режима

}

else

{ cout << " Error code regimen = "<<regimen<<endl; cout << "Dont find driver or driver damagedn" ; getch();

} goto L;

}

return 0;

}

* Функция вывода на координатную плоскость графика функции 2-й степени */

void GrafikPolinom (float A0, float A2, float A3,float tn0,float tn, float pn )

{

float x,dx; // аргумент и его приращение

float xl,x2; // диапазон изменения аргумента

float y; // значение функции

float mx,my; // масштаб по X и Y - кол-во точек экрана, соответствующих // единице по осям координат

int x0,y0; // начало осей координат

float px,py; // координаты точки графика на экране

x0 = 50;

y0 = 400;

mx = 630/(2*tn);

my = 470/(2*pn);

// осикоординат

line(10,y0,630,y0);

line(x0,10,x0,470);

// график

xl = tn0;

x2 = tn;

dx = 0.01;

x = xl;

while ( x < x2 )

{

y =A3*x*x + A2*x+A0; // функция

px = x0 + x*mx;

py = y0 - y*my;

putpixel(px,py, WHITE);

x += dx;

}}

int GRAPH_MODE()

{

int grdriver = DETECT; // драйвер

int grmode; // режим

int errorcode; // кодошибки

initgraph(&grdriver, &grmode, PATHTODRIVER);

errorcode = graphresult();

if (errorcode != grOk) // ошибка инициализации графического режима

{

printf("ERROR: dont find driver or driver damaged n", errorcode);

puts("PRESS <Enter>");

getch();

return(-10);

}

else

{ return(5);

}}

/* Функциявыводанакоординатнуюплоскостьграфикалинейнойфункции*/ void GrafikLinear (float B0, float B1,float tn0, float tn, float pn ) {

float x,dx; // аргумент и его приращение

float xl,x2; // диапазон изменения аргумента

float y; // значение функции

float mx,my; // масштаб по X и Y - кол-во точек экрана, соответствующих // единице по осям координат

int x0,y0; // начало осей координат

float px,py; // координаты точки графика на экране

x0 = 50;

y0 = 400;

mx = 630/(2*tn);

my = 470/(2*pn);

// осикоординат

line(10,y0,630,y0);

line(x0,10,x0,470);

// график

xl = tn0;

x2 = tn;

dx = 0.01;

x = xl;

while ( x < x2 )

{

y = B1*x+B0; // линейная функция

px = x0 + x*mx;

py = y0 - y*my;

putpixel(px,py, WHITE);

x += dx;

}}

/* Функциявыводаточекэкспериментальнойзависимостинаэкран*/ void GRAPH_POINTS( float tn,float pn,float tmpr,float pwr )

{

float x; // аргумент

float y; // значение функции

float mx,my; // масштаб по X и Y - кол-во точек экрана, соответствующее // единице по осям координат

int x0 = 50;

int y0 = 400;

mx = 630/(2*tn); //tn-max экспериментальное значение температуры (аргумента)

my = 470/(2*pn); //pn-max экспериментальное значение функции

y = y0 - pwr*my ;

x = x0 + tmpr*mx ;

setcolor(13);

circle(x,y,2);

}

/* ФункцияформированиякоординатнойсеткиирасчетамасштабапоX иY*/ void GRID (float tn, float pn)

{

int x0,y0; // координаты начала координатных осей

int dx,dy; // шаг координатной сетки (в пикселях)

int h,w; // высота и ширина области вывода координатной сетки int x,y;

float lx,ly; float dlx,dly; char st [8];

// метки линий сетки по X и Y

// шаг меток линий сетки по X и Y

// изображение метки линии сетки

x0 = 50; y0 = 400; // оси начинаются в точке (50,400)

dx = 40; dy = 40; // шаг координатной сетки 40 пикселей

dlx =1; // шаг меток оси X метками будут: 1, 2, 3 ...

dly =1; // шаг меток оси Y метками будут: 1, 2, 3 ...

h = 360; w = 560;

lx = 0; ly =0; //в начало координат ставятся метки 0

cout<<" MX = 1 : "<< 2*tn/14 <<"n"; //масштаб по Х

cout<<" MY = 1 : "<< 2*pn/9 <<"n"; //масштабпо Y

// засечки, сетка и оцифровка

int x = x0;

do

{

// засечка

sprintf(st,"%2.1f",lx);

outtextxy(x-8,y0+5,st);

lx += dlx;

// линиясетки

setlinestyle (DOTTED_LINE, 0, 1);

line(x,y0-3,x,y0-h);

x += dx; } while (x < x0+w);

// засечки, сетка и оцифровка по оси Y

int y = y0;

do

{

// оцифровка

sprintf(st,"%2.1f",ly) ;

outtextxy(x0-40,y, st) ;

ly += dly;

// линиясетки

setlinestyle(DOTTED_LINE, 0, 1);

line(x0+3,y,x0+w,y) ;

setlinestyle(SOLID_LINE, 0, 1);

y -= dy; } while (y > y0-h);

} ;

Результаты тестирования

Для проверки правильности вычисления аналитической формулы 2 – й степени, которая аппроксимирует экспериментальную (табличную), зависимость, выведем на экран:

- значения определителей [detA , detA 1, detA 2, detA 3 ] полученных при решении системы линейных уравнений и значения коэффициентов [A 0, A 2, A 3 ] в аналитической формуле, рассчитанные программой при выборе аппроксимирующего многочлена 2 – й степени;

- вспомогательные данные [A , B , C , D , E , F , G ] необходимые для вычисления уравнения функции аппроксимации экспериментальных данных 2 – й степени;

При тестировании получены следующие величины вышеперечисленных значений:

A = 284;

B = 97744,099609;

C = 358409,6875;

D = 10124;

E =13222899;

F = 362384;

G = 13023812;

detA = 56448;

detA 1 = 1,436059 *10⁹ ;

detA 2 = ─ 9,42861 * 10⁷ ;

detA3 = 1564482,25;

A0 = 25440,380859;

A1 = ─1670,317871;

A 2 = 27,71546;

Аппроксимирующий полином:

P = 25440,380859 ─ 1670,317871* T + 27,71546* T ² ;

Данная аналитическая зависимость, обобщает экспериментальные данные табл. 01.

Для проверки правильности вычисления аналитической формулы 1 – й степени, которая аппроксимирует экспериментальную (табличную), зависимость, выведем на экран:

- значения определителей [det В, det В1, det В2 ] полученные при решении системы линейных уравнений и значения коэффициентов [В0, В1 ] в аналитической формуле, рассчитанные программой при выборе аппроксимирующего многочлена 1 – й степени;

- вспомогательные данные [ R , SCp , R 2, Cpi ] необходимые для вычисления уравнения функции аппроксимации экспериментальных данных 1 – й степени;

R = 284;

SCp = 9744,099609;

R2 = 10124;

Cpi = 358409,6875;

det В = 336;

det В1 = ─ 3139086,75;

det В2 = 99953,210937;

B 0 = ─ 9342,52058;

B 1 = 297,479797;

Аппроксимирующая функция

P = ─ 9342,52058 + 297,479797* T /

Данная аналитическая зависимость, неудовлетворительно обобщает экспериментальные данные табл.01.

Аномалии и допустимые значения исходных данных.

В результате тестирования программы выявлены следующие её особенности:

1. Допустимые значения исходных данных лежат в пределах [-10000000; +10000000 ];

2. При больших значениях аргумента вычерчивание графика замедляется;

3. При значениях исходных данных в пределах 10^-9 - график функции может быть не виден вследствие слишком мелкого масштаба.

Результаты выполнения задания

1. После ввода выходных данных, перед проведением вычислений для выбора вида аппроксимирующей функции представим экспериментальные данные в графическом виде (СНИМОК I ).

2. При вычислении аппроксимирующей функции 2 –й степени программа вывела на экран (СНИМОК II ) :

- вид аппроксимирующего полинома: P = 25440,380859 ─ 1670,317871* T + 27,71546* T ² ;

- dP иdP (%) – ошибки аппроксимации .Сравнительный анализ погрешностей показывает, что полученная аналитическая зависимость удовлетворительно обобщает исходные экспериментальные данные. Максимальная ошибка аппроксимации σP_max = 10,539856(2,9253%), минимальная - σP_min = 4,473511 (0,365573%);

- ITG - интегральную оценку аппроксимации. Для интегральной оценки аппроксимации использована формула:

ITG =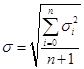=8,179605;

После завершения вычислений построим график аппроксимирующей функции и сравним его с графиком, построенным по выходным данным таблицы 01. Сравнивая графики можно определить хорошую сходимость теоретических и экспериментальных

3. При вычислении аппроксимирующей функции 1 – й степени программа вывела на экран

- вид аппроксимирующего полинома:

P = ─ 9342,520508 + 297,479797* T ;

- dCP иdCP (%) –абсолютную и относительную ошибки аппроксимации. Сравнительный анализ погрешностей показывает, что полученная аналитическая зависимость неудовлетворительно обобщает исходные экспериментальные данные.

Максимальная абсолютная ошибка аппроксимации

dCP - σP_max = 204,608398(8,3045868%),

минимальная абсолютная ошибка аппроксимации

dCP - σP_min = 20,088257(1,013637%).

Максимальная относительная ошибка аппроксимации

dCp (%) - σP_max = 50,920618% (183,46698),

минимальная относительная ошибка аппроксимации

dCp (%) - σP_min = 1,013637%(20,088257).

- ITGL - интегральную оценку аппроксимации.

ITGL = 120,015892;

После завершения вычислений построим график аппроксимирующей функции и сравним его с графиком, построенным по выходным данным таблицы 01. Сравнивая графики, а также значения

dCP ,dCP (%) и ITGL можно определить неудовлетворительную сходимость теоретических и экспериментальных данных.

4. После запуска программы на экране появляется приглашение < Enter input dates > , предлагающее пользователю ввести количество пар входных данных, после чего выводится строка ввода значений аргумента < ENTER EXPERIMENTAL ARGUMENT VALUE > и затем значений экспериментальной зависимости <ENTER EXPERIMENTAL DEPENDENCY VALUE> .

После ввода данных на экран выводится меню:

FOR DRAWING POINTS INPUT <1>;

FOR FIND APROCSIMATION POLINOM FUNCTION INPUT <2>;

FOR DRAWING THE GRAPHIC OF POLINOM FUNCTION INPUT <3>;

FOR FIND APROCSIMATION LINEAR FUNCTION INPUT <4>;

FOR DRAWING THE GRAPHIC OF LINEAR FUNCTION INPUT<5>;

FOR EXIST INPUT <0>,

состоящее из 6 пунктов, выбрав один из которых можно произвести соответствующие операции, указанные в аннотации:

- FOR DRAWING POINTS INPUT <1> - позволяет произвести графическое отображение экспериментальных данных в виде точек зависимости P = f(t) на координатной плоскости ;

FOR FIND APROCSIMATION POLINOM FUNCTION INPUT <2> - позволяет произвести расчет функции аппроксимации экспериментальных данных в виде полинома 2 - й степени;

FOR DRAWING THE GRAPHIC OF POLINOM FUNCTION INPUT <3> - позволяет построить графическое отображение, полученной зависимости P = f ( t ) в виде аппроксимирующего многочлена 2 степени, на координатной плоскости;

FOR FIND APROCSIMATION LINEAR FUNCTION INPUT <4> - позволяет произвести расчет линейной функции аппроксимации экспериментальных данных;

FOR DRAWING THE GRAPHIC OF LINEAR FUNCTION INPUT <5> - позволяет построить графическое отображение, полученной зависимости P = f ( t ) в виде линейной функции аппроксимации на, координатной плоскости;

FOR EXIST INPUT <0> - предлагает выйти из программы:

Вывод

Данная программа позволяет произвести аппроксимацию экспериментальных зависимостей методом наименьших квадратов с отображением результатов аппроксимации в текстовом и графическом режимах. Программа позволяет оценить точность аппроксимации и произвести сравнительный анализ типов аппроксимации ( с помощью многочлена 2 – й степени или с помощью многочлена 1 – й степени ).

Список литературы

Яремчук Ф.П., Рудченко П.А. АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ - Киев, НАУКОВА ДУМКА, 1987, 647.

Глушаков С.В., Сурядный А.С. MICROSOFT EXCEL XP - Харьков, ФИЛИО, 2006, 508.

Дорош Н.Л., Бартенев Г.Л. и др. Методические указания к выполнению индивидуальных заданий и курсовой работы по дисциплинам "Информатика" и "Вычислительная математика". Днепропетровск, УДХТУ, 2004, 47.