Название: Линеаризация без метода наименьших квадратов
Вид работы: доклад
Рубрика: Математика
Размер файла: 22.3 Kb
Скачать файл: referat.me-214842.docx
Краткое описание работы: Метод наименьших квадратов настолько прочно вошел в жизнь экспериментатора, что альтернативные методы линеаризации почти не рассматриваются.
Линеаризация без метода наименьших квадратов
Метод наименьших квадратов настолько прочно вошел в жизнь экспериментатора, что альтернативные методы линеаризации почти не рассматриваются. Безусловно, если существует задача нахождения одной результирующей прямой, то искать замену традиционному методу наименьших квадратов не рационально. Решение более сложной задачи требует дополнительных шагов по усовершенствованию процесса расчетов. Приведем пример. Известно, что массив экспериментальных результатов может не принадлежать одной прямой. Более того, разные области массива могут принадлежать разным прямым. В этом случае применять метод наименьших квадратов в традиционном виде нельзя, так как его надо сочетать с процедурой исключения точек, не принадлежащих искомой прямой, что существенно усложняет расчеты.
Цель может быть достигнута более простым методом! Рассмотрим один из таких простых методов.
В основе метода лежит далеко не свежая идея о вычислении параметров прямой между всеми возможными парами экспериментальных точек. (Следует обратить внимание на то, что параметры вычисляются не только между соседними точками!) Выбирается, например, какая-либо точка, и вычисляются параметры прямых, которые можно провести между этой точкой и всеми остальными. Затем выбирается следующая точка и с ней проделывается та же операция. В итоге получается массив данных о параметрах прямых размером в n(n-1)/2 элементов, где n - число обрабатываемых экспериментальных точек. Если читатель думает, что автор статьи сейчас предложит просто усреднить полученные результаты, найдя их среднее арифметическое, то он глубоко ошибается! Вычисление среднего арифметического ничего нового не вносит в математическую обработку, так как предполагает, что все экспериментальные точки лежат на одной прямой. Прежде чем продолжить изложение материала, договоримся о том, что массивы найденных параметров прямых A и B следует преобразовать в один. Вновь образованный массив организуется умножением одного параметра прямой на другой, т.е. A*B. Необходимость этого шага будет ясна в дальнейшем.
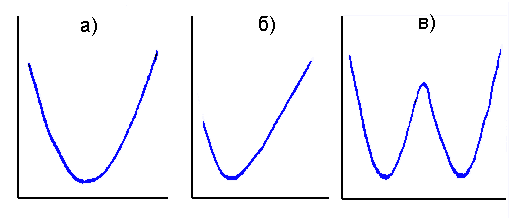
Над новым массивом проведем 2 следующие операции. Во-первых, проведем сортировку массива по возрастанию значений элементов массива. Во-вторых, после сортировки вычислим разности между каждыми 2-мя соседними элементами массива. После этого следует рассмотреть функцию изменения разностей от абсолютного значения A*B. График этой функции F(A*B) будет иметь один или несколько ярко выраженных минимумов. Число этих экстремумов будет соответствовать числу прямых, которые можно провести через экспериментальные точки. Например, рис. а) свидетельствует о том, что массив данных допускает линеаризацию одной прямой. Среднее положение минимума функции F(A*B) относительно интервала рассматриваемых значений A*B свидетельствует о том, что систематических отклонений от прямой линии практически не существует. Рисунок б) говорит о том, что часть точек имеет систематическое отклонение от линейной закономерности, так как минимум функции смещен от середины отрезка значений A*B. На рисунке в) рассмотрен случай, когда экспериментальные данные линеаризуются 2-мя прямым.
 |
После того, как анализ функции проведен, наступает следующий важный этап расчетов - определение параметров линеаризующих прямых. Есть 2 способа. Первый способ состоит в том, что во время проведения сортировки и вычисления разностей запоминаются значения A и B. Из этого следует, что каждому значению вычисленных разностей соответствуют значения A и B. Тогда, зная значение A*B в минимуме нашей функции (см. рис. а)), можно найти значения A и B. Однако в выборе точек минимума следует быть осторожным, так как наименьшее значение A*B может быть случайным совпадением. Для того чтобы этого избежать, надо усреднить несколько значений в окрестности минимума. Развивая тему о случайности некоторых значений функции F(A*B), надо отдавать себе отчет в том, что на фоне минимума организованного большими группами точек, неизбежны экстремумы из малых групп, которые образованы случайными совпадениями. Для того чтобы их было меньше, автор и предложил ранее анализ массива из значений A*B, так как операции только со значениями A и B приводят к существенному увеличению числа случайных экстремумов.
Второй способ похож на первый, но вместо запоминания всех параметров A и B, запоминаются только порядковые номера точек. Таким образом, после выделения окрестности функции F(A*B), производится выделение групп "благонадежных" точек. Их линеаризация позволяет найти искомые значения A и B. Второй способ более выгоден для целей создания компьютерных программ, так как оперативная память экономится эффективнее.
Подведем итоги.
Во-первых, новый метод позволяет не только вычислять параметры прямой, но и анализировать экспериментальные результаты на принадлежность нескольким прямым, что для экспериментатора тоже важно. Во-вторых, возможна обработка результатов, которые не могут быть линеаризованы из-за трансцендентного характера аппроксимирующей функции, например, Y=B*lg(1+A*X). В этом случае гораздо легче вычислять параметры по 2-м точкам, чем заниматься выводом индивидуальных формул методом наименьших квадратов, вычисление по которым нужно проводить только методами вычислительной математики.
Похожие работы
-
Анализ наименьших квадратов и полиномы второго порядка
Подход с использованием наименьших квадратов выстраивает прямую линию через ряд цен в течение прошлого периода времени так, чтобы различие между каждой отдельной ценой и прямой линией было наименьшим.
-
Алгебраическое доказательство теоремы Пифагора
Доказательство теоремы Пифагора методами элементарной алгебры: методом решения параметрических уравнений в сочетании с методом замены переменных. Существование бесконечного количества троек пифагоровых чисел и, соответственно, прямоугольных треугольников.
-
Аппроксимация функций
Способы задания функциональных зависимостей: аналитический, графический, табличный; аппроксимирующая функция.
-
Математика
Министерство науки, высшей школы и технической политики Российской Федерации. Новосибирский Государственный Технический Университет. Контрольная работа по специальным главам математики.
-
Эконометрика
Обработка результатов наблюдений за дневной выручкой восьми продавцов на рынке.
-
Прогнозирование функций по методу наименьших квадратов
Министерство общего и профессионального образования Московский Авиационный институт (государственный технический университет) «МАИ» ОТЧЕТ О НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЕ
-
Интерполирование и приближение функций
Разделенные разности и аппроксимация функций методом наименьших квадратов. Интерполяционные многочлены Лагранжа и Ньютона. Экспериментальные данные функциональной зависимости. Система уравнений для полинома. Графики аппроксимирующих многочленов.
-
Интегралы, объем тела вращения, метод наименьших квадратов
Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.
-
Метод наименьших квадратов в случае интегральной и дискретной нормы Гаусса
1. Постановка задачи При решении многих задач физики и других прикладных наук возникает необходимость вместо функции , рассматривать функцию , представляющую функцию
-
Множественная регрессия и корреляция 2
Множественная регрессия и корреляция Пусть требуется построить линейную модель зависимости некоторого выходного экономического показателя , называемого объясняемой переменной от набора входных показателей