Название: Задача по Экономико-математическое моделирование

Вид работы: реферат

Рубрика: Математика

Размер файла: 29.6 Kb

Скачать файл: referat.me-217965.docx

Краткое описание работы: ФЕДЕРАЛЬНОЕ Вариант № . Нефтеперерабатывающий завод производит в месяц 1500000 л алкилата, 1200000 л крекинг - бензина и 1300000 л изопентола. В результате смешения этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 и 120 усл. ед..

Задача по Экономико-математическое моделирование

ФЕДЕРАЛЬНОЕ Вариант № .

Нефтеперерабатывающий завод производит в месяц 1500000 л алкилата, 1200000 л крекинг - бензина и 1300000 л изопентола. В результате смешения этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 и 120 усл. ед.. Определить месячный план производства бензина сорта А и Б, приносящий предприятию максимальную прибыль.

Решите задачу графическим и симплекс-методом. Выполните постановку и найдите решение двойственной задачи.

1. Графический метод решения

Характеристика	Бензин		Ограничения
	А	Б
Алкилат	1	3	1500
Крекинг – бензина	1	1	1200
Изопентол	1	2	1300
Прибыль (за 1000л)	90	120
План	х1	х2

х₁ + 3х₂ < 1500,

х₁ + х₂ < 1200,

х₁ + 2х₂ < 1300,

х₁ > 0, х₂ > 0.

Целевая функция:

f = 90х₁ + 120х₂ → max.

Строим прямые

х₁ + 3х₂ = 1500, 1

х₁ + х₂ = 1200, 2

х₁ +2 х₂ = 1300. 3

Строим направляющий вектор q {90, 120}.

Строим прямую, перпендикулярную направляющему вектору и проходящую через область допустимых решений.

Находим оптимальный план:

х₁ + х₂ = 1200, х₁ = 1100,

х₁ +2 х₂ = 1300. х₂ = 100.

Максимальная прибыль допускается при выпуске 1100 бензина А и 100 бензина Б.

Оптимальное значение целевой функции:

f = 90х₁ + 120х₂ , f = 90∙1100 + 120∙100 = 111000.

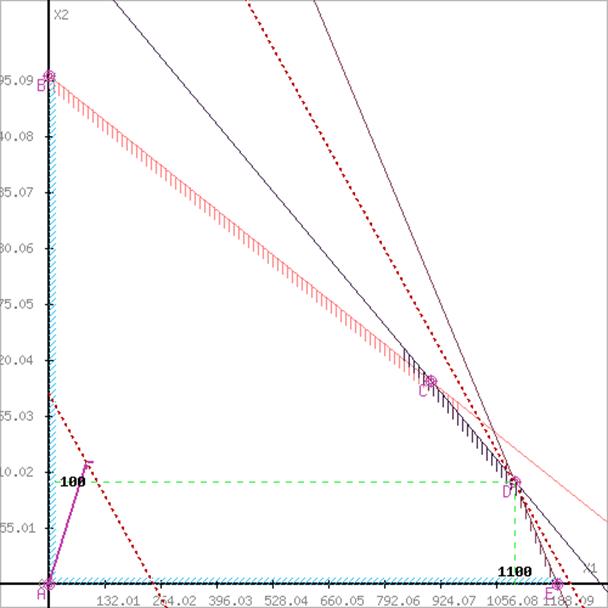2. Симплекс-метод.

Характеристика	Бензин		Ограничения
	А	Б
Алкилат	1	3	1500
Крекинг – бензина	1	1	1200
Изопентол	1	2	1300
Прибыль (за 1000л)	90	120
План	х1	х2

Ограничения:

х₁ + 3х₂ < 1500,

х₁ + х₂ < 1200,

х₁ + 2х₂ < 1300,

х₁ > 0, х₂ > 0.

Целевая функция: f = 90х₁ + 120х₂ → max,

Введем дополнительные переменные у₁ , у₂ , у₃ .

1х₁ + 3х₂ + у₁ = 1500,

1х₁ + 1х₂ + у₂ = 1200,

1х₁ + 2х₂ + у₃ = 1300,

х₁ > 0, х₂ > 0,

у₁ > 0, у₂ > 0, у₃ > 0.

у₁ = 1500 – (1х₁ + 3х₂ ),

у₂ = 1200 – (1х₁ + 1х₂ ),

у₃ = 1300 – (1х₁ + 2х₂ ),

х₁ > 0, х₂ > 0,

у₁ > 0, у₂ > 0, у₃ > 0.

f = 0 – (-90х₁ – 120х₂ ) → max.

Составим симплекс таблицу:

Базисные переменные	Свободные члены	x1	x2
у1	1500	1	3
у2	1200	1	1
у3	1300	1	2
Индексная строка	0	-90	-120

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в индексной строке есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в индексной строке (-120). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.

Пересчитаем таблицу

Базисные переменные	Свободные члены	x1	у1
x2	500	1/3	1/3
у2	700	2/3	-1/3
у3	300	1 / 3	-2/3
Индексная строка	60000	-50	40

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в индексной строке есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в индексной строке (-50). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.

Пересчитаем таблицу

Базисные переменные	Свободные члены	у3	у1
X2	200	-1	1
у2	100	-2	1
X1	900	3	-2
Индексная строка	105000	150	-60

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в индексной строке есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в индексной строке (-60). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.

Пересчитаем таблицу

Базисные переменные	Свободные члены	у3	у2
x2	100	1	-1
у1	100	-2	1
x1	1100	-1	2
Индексная строка	111000	30	60

Найдено оптимальное решение.

3. Постановка и решение двойственной задачи.

Основная задача:

х₁ + 3х₂ < 1500,

х₁ + х₂ < 1200,

х₁ + 2х₂ < 1300,

х₁ > 0, х₂ > 0.

Целевая функция:

f = 90х₁ + 120х₂ → max.

Целевая функция двойственной задачи:

g = 1500y₁ + 1200y₂ + 1300y₃ → min.

у₁

1 1 1 ∙ у₂

3 1 2 у₃

1у₁ + 1у₂ + 1у₃ > 90,

3у₁ + 1у₂ + 2у₃ > 120.

Переход от неравенства к равенству:

х₁ + 3х₂ + х₃ = 1500,

х₁ + х₂ + х₄ = 1200,

х₁ + 2х₂ + х₅ = 1300,

х_i > 0.

1у₁ + 1у₂ + 1у₃ - у₄ = 90,

3у₁ + 1у₂ + 2у₃ - у₅ = 120.

у_i > 0.

Осн.	Осн.		Доп.
	х1	х2	х3	х4	х5
	1100	100	100	0	0
Двойст.	0	0	0	60	30
	у4	у5	у1	у2	у3
	Доп.		Осн.