Название: Сетка Вульфа

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 346.67 Kb

Скачать файл: referat.me-218233.docx

Краткое описание работы: Сетка Вульфа или стереографическая сетка представляет собой проекцию меридианов и параллелей сферической поверхности на плоскость одного из меридианов, называемого в этом случае ОСНОВНЫМ. Центром проекции является точка ЭКВАТОРА сферы, удаленная от основного меридиана на (

Сетка Вульфа

Сетка Вульфа или стереографическая сетка представляет собой проекцию меридианов и параллелей сферической поверхности на плоскость одного из меридианов, называемого в этом случае ОСНОВНЫМ. Центром проекции является точка ЭКВАТОРА сферы, удаленная от основного меридиана на (), например, если мы используем градусную систему счисления, то это будет .

Стереографическая проекция обладает тем важным свойством, что дуга любого круга на сфере изображается в этой проекции так же дугой круга.

Для определенности на сетке вводятся следующие названия

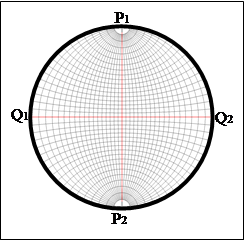
· Окружность сетки называют ее ОСНОВНЫМ МЕРИДИАНОМ. Напомню, что это может быть ЛЮБОЙ из возможных меридианов.

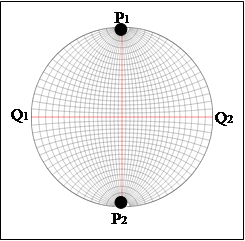
· Точки, в которых сходятся ВСЕ меридианы, называются ПОЛЮСАМИ СЕТКИ.

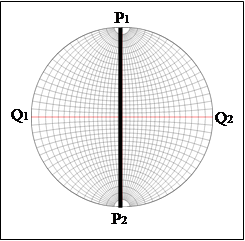
· Диаметр , проходящий через полюса сетки, называется ОСЬЮ СЕТКИ.

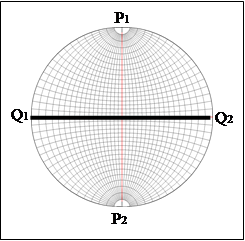
· Диаметр , перпендикулярный к оси сетки, называется ЭКВАТОРОМ СЕТКИ.

Методика построения сетки Вульфа

Построение линий меридианов

Исходные данные

В исходной окружности, радиус которой равен , линия меридиана, долгота которого равна , представляет собой дугу окружности, которая проходит через следующие точки:

· Точку B;

· Точку A;

· Точку C.

Точки В и С являются точками пересечения диаметра окружности с линией окружности. Точка А лежит на прямой, проходящей через центр окружности , и перпендикулярной диаметру ВС.

Положение точки А на прямой определяется, как точка пересечения этой прямой с одной из сторон вписанного угла,

· вершиной которого является точка В,

· одной из сторон которого является диаметр окружности - ВС

· другой стороной угла является луч, проходящий через точку D, лежащую на окружности и отстоящей от точки С на расстоянии, равном долготе меридиана . Это расстояние определяется длиной дуги

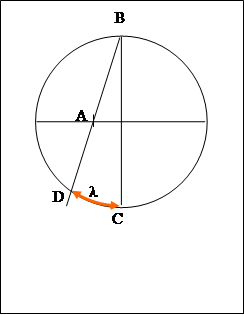
Таким образом, нам надо по положению трех точек (А, В. С) определить радиус некоторой окружности , так чтобы эти точки (А, В, С) лежали на окружности .

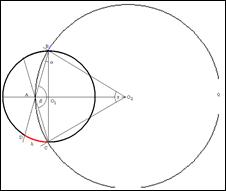
Решение.

Угол обозначим как

Угол обозначим как

Угол обозначим как

1. , как вписанный угол, опирающийся на дугу, длина которой равна

2. Треугольник - равнобедренный, так как точка А лежит на линии, которая

· Проходит через центр окружности

· Перпендикулярна диаметру

3. Отсюда: угол

Рассмотрим окружность и найдем длину дуги этой окружности

4. Угол является вписанным углом окружности . Значит, дуга окружности, на которую опирается этот угол, будет в два раза больше, чем сам угол.

5. Дуга является дополнением дуги до полной окружности. Таким образом, длина дуги определится как:

6. Угол является центральным углом окружности . Он опирается на дугу , следовательно:

Вычислим радиус окружности

7. Рассмотрим треугольник :

· Этот треугольник – прямоугольный.

· Катет равен радиусу исходной окружности , то есть

· Катет лежит против угла, равного

8. Отсюда получаем: 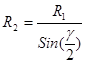Но, учитывая, что , окончательно имеем:

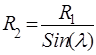
Построение линий параллелей

Исходные данные

В исходной окружности, радиус которой равен , линия параллели, широта которой равна , представляет собой дугу окружности, которая проходит через следующие точки:

· Точку B;

· Точку A;

· Точку C.

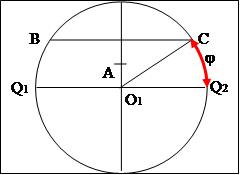
Точки В и С являются точками хорды , которая параллельна диаметру окружности , называемому ЭКВАТОРОМ. Хорда отстоит от экватора на расстоянии, определенном широтой параллели (угол ). Точка А лежит на прямой, проходящей через центр окружности , и перпендикулярной экватору.

Положение точки А на прямой определяется, как точка пересечения этой прямой с одной из сторон вписанного угла,

· вершиной которого является точка В,

· одной из сторон которого является хорда окружности - ВС

· другой стороной угла является луч, проходящий через точку пересечения экватора окружности с линией окружности (точка )

Таким образом, нам надо по положению трех точек (А, В. С) надо определить радиус некоторой окружности , так чтобы эти точки (А, В, С) лежали на окружности .

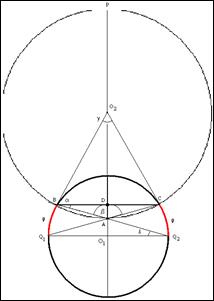
Решение.

Угол обозначим как

Угол обозначим как

Угол обозначим как

Угол обозначим как

1. Определим величину угла .

Рассмотрим угол . Он является вписанным углом окружности и опирается на дугу, длина которой равна . Следовательно, величина угла равна половине дуги, на которую он опирается.

Очевидно, что угол , как накрест лежащие углы. Значит

2. Определим величину угла .

Треугольник - равнобедренный, так как точка А лежит на линии, которая

· Проходит через центр окружности

· Перпендикулярна хорде, которая параллельна экватору окружности

Отсюда: угол

Рассмотрим окружность и найдем длину дуги этой окружности

3. Угол является вписанным углом окружности . Значит, дуга окружности, на которую опирается этот угол, будет в два раза больше, чем сам угол.

4. Дуга является дополнением дуги до полной окружности. Таким образом, длина дуги определится как:

5. Угол является центральным углом окружности . Он опирается на дугу , следовательно:

Вычислим радиус окружности

6. Рассмотрим треугольник :

· Этот треугольник – прямоугольный.

· Катет равен половине хорды , длину которой обозначим как

· Катет лежит против угла, равного

7. Отсюда получаем: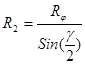

Но, учитывая, что , имеем: , где . Подставив вместо его выражение, окончательно получим:

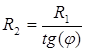
Как начертить линию меридиана, долгота которого 

Решить эту задачу можно чисто графически, используя только циркуль и линейку. Но это “высший пилотаж”. Если Вы захотите попробовать, – пожелаю Вам успеха. Сейчас же мы воспользуемся теми выводами, которые получили ранее. Итак, начинаем. Нам потребуется БОЛЬШОЙ лист бумаги, карандаш, линейка, циркуль и калькулятор, которые может быть заменен тригонометрическими таблицами.

1. Задаем размер стереографической сетки, тем самым мы определяем величину радиуса стереографической сетки (или окружности )

2. По выведенной ранее формуле, вычисляем величину радиус окружности , дуга которой и будет отображать желаемую линию меридиана.

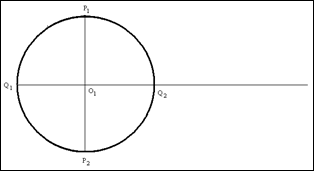
3. На листе бумаги обозначаем центр окружности стереографической проекции и чертим окружность, радиус которой равен , при этом мы не забываем провести в этой окружности линии ЭКВАТОРА СЕТКИ и ОСИ СЕТКИ.

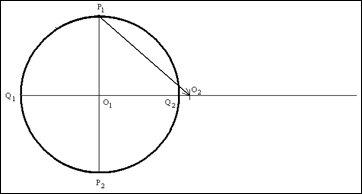
4. Из одного из полюсов стереографической сетки при помощи циркуля, раствор которого равен величине радиуса , на продолжении линии экватора , делаем засеку. Это будет центром окружности, дуга которой и будет отображать линию искомого меридиана. Обозначим эту точку, как

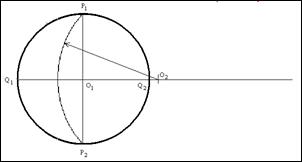
5. Не меняя раствора циркуля, из точки , как центра окружности, чертим дугу окружности . Эта дуга будет изображать линию искомого меридиана.

Чтобы построить симметричную линию меридиана, долгота которого будет равна (), поступим аналогично тому, как мы поступали при построении линии меридиана, долгота которого равна .

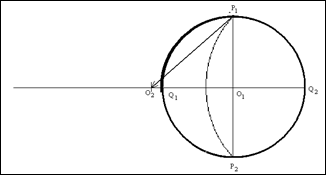
6. Из одного из полюсов стереографической сетки при помощи циркуля, раствор которого равен величине радиуса , на продолжении линии экватора , делаем засеку. Это будет центром окружности, дуга которой и будет отображать линию искомого меридиана. Обозначим эту точку, как

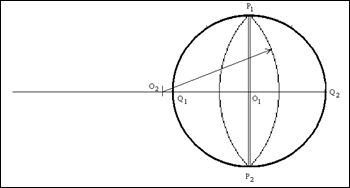
7. Не меняя раствора циркуля, из точки , как центра окружности, чертим дугу окружности . Эта дуга будет изображать линию искомого меридиана.

Как начертить линию параллели, широта которой 

Решить эту задачу можно чисто графически, используя только циркуль и линейку. Но это “высший пилотаж”. Если Вы захотите попробовать, – пожелаю Вам успеха.

Сейчас же мы воспользуемся теми выводами, которые получили ранее. Итак, начинаем. Нам потребуется БОЛЬШОЙ лист бумаги, карандаш, линейка, циркуль и калькулятор, которые может быть заменен тригонометрическими таблицами.

1. Задаем размер стереографической сетки, тем самым мы определяем величину радиуса стереографической сетки (или окружности )

2. По выведенной ранее формуле, вычисляем величину радиус окружности , дуга которой и будет отображать желаемую линию параллели.

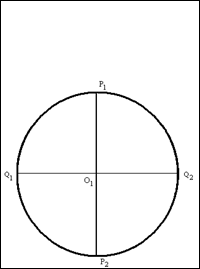
3. На листе бумаги обозначаем центр окружности стереографической проекции и чертим окружность, радиус которой равен , при этом мы не забываем провести в этой окружности линии ЭКВАТОРА СЕТКИ и ОСИ СЕТКИ.

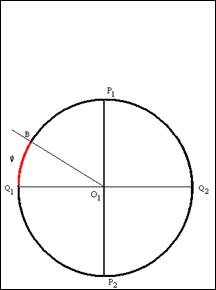
4. Из центра окружности под углом к линии экватора проводим луч. Точку пересечения луча с линией окружности обозначим как точку

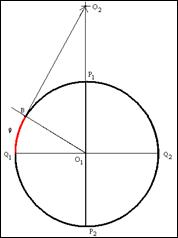
5. Из точки при помощи циркуля, раствор которого равен величине радиуса , на продолжении линии оси сетки , делаем засеку. Это будет центром окружности, дуга которой и будет отображать линию искомой параллели. Обозначим эту точку, как

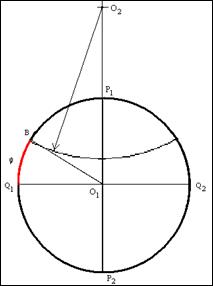
6. Не меняя раствора циркуля, из точки , как центра окружности, чертим дугу окружности. Эта дуга будет изображать линию искомой параллели

Чтобы построить симметричную линию параллели, широта которой будет равна (), поступим аналогично тому, как мы поступали при построении линии параллели, широта которой равна .

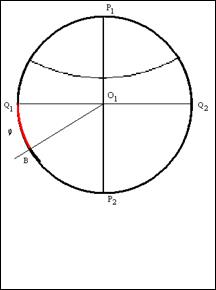
7. Из центра окружности под углом () к линии экватора проводим луч. Точку пересечения луча с линией окружности обозначим как точку

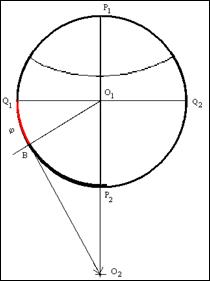
8. Из точки при помощи циркуля, раствор которого равен величине радиуса , на продолжении линии оси сетки , делаем засеку. Это будет центром окружности, дуга которой и будет отображать линию искомой параллели. Обозначим эту точку, как

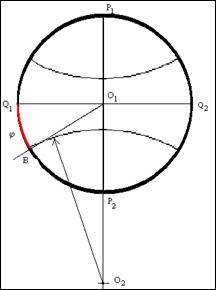
9. Не меняя раствора циркуля, из точки , как центра окружности, чертим дугу окружности. Эта дуга будет изображать линию искомой параллели