Название: Правильные многогранники

Вид работы: реферат

Рубрика: Математика

Размер файла: 144.78 Kb

Скачать файл: referat.me-218268.docx

Краткое описание работы: Определение правильного многогранника. Определение. Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани – равные друг другу правильные многоугольники; 3) в каждой его вершине сходится одинаковое число ребер; 4) все его двугранные равны.

Правильные многогранники

Определение правильного многогранника.

Определение. Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани – равные друг другу правильные многоугольники; 3) в каждой его вершине сходится одинаковое число ребер; 4) все его двугранные равны.

Примером правильного многогранника является куб: он является выпуклым многогранником, все его грани – равные квадраты, в каждой вершине сходятся три ребра, и все двугранные углы куба прямые. Правильный тетраэдр также является правильным многогранником.

Возникает вопрос: сколько существует различных типов правильных многогранников?

Пять типов правильных многогранников.

Рассмотрим произвольный правильный многогранник М , у которого В вершин, Р ребер и Г граней. По теореме Эйлера для этого многогранника выполняется равенство:

В - Р + Г = 2. (1)

Пусть каждая грань данного многогранника содержит m ребер (сторон), и в каждой вершине сходятся n ребер. Очевидно,

m, n. (2)

Так как у многогранника В вершин, и каждой из которых сходятся n ребер, то получаем nребер. Но любое ребро соединяет две вершины многогранника, поэтому в произведение n каждое ребро войдет дважды. Значит у многогранника имеется различных ребер. Тогда

= Р В = . (3)

Далее, в каждой грани многогранника М содержится m ребер, а число граней равно Г. Так как каждое ребро принадлежит двум смежным граням, то число различных ребер многогранника равно . Тогда

=Р Г=. (4)

Из (1), (3), (4) получаем - Р + = 2, откуда

+ = + > . (5)

Таким образом, имеем

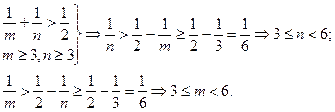
Из неравенств 3 и 3 следует, что гранями правильного многогранника могут быть либо правильные треугольники, либо правильные четырехугольники, либо правильные пятиугольники. Причем в случаях m = n = 4; m= 4, n = 5; m = 5, n = 4; m = n = 5 приходим к противоречию с условием . Поэтому остаются возможными пять случаев: 1) m = n = 3; 2) m = 4, n = 3; 3) m = 3, n = 4; 4) m = 5, n = 3; 5) m = 3, n = 5.

Рассмотрим каждый из этих случаев, используя соотношения (5), (4) и (3).

1) m = n = 3 (каждая грань многогранника – правильный треугольник. Это – известный нам правильный тетраэдр («тетраэдр » означает четырехгранник).

2) m = 4, n = 3 (каждая грань квадрат, и в каждой вершине сходятся три ребра). Имеем

Р = 12; В = 8; Г = 6.

Получаем правильный шестигранник, у которого каждая грань – квадрат. Этот многогранник называется правильным гексаэдром и является кубом («гексаэдр» -- шестигранник), любой параллелепипед – гексаэдр.

3) m = 3, n = 4 (каждая грань –правильный треугольник, в каждой вершине сходятся четыре ребра). Имеем

Р = 12; В = =6; Г = =8.

Получаем правильный восьмигранник, у которого каждая грань – правильный треугольник. Этот многогранник называется правильным октаэдром («октаэдр» -- восьмигранник).

4) m= 5, n= 3 (каждая грань – правильный пятиугольник, в каждой вершине сходятся три ребра). Имеем:

Р = 30; В = = 20; Г = = 12.

Получаем правильный двенадцатигранник, у которого каждая грань – правильный пятиугольник. Этот многогранник называется правильным додекаэдром («додекаэдр » -- двенадцатигранник).

5) m = 3, n = 5 (каждая грань – правильный треугольник, в каждой вершине сходятся пять ребер). Имеем

Р = 30; В = =12; Г = = 20.

Получаем правильный двадцатигранник. Этот многогранник называется правильным икосаэдром («икосаэдр » - двадцатигранник).

Таким образом, мы получили следующую теорему.

Теорема. Существует пять различных ( с точностью до подобия) типов

правильных многогранников: правильный тетраэдр, правильный гексаэдр

(куб), правильный октаэдр, правильный додекаэдр и правильный икосаэдр.

К этому заключению можно прийти несколько иначе.

Действительно, если грань правильного многогранника – правильный треугольник, и в одной вершине сходятся k ребер, т.е. все плоский углы выпуклого k -гранного угла равны , то . Следовательно, натуральное число k может принимать значения: 3;4;5. при этом Г = , Р = . На основании теоремы Эйлера имеем: В+-= 2 или В ( 6 – k ) = 12. Тогда

при k = 3 получаем: В = 4, Г = 4 , Р = 6 (правильный тетраэдр);

при k = 4 получаем: В = 6, Г = 8, Р = 12 (правильный октаэдр);

при k = 5 получаем: В = 12, Г = 20, Р = 30 (правильный икосаэдр).

Если грань правильного многогранника – правильный четырехугольник , то . Этому условию соответствует единственное натуральное число k = 3. Тогда: Г = , Р= ; В + - = 2 или . Значит, В = 8, Г = 6, Р = 12 – мы получаем куб (правильный гексаэдр).

Если гранью правильного многогранника является правильный пятиугольник, то . Этому условию соответствует тоже только k = 3 и Г = ; Р = . Аналогично предыдущим вычислениям получаем: и В = 20, Г = 12, Р = 30 (правильный додекаэдр).

Начиная с правильных шестиугольников, предположительно являющихся гранями правильного многогранника, плоские углы становятся не меньше , и уже k = 3 их сумма становится не менее , что невозможно. Следовательно, существует всего пять видов правильных многогранников.

На рисунках изображены разверстки каждого из пяти правильных многогранников.

Правильный тетраэдр

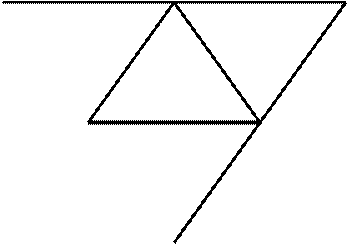
Правильный октаэдр

Правильный гексаэдр

Правильный икосаэдр

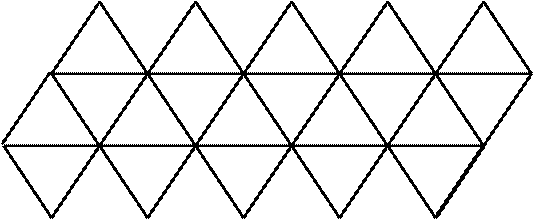
Правильный додекаэдр

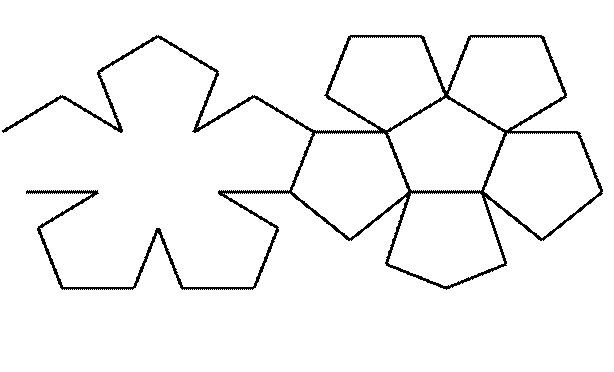
Некоторые свойства правильных многогранников приведены в следующей таблице.

Вид грани	Плоский угол при вершине	Вид многогранного угла при вершине	Сумма плоских углов при вершине	В	Р	Г	Название многогранника
Правильный треугольник		3-гранный		4	6	4	Правильный тетраэдр
Правильный треугольник		4-гранный		6	12	8	Правильный октаэдр
Правильный треугольник		5-гранный		12	30	20	Правильный икосаэдр
Квадрат		3-гранный		8	12	6	Правильный гексаэдр (куб)
Правильный пятиугольник		3-гранный	ё	20	30	12	Правильный додекаэдр

У каждого из правильных многогранников, помимо уже указанных, нас чаще всего будут интересовать:

1. Величина его двугранного угла при ребре (при длине ребра a ).

2. Площадь его полной поверхности (при длине ребра a ).

3. Его объем (при длине ребра a ).

4. Радиус описанной около него сферы (при длине ребра a ).

5. Радиус вписанной в него сферы (при длине ребра a ).

6. Радиус сферы, касающихся всех его ребер (при длине ребра a ).

Наиболее просто решается вопрос о вычислении площади полной поверхности правильного многогранника; она равна Г, где Г – количество граней правильного многогранника, а - площадь одной грани.

Напомним, sin= , что дает нам возможность записать в радикалах: ctg=. Учитывая это составляем таблицы:

а) для площади грани правильного многогранника

Вид грани	Длина стороны	Длина апофемы грани	Площадь грани
Правильный треугольник	a	0,5
Квадрат	a	0,5a
Правильный пятиугольник	a

б) для площади полной поверхности правильного многогранника

Вид многогранника	Вид граней	Количество граней	Площадь полной поверхности
Правильный тетраэдр	Правильный треугольник	4
Правильный октаэдр	Правильный треугольник	8
Правильный икосаэдр	Правильный треугольник	20
Правильный гексаэдр (куб)	Квадрат	6	6a
Правильный додекаэдр	Правильный пятиугольник	12

Теперь перейдем к вычислению величины двугранного угла правильного многогранника при его ребре. Для правильного тетраэдра и куба вы легко найдете величину этого угла.

В правильном додекаэдре все плоские углы его граней равны , поэтому, применив теорему косинусов для трехгранных углов к любому трехгранному углу данного додекаэдра при его вершине, получим: cos, откуда

.

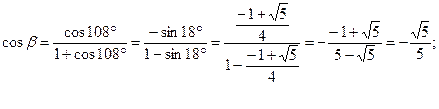
На изображенном правильном октаэдре ABCDMFвы можете убедиться, что двугранный угол при ребре октаэдра равен 2arctg.

C

A

M

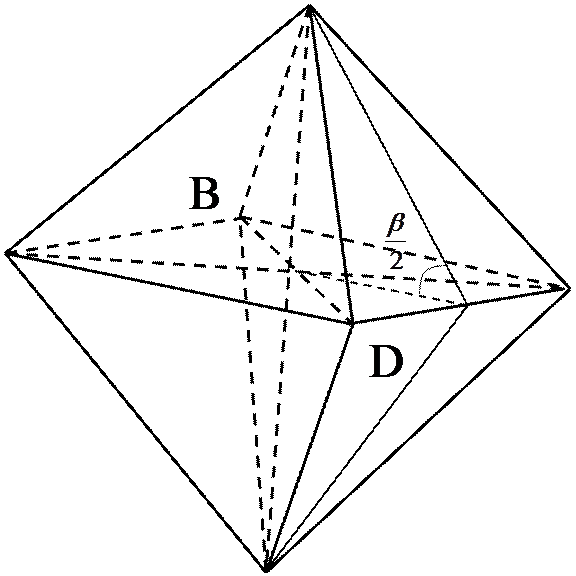
F

Для нахождения величины двугранного угла при ребре правильного икосаэдра можно рассмотреть трехгранный угол ABCD при вершине А: его плоские углы ВАС и CAD равный , а третий плоский угол BAD, против которого лежит двугранный угол B(AC)D = , равен (BCDMF– правильный пятиугольник). По теореме косинусов для трехгранного угла ABCDимеем: . Учитывая, что , получаем , откуда . Таким образом, двугранный угол при ребре икосаэдра равен .

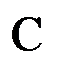
Итак, получаем следующую таблицу величин двугранных углов при ребрах правильных многогранников.

Вид многогранника	Величина двугранного угла при ребре
Правильный тетраэдр
Правильный октаэдр
Правильный гексаэдр (куб)
Правильный додекаэдр
Правильный икосаэдр

Прежде чем находить объем того или иного правильного многогранника, сначала проведем рассуждения о том, как можно найти объем правильных многогранников в общем виде.

Попытайтесь сначала доказать, что если центр каждой грани любого правильного многогранника провести прямую, перпендикулярную плоскости этой грани, то все проведенные прямые пересекутся в некоторой одной точке О , удаленной от всех граней данного многогранника на одно и тоже расстояние, которое обозначим r. Точка О окажется центром сферы, вписанной в данный многогранник, а r – ее радиусом. Соединив полученную точку О со всеми вершинами данного многогранника, мы разобьем его на Г равных между собой пирамид (Г—число граней правильного многогранника): основаниями образованных пирамид равны r . Тогда объем данного многогранника равен сумме объемов всех этих пирамид. Так как многогранник правильный, то его объем V можно найти по формуле:

(1)

Остается найти длину радиуса r . Для этого, соединив точку О с серединой К ребра многогранника, попробуйте убедиться, что наклонная КО к грани многогранника, содержащей ребро, составляет с плоскостью этой грани угол, равный половине величины двугранного угла при этом ребре многогранника; проекция же наклонной КО на плоскость этой грани принадлежит ее апофеме и равна радиусу вписанной в нее окружности. Тогда

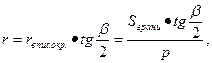
(2)
где p —полупериметр грани. Тогда из (1) и (2) получаем общую для всех правильных многогранников формулу вычисления их объемов:

.

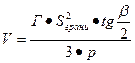Эта формула совершенно не нужна для нахождения объемов куба, правильных тетраэдра и октаэдра, но позволяет довольно легко находить объемы правильных икосаэдра и додекаэдра.

Вид многогранника	Объем многогранника
Правильный тетраэдр
Правильный октаэдр
Куб
Правильный икосаэдр
Правильный додекаэдр

Министерство образования РФ г. Янаул

по геометрии на тему «Правильные многогранники».

Выполнил: Хабибьянов Д.Р.

Проверила: Нургаянова Т.С.

2004 год.