Название: Контрольная работа по Математике
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 135.3 Kb
Скачать файл: referat.me-218299.docx
Краткое описание работы: Контрольная работа №1. Вариант 8. Задание 1. Однажды вечером Ваня и Тима сели играть в кости. Они по очереди бросали две игральные кости. Если сумма выпавших очков равнялась 7, то выигрывал Ваня, а если сумма очков равнялась 8, то выигрывал Тима. На кого бы из них Вы поставили, если бы Вам пришлось держать пари?
Контрольная работа по Математике
Контрольная работа №1.
Вариант 8.
Задание 1.
Однажды вечером Ваня и Тима сели играть в кости. Они по очереди бросали две игральные кости. Если сумма выпавших очков равнялась 7, то выигрывал Ваня, а если сумма очков равнялась 8, то выигрывал Тима. На кого бы из них Вы поставили, если бы Вам пришлось держать пари?
Решение.
Посчитаем число ![]() всевозможных исходов при одном бросании двух игральных костей.
всевозможных исходов при одном бросании двух игральных костей.
При одном бросании двух игральных костей пространство всевозможных исходов ![]() имеет следующий вид
имеет следующий вид ![]() {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33,34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}. Пространство всевозможных исходов
{11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33,34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}. Пространство всевозможных исходов ![]() состоит из 36 элементов. Следовательно,
состоит из 36 элементов. Следовательно, ![]() .
.
![]() {сумма очков равнялась 7}
{сумма очков равнялась 7}
Посчитаем число ![]() исходов, благоприятных событию
исходов, благоприятных событию ![]() .
.
Пространство исходов, благоприятных событию ![]() , имеет следующий вид
, имеет следующий вид ![]() {16, 25, 34, 43, 52, 61}. Пространство исходов, благоприятных событию
{16, 25, 34, 43, 52, 61}. Пространство исходов, благоприятных событию ![]() , состоит из 6 элементов. Следовательно,
, состоит из 6 элементов. Следовательно, ![]() .
.
По классическому определению вероятности ![]() .
.
![]() {сумма очков равнялась 8}
{сумма очков равнялась 8}
Посчитаем число ![]() исходов, благоприятных событию
исходов, благоприятных событию ![]() .
.
Пространство исходов, благоприятных событию ![]() , имеет следующий вид
, имеет следующий вид ![]() {26, 35, 44, 53, 62}. Пространство исходов, благоприятных событию
{26, 35, 44, 53, 62}. Пространство исходов, благоприятных событию ![]() , состоит из 5 элементов. Следовательно,
, состоит из 5 элементов. Следовательно, ![]() .
.
По классическому определению вероятности ![]() .
.
![]() Вероятнее всего, что выиграет Ваня.
Вероятнее всего, что выиграет Ваня.
Ответ. На Ваню.
Задание 2.
Теща Кисы Воробьянинова зашила фамильные бриллианты в один из двенадцати одинаковых стульев. Два из них в последствии остались в Старгороде, а десять стульев отправились в Москву. Какова вероятность отыскать бриллианты в одном из двух стульев, оставшихся в Старгороде?
Решение.
![]() {бриллианты в одном из двух стульев, оставшихся в Старгороде}
{бриллианты в одном из двух стульев, оставшихся в Старгороде}
Посчитаем число ![]() всевозможных исходов. Бриллианты могут находиться в одном из 12 одинаковых стульев. Следовательно,
всевозможных исходов. Бриллианты могут находиться в одном из 12 одинаковых стульев. Следовательно, ![]() .
.
Посчитаем число ![]() исходов, благоприятных событию
исходов, благоприятных событию ![]() . Благоприятным событием является то, что бриллианты находятся в одном из 2 стульев, оставшихся в Старгороде. Следовательно,
. Благоприятным событием является то, что бриллианты находятся в одном из 2 стульев, оставшихся в Старгороде. Следовательно, ![]() .
.
По классическому определению вероятности ![]() .
.
Ответ.
![]()
Задание 3.
Вероятность того, что рабочий перевыполнит план, равна 0.8, а вероятность того, что в случае перевыполнения плана он не получит премию, равна 0.1. Какова вероятность того, что рабочий получит премию?
Решение.
![]() {рабочий перевыполнит план}
{рабочий перевыполнит план}
![]()
![]() {рабочий не перевыполнит план}
{рабочий не перевыполнит план}
![]()
![]() {рабочий получит премию}
{рабочий получит премию}
![]() {рабочий не получит премию}
{рабочий не получит премию}
![]() {рабочий не получит премию при условии, что он перевыполнит план}
{рабочий не получит премию при условии, что он перевыполнит план}
![]()
![]() {рабочий не получит премию при условии, что он не перевыполнит план}
{рабочий не получит премию при условии, что он не перевыполнит план}
![]()
По формуле полной вероятности
![]()
![]()
Ответ.
![]()
Задание 4.
Шахматист завершает вничью в среднем 20% своих партий. Определить наивероятнейшее число ничьих, которые сделает шахматист в турнире, где сыграет 12 партий.
Решение.
![]() количество партий
количество партий
![]() вероятность завершения одной отдельно взятой партии вничью
вероятность завершения одной отдельно взятой партии вничью
![]()
![]() наивероятнейшее число партий, завершенных вничью
наивероятнейшее число партий, завершенных вничью
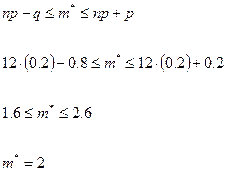
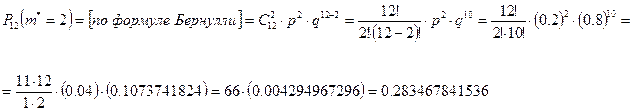
Ответ.
![]()
Задание 5.
Преподаватель проверяет контрольную по теории вероятностей, которую писали студенты трех групп. В первой группе неудовлетворительно написанные контрольные работы составляют 10%, во второй – 15%, в третьей – 20%. Определить вероятность попадания на проверку неудовлетворительно написанной работы, если всего было сдано 18 работ из первой группы, 20 – из второй и 24 из третьей группы.
Решение.
![]() {работа из
{работа из ![]() группы};
группы}; ![]()
![]()
![]()
![]()
![]() {на проверку попала неудовлетворительно написанная работа}
{на проверку попала неудовлетворительно написанная работа}
![]() {на проверку попала неудовлетворительно написанная работа при условии, что она из
{на проверку попала неудовлетворительно написанная работа при условии, что она из ![]() группы};
группы}; ![]()
![]()
![]()
![]()
По формуле полной вероятности
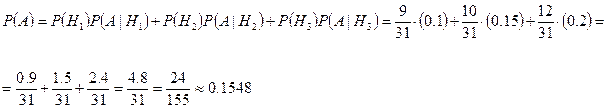
Ответ.
![]()
Контрольная работа №2.
Вариант 8.
Задание 1.
В урне 3 черных и 2 белых шара. Производится последовательное без возвращения извлечение шаров до появления черного. Составить закон распределения случайной величины ![]() числа извлеченных шаров. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
числа извлеченных шаров. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Решение.
Случайная величина ![]() число извлеченных шаров до появления черного шара. Данная случайная величина может принимать следующие значения:
число извлеченных шаров до появления черного шара. Данная случайная величина может принимать следующие значения:
![]() первый извлеченный шар оказался черным
первый извлеченный шар оказался черным
![]() первый извлеченный шар – белый, а второй извлеченный шар оказался черным
первый извлеченный шар – белый, а второй извлеченный шар оказался черным
![]() первые и второй извлеченные шары- белые, а третий извлеченный шар оказался черным
первые и второй извлеченные шары- белые, а третий извлеченный шар оказался черным
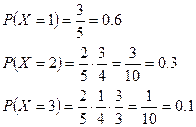
Закон распределения случайной величины ![]() имеет следующий вид:
имеет следующий вид:
![]() математическое ожидание
математическое ожидание
![]()
![]() дисперсия
дисперсия
![]() среднеквадратическое отклонение
среднеквадратическое отклонение
Ответ.
![]()
Задание 2.
Случайная величина ![]() задана функцией распределения
задана функцией распределения ![]() . Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал
. Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал ![]() . Построить графики функций
. Построить графики функций ![]() и
и ![]() .
.
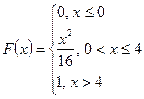
Решение.
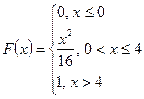
График функции распределения ![]() представлен ниже.
представлен ниже.
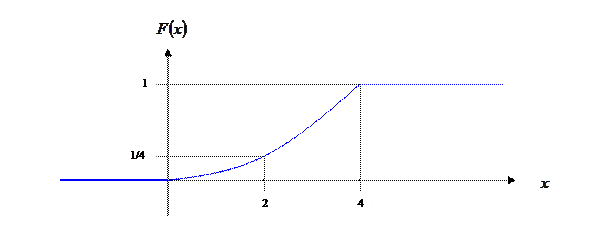
![]()
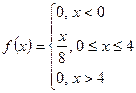
График плотности распределения ![]() представлен ниже.
представлен ниже.
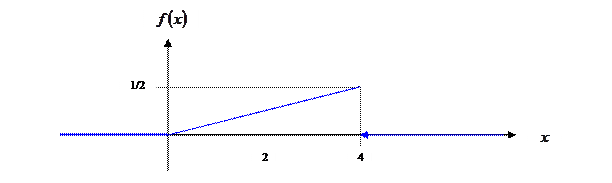
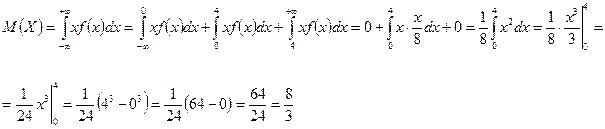
![]() математическое ожидание
математическое ожидание
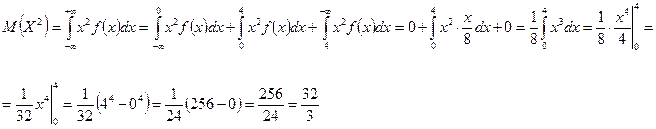
![]() дисперсия
дисперсия
![]()
Ответ.
![]()
![]()
![]()
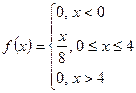
Похожие работы
-
Расчет математического ожидания и дисперсии
Определение математической вероятности правильного набора, если на нечетных местах комбинации стоят одинаковые цифры. Использование классического определения вероятности. Расчет математического ожидания и дисперсии для очков, выпавших на игральных костях.
-
Теория вероятностей и математическая статистика
Определение вероятности потери в ожесточенном бою одновременно глаза, рук, ноги; выбор возможных вариантов женитьбы; выигрыша, смерти. Расчет максимальной страховой риск компании и не оказаться в убытке.
-
Основы теории вероятности
Контрольная работа Основы теории вероятности Задание 1 Проверка выполнимости теоремы Бернулли на примере надёжности электрической схемы. Формулировка теоремы Бернулли: “Частота появления события в серии опытов сходится по вероятности к вероятности данного события.”
-
Контрольная работа по дисцеплине Прикладная математика
Министерство образования Республики Беларусь Учреждение образования «Витебский государственный технологический университет» Кафедра «Теоретической и прикладной математики»
-
Контрольная работа по Начертательной геометрии
Контрольная работа Задание № 1. Для фермы, изображённой на схеме: Посчитать степень статической определимости. Сделать проверку на мгновенную и геометрическую неизменяемости.
-
Теория вероятностей и математическая статистика
Определение вероятности случайного события; вероятности выиграшных лотерейных билетов; пересечения двух независимых событий; непоражения цели при одном выстреле. Расчет математического ожидания, дисперсии, функции распределения случайной величины.
-
Шпора по ТВИМС
Подбр.2 игральных кости. Найти вер-ть соб-й: 3 белых шара и 2 черных. Найти вер-ть Из колоды карт в 36 шт. достается 4 карты. Из ящика, содержащего 5 бел,2 черн,3 красн,
-
Задачи по Математике 3
Задача 1 Решить графическим методом задачу линейного программирования А) найти область допустимых значений многоугольник решений Б) найти оптимумы целевой функции
-
Элементы теории вероятностей 2
Введение. Если положить ручные механические часы на горизонтальную полку в середине её, то они будут лежать, но стоит их передвинуть к краю полки, то часы упадут. Это закон необходимого явления, вскрываемый в данном случае механикой. Но что произойдёт, когда часы упадут на пол? Останутся ли в целости или распадутся на n изуродованных частей? Обыватель это явление относит к случайности и не видит здесь закономерности.
-
Вероятность случайного события
Наступление случайного события в результате испытания, вообще говоря, нельзя предсказать заранее в принципе. Этот факт – непредсказуемость наступления – можно в некоторых случаях считать главным отличительным свойством случайного события.