Referat.me
/ / Формулы по математическому анализу

Название: Формулы по математическому анализу

Вид работы: реферат

Рубрика: Математика

Размер файла: 74.55 Kb

Скачать файл: referat.me-218554.docx

Краткое описание работы: Формулы дифференцирования Таблица основных интегралов Правила интегрирования Основные правила дифференцирования Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

Формулы по математическому анализу

Формулы дифференцирования Таблица основных интегралов



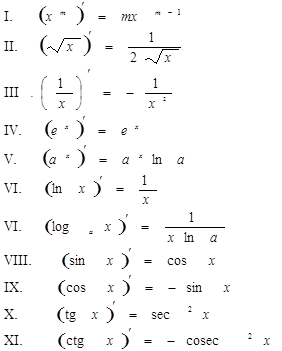
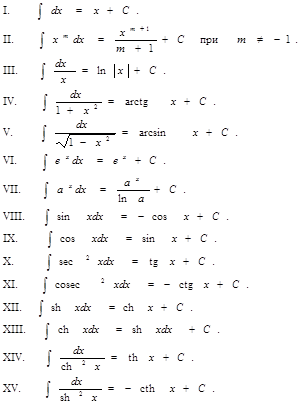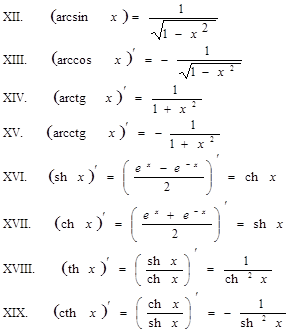
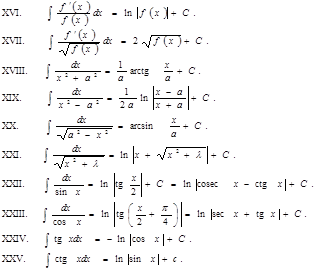Правила интегрирования


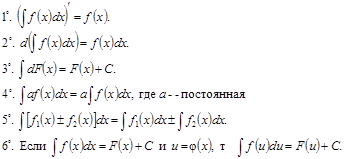Основные правила дифференцирования

Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

производные.


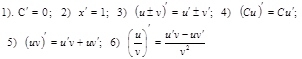7)


Интегрирование по частям Основные свойства

определённого интеграла


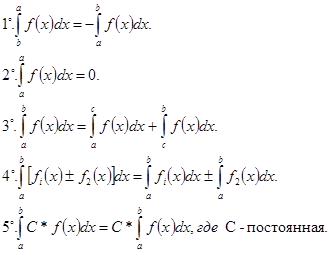Интегрирование простейших дробей


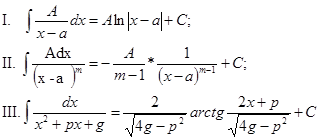Замена переменной в

неопределенном интеграле


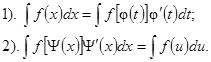
Площадь плоской фигуры

Площадь криволинейной трапеции, ограниченной кривой , прямыми и отрезком[a, b] оси Ox, вычисляется по формуле

Площадь фигуры, ограниченной кривыми и прямыми , находится по формуле

Если кривая задана параметрическими уравнениями , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми и отрезком[a, b] оси Ox, выражается формулой

где определяются из уравнений

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами находится по формуле

Длина дуги плоской кривой

Если кривая y=f(x) на отрезке [a, b] – гладкая (т.е. производная непрерывна), то длина соответствующей дуги этой кривой находится по формуле


При параметрическом задании кривой x=x(t), y=y(t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра , вычисляется по формуле


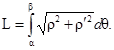Если гладкая кривая задана в полярных координатах уравнением , то длина дуги равна

Вычисление объема тела

1. Вычисление объема тела по известным площадям поперечных сечений.

Если площадь сечения тела плоскостью, перпендикулярной оси Ox, может быть выражена как функция от x, т.е. в виде , то объем части тела, заключенной между перпендикулярными оси Ox плоскостями x=a и x=b, находится по формуле

2. Вычисление объема тела вращения. Если криволинейная трапеция, ограниченная кривой и прямыми вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле


Если фигура, ограниченная кривыми и прямыми x=a, x=b, вращается вокруг оси Ox, то объем тела вращения

Вычисление площади поверхности вращения

Если дуга гладкой кривой вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле

Если кривая задана параметрическими уравнениями , то

Похожие работы

  • Формулы шпаргалка

    Предел функции: Число А наз-ся пределом функции f(x) в точке x0 если для всех x достаточно близких к x0, отличных от x0 значения ф-ии f(x) сколь угодно мало отличаются от числа A.

  • Производная дифференциал и интеграл

    КОНТРОЛЬНАЯ РАБОТА по высшей математике Содержание: 1. Пределы последовательностей и функций. 2 2. Производная и дифференциал. 3 3 Геометрические изложения и дифференцированные исчисления (построение графиков) 4

  • Основные правила дифференцирования

    Производные основных элементарных функций. Логарифмическое дифференцирование. Показательно-степенная функция и ее дифференцирование. Производная обратных функций. Связь между дифференциалом и производной. Теорема об инвариантности дифференциала.

  • Неопределенный интеграл

    Первообразная и неопределенный интеграл. Таблица интегралов. Некоторые свойства неопределенного интеграла. Интегрирование методом замены переменой или способом подстановки. Интегрирование по частям.

  • Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых)

    Лабораторная работа № 4. Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых). Гребенникова Марина 12-А класс Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

  • Дуальные числа

    Определение дуальных чисел. Свойства дуальных чисел. Функция и дифференциал функции. Аналог уравнений Коши-Римана. Оператор дифференцирования в области дуальных чисел.

  • Интегрирование и производная функций

    Осуществление интерполяции с помощью полинома Ньютона. Уточнение значения корня на заданном интервале тремя итерациями и нахождение погрешности вычисления. Применение методов Ньютона, Сампсона и Эйлера при решении задач. Вычисление производной функции.

  • Методы интегрирования

    Федеральное агентство по образованию Государственное общеобразовательное учреждение высшего профессионального образования Калмыцкий Государственный Университет

  • Высшая математика 4

    Контрольная работа высшая математика ЗАДАЧА 1. Вычислить пределы функций а) —д): а) 1. ► ► ► =-∞. Решение. Предел вычислен подстановкой

  • Контрольные билеты по алгебре

    Алгебра и начала анализа. 11 класс. Билет №1. Функция y = sin x, ее свойства и график. Показательная функция, ее свойства для случая, когда основание больше единицы (доказательство одного из свойств по желанию ученика).