Название: Алгоритмы численного решения задач
Вид работы: контрольная работа
Рубрика: Информатика и программирование
Размер файла: 79.21 Kb
Скачать файл: referat.me-134492.docx
Краткое описание работы: Графоаналитический метод решения задач. Получение задачи линейного программирования в основном виде. Вычисление градиента и поиск экстремумов методом множителей Лагранжа. Параболоид вращения функции. Поиск решения на основе условий Куна-Таккера.
Алгоритмы численного решения задач
Решить графоаналитическим методом.
Задача 1
maxj (X) = - 2x1 + x2 + 5x3
при 4x1 + 2x2 + 5x3 ³ 12
6x1 - 3x2 + 4x3 = 18
3x1 + 3x2 - 2x3 £ 16
Х ≥ 0
Здесь число n = 3 и число m = 3.
Выразим из ограничений и х3 :
![]() ≥ 0
≥ 0
Подставим его в целевую функцию
maxj (X) = ![]()
Получим новые ограничения:
![]()
![]()
![]()
х ≥ 0
Получили задачу линейного программирования в основном виде для n = 2
Вычисляем градиент ![]() :
:
![]() =
= ![]() =
= ![]()
|
|
|
|
|
|
|
|
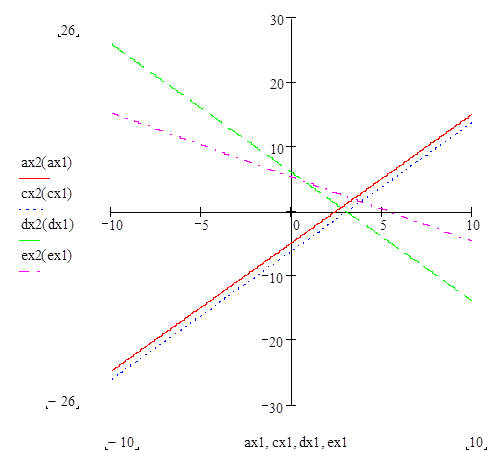
Рисунок 1
Прямые a, c, d и eпересекаются и образуют четырехугольник ACDE. Определим max φ (Х), который удовлетворяет условию Х>=0:
Это точка D (0,7; 4,7; 0).
Функция φ (Х* ) в точке D:
φ (Х* ) = 38,3
Найти экстремумы методом множителей Лагранжа
Задача 2
extr φ (X) = 4x1 - x2 2 - 12
при x1 2 + x2 2 = 25
Составим функцию Лагранжа:
L (X,λ) = 4x1 - x2 2 - 12 + λ (x1 2 + x2 2 - 25)
h (X) = x1 2 + x2 2 - 25 = 0 - функция ограничения.
Составим систему уравнений из частных производных и приравняем их нулю.
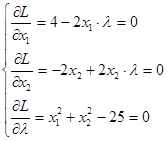
Решим данную систему уравнений:
2x2 ( λ- 1) = 0
Предположим, что x2 ≠ 0, тогда λ= 1 подставим в первое уравнение системы.
4 - 2x1 = 0
2x1 = - 4
x1 = 2
Подставим x1 в третье уравнение системы.
4 +x2 2 - 25 = 0
x2 2 - 21 = 0
x2 2 = 21
x2 = ±4,5826
Параболоид вращения функции h (x).
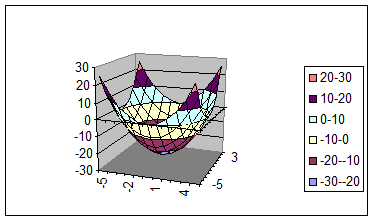
В двухмерной проекции график выглядит так:
|
|
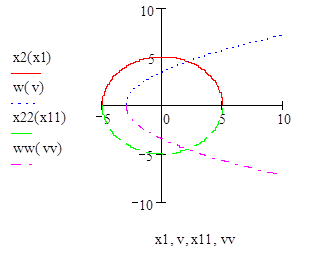
Рисунок 2.
На рис.2 видно, что в точках А1 и А2 функция φ (X) = h (X). В этих точках функция φ (X) равна минимальному значению.
(X* ,λ* ) N |
X1 * | X2 * | λ* | φ (X* ) | Примечание |
| 1 | 2 | 4,5826 | 1 | -24,25 | Min |
| 2 | 2 | -4,5826 | 1 | -24,25 | Min |
Решить обобщенным методом множителей Лагранжа или на основе условий Куна-Таккера.
Задача 3
extr φ (X) = 9 (x1
- 5) 2
+ 4 (x2
- 6) 2
= ![]()
при 3x1 + 2x2 >= 12
x1 - x2 <= 6
Решим задачу на основе условий Куна-Таккера.
Составим функцию Лагранжа.
L (X,λ) = ![]() + λ1
(3x1
+ 2x2
- 12) + λ2
(x1
- x2
- 6) =
+ λ1
(3x1
+ 2x2
- 12) + λ2
(x1
- x2
- 6) =
Составим систему уравнений из частных производных и приравняем их нулю.
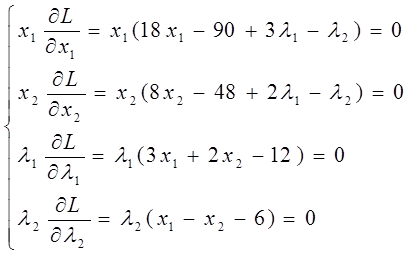
Решим систему уравнений.
1) Предположим, что λ2 ≠ 0, тогда из уравнения (d) получим
x2 = х1 - 6
Пусть λ1 = 0 и x1 ≠ 0, тогда из уравнения (а) получим
18x1 - 90 - λ2 = 0, λ2 = 18х1 - 90
Пусть x2 ≠ 0, тогда из уравнения (b) получим
8x2 - 48 - λ2 = 0
Подставив в уравнение выражения для x2 и λ2 , получим
x1 = 4
x2 = - 2
x1 * = 4; x2 * = - 2; φ (Х) * = 265
Трехмерный график целевой функции для данной задачи
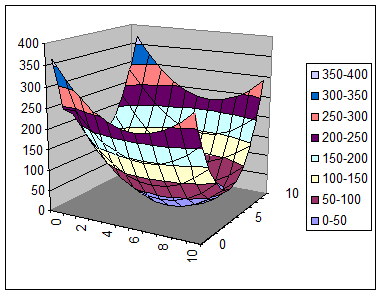
Двухмерная проекция
|
|
|
|
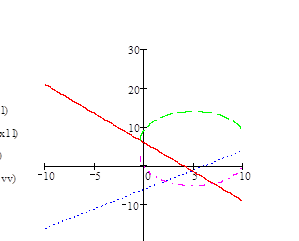
Рисунок 3
На рис.3 видно, что в точке А функция b (X) = a (X), которые находятся в параболоиде вращения целевой функции.
В этой точке функция φ (X) равна максимальному значению.
2) Предположим, что λ2 = 0 и x2 ≠ 0, тогда из уравнения (b) получим
8x2 - 48 + 2λ1 = 0
x2
= ![]()
x2
= 6 - ![]()
Предположим, что x1 ≠ 0, тогда из уравнения (а) выразим x1 .
18х1 - 90 + 3λ1 = 0
18 = 90 - 3λ1
х1
= ![]()
х1
= 5 - ![]()
Подставим выражения для x1 и x2 в уравнение (с) системы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
а) ![]() = 0, x1
= 5; x2
= 6
= 0, x1
= 5; x2
= 6
б) ![]() = 15
= 15
x1 = 2,5; x2 = 2,25
Подставив корни x1 = 5; x2 = 6 в целевую функцию получим φ (Х) = 0, а корни x1 = 2,5; x2 = 2,25 - получим φ (Х) = 112,49
Таким образом:
x1 * = 5; x2 * = 6; φ* (Х) = 0
На рис.4 видно, что в точке В функция φ (X) = a (X). В этой точке функция φ (X) равна минимальному значению.
|
|
|
|
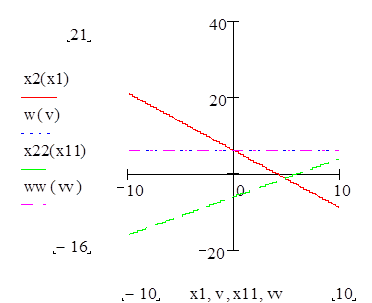
Рисунок 4
X* N |
X1 * | X2 * | φ (X* ) | Примечание |
| 1 | 5 | 6 | 0 | Min |
| 2 | 4 | -2 | 265 | Max |
Получить выражение вектор-функции и матрицы Якоби системы и составить алгоритм численного решения задачи на основе условий Куна-Таккера.
Задача 4
maxφ (X) = - x1 2 - x2 2 +2х2
при x1 + x2 >= 18
x1 + 2 x2 >= 14
Х>=0
Найдем выражение вектор-функции системы.
Составим функцию Лагранжа.
L (X,λ) = - x1 2 - x2 2 + 2х2 + λ1 (x1 + x2 - 18) + λ2 (x1 + 2x2 - 14)
Вектор-функция системы:
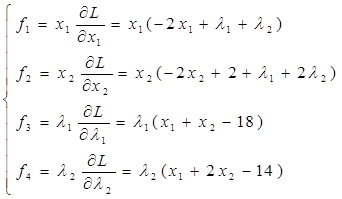
Составим матрицу Якоби.
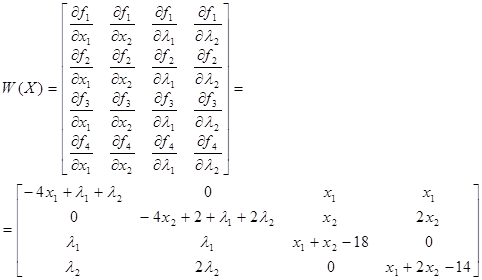
Составим алгоритм численного решения задачи:
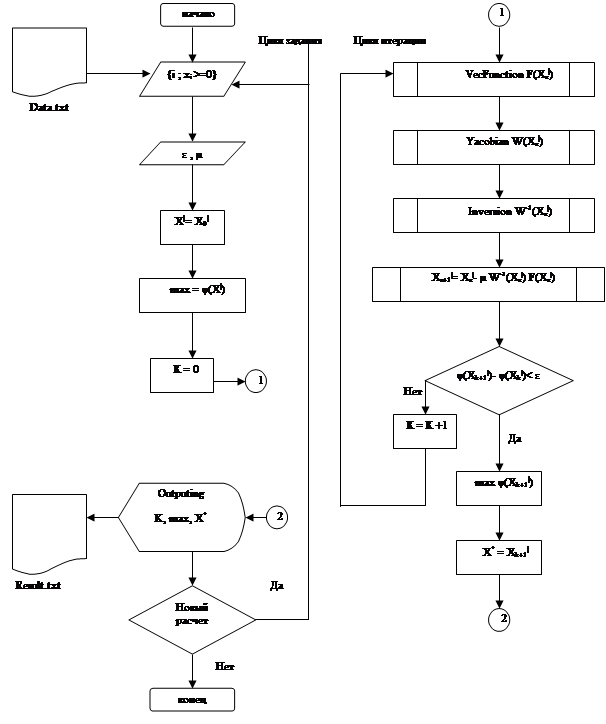
Рисунок 5.
Похожие работы
-
Формирование инвестиционного портфеля
Задача квадратичного программирования с параметром в правых частях ограничений и ее применение при формировании портфеля ценных бумаг.
-
Исследование устойчивости, решение задач линейного программирования графическим способом
Строение системы уравнений-ограничений и ее переменных, графический способ решения задач линейного программирования на плоскости. Выражение неизвестных через две независимые переменные, являющиеся координатными осями графика. Значение целевой функции.
-
Модели и методы принятия решения
Построение пространства допустимых решений. Нахождение оптимального решения с помощью определения направления убывания целевой функции. Нахождение оптимальной точки. Поиск экстремумов методом множителей Лагранжа. Условия экстремума Куна-Таккера.
-
Программа вычисления минимума заданной функции
Постановка задачи и ее формализация. Поиск значений интерполяционного многочлена в точках x1 и x2. Поиск минимума функции F(x) на отрезке [a;b]. Проверка условий сходимости методов. Тестирование программных модулей. Детализированная схема алгоритма.
-
Регрессионные зависимости
Вычисление значений регрессионно-авторегрессионной зависимости заданного выражения линейного программирования. Графическое представление математической модели в виде уравнения регрессии. Принципи оптимизации производственных и коммерческих операций.
-
Решение задач исследования операций
Целевая функция. Базисная переменная. Симплекс метод, таблица. Коэффициенты при свободных переменных в целевой функции. Задача квадратичного программирования, максимизации функции. Функция Лагранжа. Координаты стационарной точки. Система ограничений.
-
Приближенное вычисление значений определенного интеграла
Сущность и особенности применения метода средних треугольников. Порядок расчета по методу трапеций и Ньютона-Котеса. Формула Чебышева и значения узлов ее квадратуры. Составление блок-схемы программы и ее основных процедур различными численными методами.
-
Нелинейное программирование
Постановка задачи нелинейного программирования. Критерии оптимальности в задачах с ограничениями. Задачи с ограничением в виде равенств. Метод исключения переменных. Интерпретация условий Куна-Таккера. Функции нескольких переменных. Методы прямого поиска.
-
Математичне моделювання економічних систем
Задача лінійного програмування. Розв’язання задачі геометричним методом. Приведення системи рівнянь до канонічного вигляду. Розв’язання симплекс-методом. Розв’язок двоїстої задачі. Задача цілочислового програмування і дробово-лінійного програм.
-
Исследование операций
Математическая модель задачи. Система ограничений. Составление симплекс-таблиц. Разрешающий элемент. Линейное программирование. Коэффициенты при свободных членах. Целевая функция. Метод потенциалов, северо-западного угла. Выпуклость, вогнутость функции.