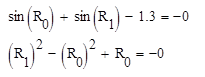Название: Інженерні розрахунки в MathCad
Вид работы: контрольная работа
Рубрика: Информатика и программирование
Размер файла: 194.07 Kb
Скачать файл: referat.me-135245.docx
Краткое описание работы: Розв’язання системи лінійних та нелінійних рівнянь у програмі MathCAD. Матричний метод розв'язання системи рівнянь. Користування панеллю інструментів Математика (Math) для реалізації розрахунків в системі MathCAD. Обчислення ітераційним методом.
Інженерні розрахунки в MathCad
Вступ
Тема контрольної роботи "Інженерні розрахунки в MathCad" з дисципліни "Інформатика".
Мета роботи - придбання навичок роботи з системою MathCad.
Завданні 1 передбачає розв’язання системи лінійних рівнянь у програмі MathCAD.
Завданні 2 передбачає розв’язання нелінійного рівняння за допомогою програми MathCAD.
Завданні 3 потребує знайти дійсні розв’язки системи нелінійних рівнянь із заданим ступенем точності в середовищі MathCAD.
Завдання
Завдання 1.
Задана система трьох лінійних рівнянь.
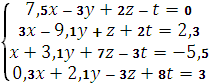
Знайти розв’язок системи матричним методом в середовищі MathCAD.
Розв’язання:
Розв’язання системи рівнянь у матричному виді проводиться за формулою
X=A-1 ×B,
деA - матриця, що складається з коефіцієнтів при невідомих,
А-1 - обернена матриця до матриці А,
B - вектор вільних членів,
X - вектор розв'язків системи.
Для реалізації розрахунків в системі MathCAD необхідно скористатися панеллю інструментів Математика (Math):
яка визивається командою View ® Toolbars ® Math :
mathcad інженерний розрахунок рівняння
Кнопками панелі Математика необхідно визвати панелі:
Калькулятор
(кнопкою ![]() ):
):
Матриця (
кнопкою ![]() ):
):

А потім виконати наступні дії: 1. Створимо матрицю А:
|
Пояснення до виконуваних дій: Використавши кнопку
Задаємо 4 рядки і 4 стовпці. А потім заповнюємо шаблон матриці коефіцієнтами системи:
|
2. Створюємо вектор В:
|
Задаємо 4 рядки 1 стовпець: Після чого заповнюємо маркери шаблону значеннями вільних членів системи:
|
3. Обраховуємо вектор Х:
|
Знак присвоєння: =
вибираємо на панелі Calculator
, обернену матрицю до матриці А
створюємо за допомогою кнопки |
4. Виводимо результат розрахунків:
|
Результати рішення системи: x = 0.091 y = - 0.243 z = - 0,601 t = 0.210 |
5. Робимо перевірку:
|
Розв’язок вірний, оскільки результат перемноження матриці А на вектор Х дорівнює вектору В. |
Завдання 2
Знайти корінь нелінійного рівняння x3 + sin (x - 3) +1 = 0 з точністю e =0.0001
Розв’язання:
Всяке рівняння з одним невідомим може бути записане у вигляді f (x) = 0.
Знаходження наближеного значення дійсних коренів рівняння складається з двох етапів:
1 етап - відділення коренів - виділення відрізка, що належить області існування функції f (x), на якому розташований один і тільки один корінь. Для відділення коріння будують графік функції f (x ). Абсциси точок перетину графіка функції y = f (x) з віссю ОХ і будуть наближеними значеннями коренів. По графіку легко вказати відрізки, на яких знаходиться один і тільки один корінь.
2 етап - уточнення наближених корінь, тобто обчислення їх із заданою точністю e.
1 етап. Графічне відділення коренів рівняння.
Побудуємо графік функції f (x) = x3 + sin (x - 3) +1.
Опишемо функцію в видіфункції користувача :
![]()
Вставимо в документ графічну область командою Insert ® Graph ® XY- Plot :
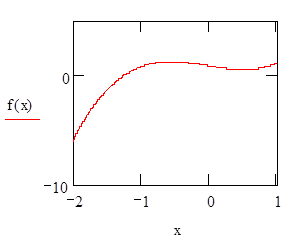
Маркери (-) отриманого шаблону заповнимо відповідно іменем аргументу х і іменем функції f (x):
Відформатуємо графік командою F ormat ® Graph ® XY-Plot :
Виберемо опцію Grossed (показувати осі координат):
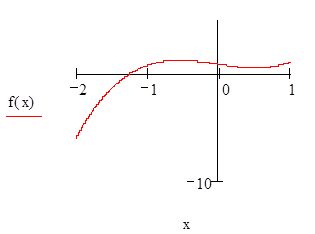
Як видно із графіка функція f (x) перетинає вісь абсцис на інтервалі [-2; - 1]. Для подальших розрахунків приймемо наближене значення кореня x = - 1
2 етап - уточнення кореня до точністі e =0.0001.
Уточнення кореня, тобто доведення його до заданого ступеню точності проведемо за допомогою функції root ( f ( x), x ).
Функція реалізує обчислення ітераційним методом, причому спочатку необхідно задати:
точність обчислень за допомогою системної змінної TOL;
початкове значення змінної х (будь-яке значення з відрізку визначеного на графіку).
Порядок дій: TOL: =0.0001 |
Пояснення: TOL - системна змінна, за допомогою якої задається точність обчислень в системі MathCAD. |
| x: = - 1 | Початкова умова, знайдена із графіка. |
x: = root (f (x), x) x= - 1.2361 |
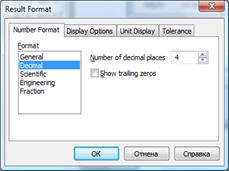
Застосування функції root для уточнення кореня. Вивід значенння уточненого кореня х . В установленому режимі MathCAD як правило виводить 3 десяткові знаки після коми. Оскільки задана точність e потребує 4 знаки, необхідно командою F ormat ®Result … в вікні ResultFormatзадати необхідне число знаків:
Отже корінь рівняння х = - 1,2361. |
Завдання 3
Розв’язати систему нелінійних рівнянь:
sin (x) + sin (y) - 1.3 = 0
y2 - x2 +x = 0
с точністю e=0.00001.
Розв’язання:
Відомо, що розв’язком системи є такі значення х і у , які перетворюють одночасно обидва рівняння в тотожності.
Для знаходження розв’язку системи необхідно спочатку графічно знайти грубе наближення цих значень для х і у .
Очевидно, що потрібно побудувати криві, які описуються рівняннями системи. Координати точки перетину цих кривих (як спільна їх точка) і являтимуть розв’язком системи.
Щоб побудувати ці криві необхідно рівняння системи привести до виду:
y= f1 ( x)
y= f2 ( x),
тобто в нашому випадку:
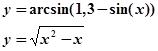 .
.
Після цього побудувати графіки функцій:
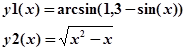 .
.
| Порядок дій: | Пояснення: |
Описуємо дві функції користувача
|
Функції asin , sin і Öвибрати з панелі Calculator. |
| Будуємо графіки функцій: y1 (x) і y2 (x) | |
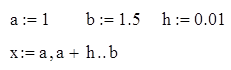 |
Довільно вибираємо відрізок [a,b], на якому будуємо графік функцій. Задаємо розбиття відрізку точками, описавши х як ранжовану змінну, яка змінюватиметься від а до b з кроком h . Якщо на вибраному відрізку [a,b] криві не перетнуться змінюмо до тих пір а і b поки не віднайдемо точку перетину. |
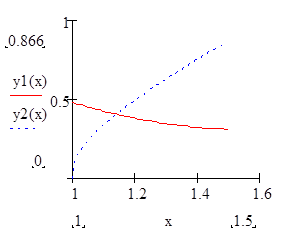 |
Із графіка приблизно знайти значення: х =1,2 і у = 0,4 координати точки перетинання графіків |
Задаємо початкові значення розвязку: x: =1.2 y: = 0.4 |
Задаємо початкові значення для х і у . |
| Задаємо точність обчислень | |
Уточнюємо розвязок до задоного ступеня точності.
|
Для уточнення розв’язку використовуємо блок рішення, який відкривається директивою G iven , а закривається функцією Find . В самому блоці записуються рівняння системи, в яких знак = вставляється з панелі
Вектору R присвоюється рішення системи. Отже х = 1,1413 і у = 0,4015. |
Проводимо перевірку розв’язку:
|
Перевірка розв’язку: Замість х і у підставляємо в рівняння R 0 і R1 , які являються елементами вектора R ( нумерація елементів починається з нуля). Оскільки справа отримали нулі - розв’язок задовольняє обидва рівняння. |
Література
1. Симонович С. Информатика: базовый курс. - СПб.: Питер, 1999, 640 с.
2. Дьяконов В. MATHCAD8/2000: специальный справочник - СПБ: Питер, 2001. - 592 с.
Похожие работы
-
Дослідження чисельних методів вирішення нелінійних рівнянь
В роботі розглянуто наближені методи розв'язку нелінійних рівнянь для методів Ньютона та хорд, складено блок-схеми та написано програму, за допомогою якої розв'язується задане рівняння. Аналіз рівняння, методів його розв'язання і результатів обрахунку.
-
Дослідження методів чисельного інтегрування
Характеристика основних методів чисельного інтегрування та розв’язання інтегралу методом Чебишева третього, четвертого та п’ятого порядків. Оцінка похибок та порівняння їх з точним обчисленнями отриманими в математичному пакеті Mathcad 2001 Professional.
-
Числові методи
Розв’язання системи рівняння методом Гауса за схемою з частковим вибором головного елементу. Рішення задачі Коші методом Рунге-Кутта. Знаходження моментів кубічних сплайнів методом прогонки. Розв’язування системи нелінійних рівнянь методом Ньютона.
-
Рішення задач з елементарної математики в пакеті MAPLE-8
Алгебраїчні перетворення в Maple за допомогою вбудованих функцій елементарних перетворень. Позбавлення від ірраціональності в знаменнику. Побудування графіку функції в пакеті Maple-8. Пакет plottools – пакет для створення та роботи з графічними об’єктами.
-
Наближені методи розв’язку нелінійних рівнянь
В роботі розглянуто наближені методи розв’язку нелінійних рівнянь. Для вказаних методів складено блок-схеми та написано програму, за якою розв’язується задане рівняння. Аналіз як самого рівняння і методів його розв’язання так і результатів обрахунку.
-
Розрахунок інтегралів за допомогою методів Гауса та Чебишева
Дослідження застосування різницевого методу для розв’язання крайової задачі. Дослідження проводиться на прикладі заданого диференційного рівняння. Дається опис методу та задачі в цілому. Застосування при обчисленні формули Чебишева і формули Гаусса.
-
Розв’язання нелінійних диференційних рівнянь методом січних і половинного ділення
Графічне зображення методу половинного ділення. Вибір методу інструментальних засобів вирішення задач. Розробка логічної частини програми для розв’язання нелінійного рівняння методами половинного ділення та січних. Особливість кодування на мові Паскаль.
-
Розв’язання задач з елементарної математики в пакеті Maple-8
Використання встроених функцій елементарних перетворень пакету Maple. Зображення основних геометричних фігур. Використання функції RootOf для позначення будь-якого кореня виразу, заданого як її параметр. Оператор виділення повного квадрату в чисельнику.
-
Рефакторинг. Виключення дублювання коду. Розробка бібліотек класів та знайомство з багатопроектними рішеннями
Розробка програми для розв’язання квадратних рівнянь з текстовим та графічним інтерфейсами користувача без дублювання їх коду. Алгоритм розв’язання квадратного рівняння у програмах з будь-яким інтерфейсом користувача, а саме: "консольний" та "форма".
-
Математичне моделювання економічних систем
Задача лінійного програмування. Розв’язання задачі геометричним методом. Приведення системи рівнянь до канонічного вигляду. Розв’язання симплекс-методом. Розв’язок двоїстої задачі. Задача цілочислового програмування і дробово-лінійного програм.
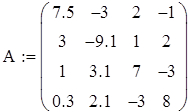
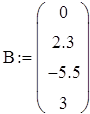
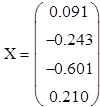
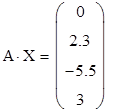
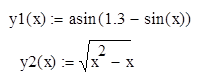
 .
.