Название: Быстродействующий адаптивный наблюдатель в системе компенсации неизвестного запаздывания
Вид работы: реферат
Рубрика: Информатика и программирование
Размер файла: 46.04 Kb
Скачать файл: referat.me-137599.docx
Краткое описание работы: Настоящая работа посвящена построению системы компенсации неизвестного запаздывания. Наличие большого запаздывания отрицательно сказывается на работоспособности системы управления.
Быстродействующий адаптивный наблюдатель в системе компенсации неизвестного запаздывания
БЫСТРОДЕЙСТВУЮЩИЙ АДАПТИВНЫЙ НАБЛЮДАТЕЛЬ В СИСТЕМЕ КОМПЕНСАЦИИ НЕИЗВЕСТНОГО ЗАПАЗДЫВАНИЯ
Настоящая работа посвящена построению системы компенсации неизвестного запаздывания. Наличие большого запаздывания, как известно [1], отрицательно сказывается на работоспособности системы управления.
Для компенсации неизвестного запаздывания разработана адаптивная система, состоящая из быстродействующего адаптивного наблюдателя, вычисляющего оценки неизвестных параметров и запаздывания системы управления, и прогнозатора Смита, компенсирующего это запаздывание.
Центральным моментом работы является построение алгоритма быстродействующего адаптивного наблюдателя для оценивания неизвестного запаздывания, так как прогнозатор Смита применим лишь в тех случаях, когда запаздывание априори известно. Этот алгоритм основан на использовании метода настраиваемой модели. Суть алгоритма изложена ниже.
Пусть поведение интересующего нас объекта описывается следующим дифференциальным уравнением:
![]() , (1)
, (1)
![]() ;
; ![]()
Здесь a1=3, a0=2 - известные постоянные коэффициенты; ![]() - неизвестные постоянные. Тогда структурная схема соответствующего процесса управления будет иметь вид, представленный на рис. 1. Здесь приборному измерению доступны вход xd(t) и выход x(t) системы управления.
- неизвестные постоянные. Тогда структурная схема соответствующего процесса управления будет иметь вид, представленный на рис. 1. Здесь приборному измерению доступны вход xd(t) и выход x(t) системы управления.
Построим быстродействующий адаптивный наблюдатель для идентификации неизвестных параметров системы ![]() , а также прогнозатор Смита для компенсации запаздывания
, а также прогнозатор Смита для компенсации запаздывания ![]() , после чего будем подставлять получаемые наблюдателем оценки
, после чего будем подставлять получаемые наблюдателем оценки ![]() в прогнозатор.
в прогнозатор.

![]()
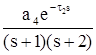
–
Рис 1. Система управления для объекта с неизвестным запаздыванием.
![]()
y(t)
v(t) –
![]() +
+
–
![]()
![]()
–

Рис. 2. Адаптивная система компенсации неизвестного запаздывания.
На каждом из подынтервалов времени функционирования системы Jj настраиваемую модель опишем следующими уравнениями:
![]()
![]() (2)
(2)
![]() ,
,
где ![]() - параметры модели, настраиваемые соответственно на параметры
- параметры модели, настраиваемые соответственно на параметры ![]() объекта (1).
объекта (1).
Введем ошибку e(t) = x(t) - y(t).
Конечная структурная схема системы управления с адаптивным наблюдателем и прогнозатором Смита показана на рис. 2.
Система уравнений для выходного сигнала прогнозатора Смита v(t) и входного сигнала объекта, прогнозатора и наблюдателя u(t):
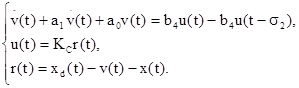
Уравнение для ошибки e(t) будет иметь вид (вычитаем (2) из (1) и линеаризуем правую часть):
![]() , (3)
, (3)
где ![]()
![]()
Приведем (3) к системе уравнений первого порядка. Положим
![]()
![]()
Тогда в векторной форме уравнение (3) будет иметь вид
![]()
![]()
![]() +
+![]()
![]() (4)
(4)
или в краткой форме
![]() ,
,
где![]() ,
, ![]() , A=
, A=![]() , Z=
, Z= ![]() .
.
Решением (4) будет
![]()
![]()
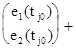
![]()
![]() (5)
(5)
или в краткой форме
![]()
где Ф(t)= ![]() , R(t)=
, R(t)= ![]() - решения уравнений
- решения уравнений
![]() (6)
(6)
![]() . (7)
. (7)
Перепишем первую строку системы (5) в виде
![]() (8)
(8)
где
![]()
![]()
![]() .
.
Здесь w(t) и ![]() - известные величины для любого t; вектор g содержит неизвестные параметры объекта, а векторы bj (j=0,l,...,N-l) являются функциями перестраиваемых параметров эталонной модели
- известные величины для любого t; вектор g содержит неизвестные параметры объекта, а векторы bj (j=0,l,...,N-l) являются функциями перестраиваемых параметров эталонной модели ![]() .
.
Набирая данные на каждом из подынтервалов Jj в моменты времени tj1,...,tjm, образуем из (8) алгебраическую систему вида
![]()
или в матричной форме
![]() (9)
(9)
Число m выбирается так, чтобы уравнений в (9) было не меньше числа неизвестных параметров. В данном случае m больше или равно 3.
Решение алгебраической системы (9) при этом записывается в виде
![]() (10)
(10)
где ![]() - псевдообратная матрица.
- псевдообратная матрица.
Изменение параметров bj при переходе от подынтервала Jj к Jj+1 осуществляется по рекуррентной формуле
![]() , (11)
, (11)
где L=diag(l1,....,l3) - вещественная диагональная матрица, все числа li>0. Можно показать [2], что этот процесс перестройки параметров сходится экспоненциально, т.е. значения перестраиваемых параметров модели ![]() сходятся к значениям неизвестных параметров объекта
сходятся к значениям неизвестных параметров объекта ![]() .
.
Таким образом, для того, чтобы идентифицировать постоянные неизвестные параметры ![]() объекта (1), параметры настраиваемой модели (2)
объекта (1), параметры настраиваемой модели (2) ![]() следует изменять с помощью алгоритма, который описывается уравнениями (6)-(11).
следует изменять с помощью алгоритма, который описывается уравнениями (6)-(11).
Было проведено численное моделирование этой системы на ЭВМ в среде MATLAB 5.2. Результаты компьютерного моделирования подтверждают эффективность разработанного алгоритма.
Предлагаемый алгоритм адаптивного наблюдателя обладает важными для практики свойствами: заданной длительностью переходного процесса по параметрам и запаздыванию; отсутствием взаимного влияния переходных процессов настройки в разных параметрических каналах и практической независимостью времени переходных процессов по параметрам и запаздыванию от изменения амплитуды входных и выходных сигналов.
Список литературы
[1] Гурецкий X. Анализ и синтез систем управления с запаздыванием. Пер. с польского. - М.: Машиностроение, 1974.
[2] Копысов О.Ю., Прокопов Б.И. Построение алгоритма перестройки параметров и запаздывания в методе настраиваемой модели. М.: МГИЭМ, 1999.
3. А.В. Старосельский, Московский Государственный Институт Электроники и Математики, быстродействующий адаптивный наблюдатель в системе компенсации неизвестного запаздывания
Похожие работы
-
Радиорелейная связь: организация дальней связи
В России наиболее широкое распространение получили две технологии построения транспортной инфраструктуры оператора связи: на основе волоконно-оптических систем и на основе систем радиосвязи.
-
Эволюционное моделирование некоторых систем с сосредоточёнными параметрами
В проблемах прогноза и оценки социальных, экологических, экономических мероприятий часто нужно моделировать динамику взаимодействия системы с его окружением (по обмену ресурсами).
-
Автоматическая система регулирования вязкости топлива
1. Описание устройства и взаимодействие элементов САР Измеритель вязкости и пневмопреобразователь мотора вращает с постоянной скоростью ведущий диск
-
Cинтез систем
Введение Управление каким-либо объектом – это процесс воздействия на него с целью обеспечения требуемого течения процессов в объекте или требуемого изменения его состояния. Основой управления является переработка информации о состоянии объекта в соответствии с целью управления.
-
Устройство современных модемов
Общие сведения. Состав модема для КТСОП. Скремблирование. Эхо подавление.
-
Дискретные сигналы
Дискретизация непрерывных сигналов. Связь спектров дискретного и непрерывного сигналов. Преобразование Фурье и Лапласа для дискретных сигналов.
-
Дискретные цепи
Разностное уравнение и дискретная цепь. Передаточная функция дискретной цепи. Общие свойства передаточной функции. Частотные характеристики. Импульсная характеристика. Свертка.
-
Численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу
Постановка задачи, математические и алгоритмические основы решения системы линейных алгебраических уравнений. Решение системы данных уравнений методом Гаусса с выбором главного элемента по столбцу. Функциональные модели и блок-схемы решения задачи.
-
Принципы построения систем автоматического управления
Теория автоматического управления как наука, предмет и методика ее изучения. Классификация систем автоматического управления по различным признакам, их математические модели. Дифференциальные уравнения систем автоматического управления, их решения.
-
Метод Гаусса для расчета электрических цепей
Разработка алгоритма составления системы уравнений при помощи законов Кирхгофа по определенной электрической схеме. Приложение для решения данной системы методом Гаусса с выбором ведущего элемента по строке. Описание программы, руководство пользователя.