Название: Построение графиков функций. Решение нелинейных уравнений и систем нелинейных уравнений
Вид работы: контрольная работа
Рубрика: Информатика и программирование
Размер файла: 67.56 Kb
Скачать файл: referat.me-140209.docx
Краткое описание работы: Методика и основные этапы построения ранжированных переменных, сферы и особенности их практического применения. Порядок построения графиков в декартовой системе. Приведение примеров решение нелинейных уравнений и их систем при помощи решающего блока.
Построение графиков функций. Решение нелинейных уравнений и систем нелинейных уравнений
Введение
Тема контрольной работы «Построение графиков функций. Решение нелинейных уравнений и систем нелинейных уравнений » по дисциплине «Информатика».
Цель и задачи работы:
1. Научиться создавать и применять ранжированные переменные.
2. Научиться строить графики в декартовой системе.
3. Научиться решению нелинейных уравнений и систем нелинейных уравнений с помощью решающего блока.
4. Решение системы линейных уравнений матричным способом.
При решении многих технических задач математические модели решения представляют собой нелинейные уравнения, системы нелинейных уравнений, системы линейных уравнений.
Уравнения и системы уравнений, возникающие в практических задачах, обычно можно решить только численно. Методы численного решения реализованы и в программе MathCad.
Для выполнения практической части:
Загрузить программу MathCADс помощью ярлыка.
Сохранить файл в собственной папке под именем ….
Задание №1
Создать ранжированные переменные и вывести таблицы их значений
1. Создать ранжированную переменную z , которая имеет:
начальное значение 1
конечное значение 1.5
шаг изменения переменной 0.1
и вывести таблицу значений переменнойz
2. Создать ранжированную переменную y , которая имеет:
начальное значение 2
конечное значение 7
шаг изменения переменной 1
и вывести таблицу значений переменной y
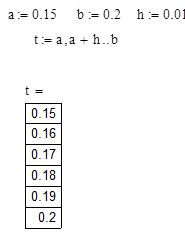
3. Создать ранжированную переменную t, которая имеет:
начальное значение a
конечное значение b
шаг изменения переменной h
и вывести таблицу значений переменнойt
Для создания ранжированных переменных используют Палитру
|
Последовательность действий: 1.
2. (запятая) 3. ввести следующее значение (1.1) 4.
нажимают кнопку 5. 1.5 (ввести конечное значение |
(ввести начальное значение)
Если шаг изменения =1, то не выполняют пункты 2. и 3.
Для вывода таблицы значений, достаточно ввести имя переменной и знак 
.
Выполнение Задания № 1
| 1.1 | 1.2 | 1.3 |
 |
 |
 |
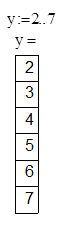Задание ранжированной переменной в виде  удобно
тем, что изменяя значения a, h, bавтоматически изменяется и таблица вывода ранжированной переменной |
||
Задание №2
Построить график функции
f ( x )= sin ( x )+ ex -2 на диапазоне [-5; 2 ]
Выполнение задания № 2
Последовательность действий:
1. Создать ранжированную переменную x
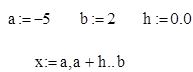
2. Создать функцию пользователя 
3. Для построения графика использовать Палитру Graph и кнопку |
|
4. Ввести в место ввода по оси X имя независимого аргумента – x
5. Ввести в место ввода по оси Y – f ( x )
6. Отвести от графика указатель мыши и щелкнуть левой кнопкой мыши. График будет построен
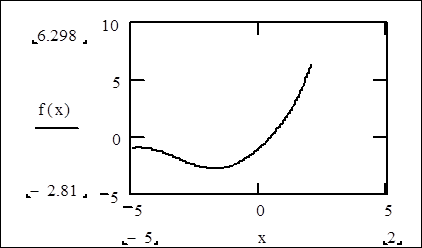
Рис. 1.1
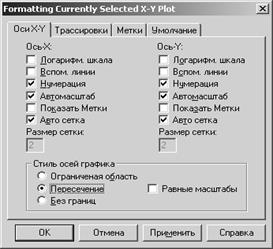
Для форматирования графика, дважды щелкнуть в области графика.
Появится диалоговое окно
|
В этом окне 1.на Вкладке Ось X - Y установитьпереключатель Пересечение 2.на Вкладке Трассировки можно установить цвет и толщину линии |
Если щелкнуть по графику (появятся маркеры вокруг графика), то методом протягивания в нужном направлении можно изменить размеры графика.
Так выглядит график после форматирования
Рис. 1.2
Теоретическая часть
Блок уравнений и неравенств, требующих решения, записывается после ключевого слова Given (дано ). При записи уравнений используется знак логического равенства = , кнопка находится в Палитре Boolean.
Заканчивается блок решения вызовом функции Find(найти ). В качестве аргументов этой функции – искомая величина. Если их несколько (при решении систем уравнений, то искомые неизвестные должны быть перечислены через запятую).
Всякое уравнение с одним неизвестным может быть записано в виде, f(x)=0,
где f(x) – нелинейная функция. Решение таких уравнений заключается в нахождении корней, т.е. тех значений неизвестного x , которые обращают уравнение в тождество. Точное решение нелинейного уравнения далеко не всегда возможно. На практике часто нет необходимости в точном решении уравнения. Достаточно найти корни уравнения с заданной степенью точности.
Процесс нахождения приближенных корней уравнения состоит из двух этапов:
1 этап. Отделение корней, т.е. разбиения области определения функции f(x), на отрезки, в каждом из которых содержится только один корень уравнения.
2 этап.Уточнение приближенных корней уравнения, т.е. доведение их до заданной степени точности.
Практическая часть
Задание №1
Постановка задачи:
Найти корень уравнения x 3 - x 2 =2 с точностью Е=0,00001
Приведем заданное уравнение к виду f ( x ) =0
x 3 - x 2 -2 =0 f ( x ) = x 3 - x 2 -2
Выполнение задания № 1
1 этап – отделение корней
 |
Создать функция пользователя |
 |
Создать ранжированную переменную x |
 |
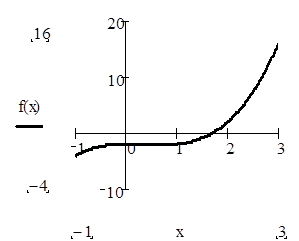Построить график f(x) |
Из графика видно, что приближенное значение x =1.5 (то значение x, при котором функция пересекает ось x)
2 этап – уточнение приближенного значения корня
Специальный вычислительный блок имеет следующую структуру |
|
 |
Задают начальное значение x (из графика – приближенное) |
 |
TOL– Системная переменная, которой присваивается значение требуемой точности 0.00001 |
Так как требуемая точность вычисления 0.00001, то дважды щелкнув по результату, необходимо отформатировать результат (задать нужное количество десятичных знаков).
| Given | Given (дано ) – ключевое слово, открывающее блок решения |
| x3 -x2 –2 = 0 | Так записывается уравнение. При записи уравнений в решающем блоке используют знак логического равенства =
, которому соответствует кнопка  Палитры  |
 |
Вызвать функции Find, которая в качестве аргументов должна содержать искомую величины (если их несколько, то они перечисляются через запятую) |
Ответ: x =1.69562
Проверка :
Найденное значение корня подставим в заданное уравнение.
Если xнайден верно, то f(x)=0 (так как мы ищем приближенное значение, то в правой части может быть не нуль, а очень малое значение < Е (требуемой точности)
Уточнение корня в программе MathCad
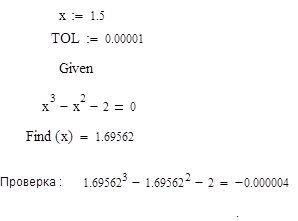
Задание №2
Постановка задачи:
Решить систему уравнений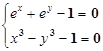 
с точностью Е=0.00001
Выполнение задания № 2
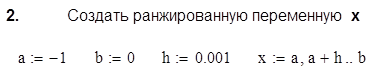
3. Построить графики функций y1 (x) и y2 (x)
4. Находим из графика точку пересечения кривых
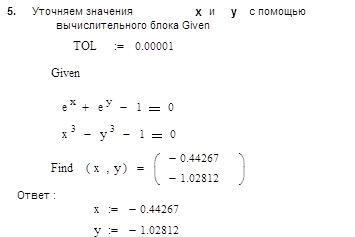
Проверка:
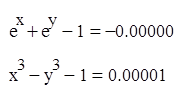
Литература
1. Симонович С. Информатика: базовый курс. – СПб.: Питер, 1999, 640 с.
2. Дьяконов В. MATHCAD 8/2000: специальный справочник – СПБ: Питер, 2001. – 592 с.
Похожие работы
-
ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения дифференциального уравнения n-го порядка
Решение дифференциального уравнения N-го порядка методом интегрирования при помощи характеристического уравнения, методом интегрирования и операторным методом для значений аргументов при заданных начальных условиях и нулевых уравнения 4–го порядка.
-
Решение нелинейных уравнений
ЧИСЛЕННОЕ . 1п. Общий вид нелинейного уравнения F(x)=0 Нелинейные уравнения могут быть двух видов: Алгебраические anxn + an-1xn-1 +… + a0 = 0 Трансцендентные- это уравнения в которых х является аргументом
-
Решение системы нелинейных уравнений
Теоретическая часть. В данной расчетно-графической работе (далее РГР) требуется составить программу для решения системы нелинейных уравнений методом последовательной итерации
-
Расчетно-графическая работа
§1. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ. 1п. Общий вид нелинейного уравнения F(x)=0 Нелинейные уравнения могут быть двух видов: Алгебраические
-
Исследование устойчивости, решение задач линейного программирования графическим способом
Строение системы уравнений-ограничений и ее переменных, графический способ решения задач линейного программирования на плоскости. Выражение неизвестных через две независимые переменные, являющиеся координатными осями графика. Значение целевой функции.
-
Моделирование структурных схем в среде SIMULINK пакета MATLAB
Практические навыки моделирования структурных схем в среде SIMULINK пакета MATLAB. Построение графиков функций в декартовой системе координат. Решение систем линейных и нелинейных уравнений. Работа с блоками Sum, Algebraic Constraint, Gain, Product.
-
Итерационные методы решения нелинейных уравнений
Решение нелинейных уравнений методом простых итераций и аналитическим, простым и модифицированным методом Ньютона. Программы на языке программирования Паскаль и С для вычислений по вариантам в порядке указанных методов. Изменение параметров задачи.
-
Работа с массивами и решение систем уравнений в Mathcad
Использование ранжированных переменных в программном пакете Mathcad. Создание матриц без использования шаблонов матриц, описание операторов для работы с векторами и матрицами. Решение систем линейных и нелинейных уравнений с помощью функций Mathcad.
-
Решение систем нелинейных уравнений методом Бройдена
Решение нелинейных краевых задач. Входные данные и содержание алгоритма Бройдена. Содержание алгоритма Бройдена. Метод исключения Гаусса для решения СЛАУ. Вывод формулы пересчета Бройдена. Разработка программы, исследование результата и примеры ее работы.
-
Решение систем нелинейных алгебраических уравнений методом Ньютона
Модифицированный метод Ньютона при заданных начальных условиях, где задаётся погрешность вычисления. Вычисления корня уравнения при помощи программы. Построения графика зависимости приближений двух координат, при котором задаются промежутки и константы.