Referat.me / Транспорт / Задача по Транспорту

Название: Задача по Транспорту

Вид работы: реферат

Размер файла: 67.51 Kb

Скачать файл: referat.me-337613.docx

Краткое описание работы: Исходные данные. Постановка транспортной задачи. Имеется четыре поставщика и четыре потребителя. Пусть Ai- i-й поставщик, ai – запас продукта у i-го поставщика, i=1,2,3,4;

Задача по Транспорту

2. Исходные данные.

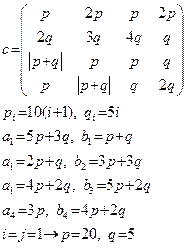
3. Постановка транспортной задачи.

Имеется четыре поставщика и четыре потребителя.

Пусть A_i - i-й поставщик, a_i – запас продукта у i-го поставщика, i=1,2,3,4;

B_j - j-й потребитель, b_j – потребность в продукте j-го потребителя, j=1,2,3,4.

№ поставщика/потребителя	Запасы продукции (а_i )	Потребность в продукции(b_j )
1	115	25
2	45	75
3	90	110
4	60	90
Общий запас продукции/ Общий объем потребностей	310	300

Матрица транспортных затрат имеет вид:

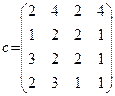
Необходимо найти оптимальный план перевозок, при котором суммарные затраты на транспортировку будут минимальными.

4. Соотношение “потребности-возможности” и переход к сбалансированной задаче.

Т.к. общий запас продукции у всех поставщиков () на 10 единиц больше, чем cуммарный объем потребностей в продукции всех потребителей (), т.е. выполняется неравенство a>b, значит, наблюдается избыток продукции у поставщиков и мы имеем дело с несбалансированной задачей.

Для того чтобы впоследствии иметь возможность составить верную экономико-математическую модель (ЭММ), необходимо привести задачу к сбалансированному виду. Для этого введем фиктивного (дополнительного) потребителя- B₅ , который и будет потреблять излишек продукции- (b₅ =a-b).

Теперь выполняется следующее равенство и задачу можно считать сбалансированной. При этом затраты на доставку продукции новому потребителю равны нулю.

При применении результатов задачи на практике, количество продукции, доставленной фиктивному потребителю, трактуется как остатки продукции на складе.

5. ЭММ сбалансированной транспортной задачи.

Пусть x_ij - количество продукции, перевозимой от поставщика A_i потребителю B_j , а матрица

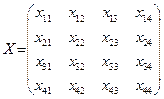-план перевозки.

Рассмотрим произвольного i-го поставщика A_i :

- это означает, что общее количество продукции, поставляемое i-тым поставщиком всем потребителям должно быть равно суммарным запасам поставщика(т.е. поставщик поставляет всю продукцию – принцип сбалансированной задачи).

Рассмотрим произвольного j-го потребителя B_j :

- это означает, что общее количество продукции, получаемое j-тым потребителем от всех поставщиков должно быть равно общим потребностям потребителя (т.е. потребитель получает всю желаемую продукцию – принцип сбалансированной задачи).

Также необходимо помнить, что целью задачи является уменьшение суммарных затрат на перевозку, т.е.

Совокупность 1),2),3) и является ЭММ транспортной задачи, запишем ее в развернутом виде:

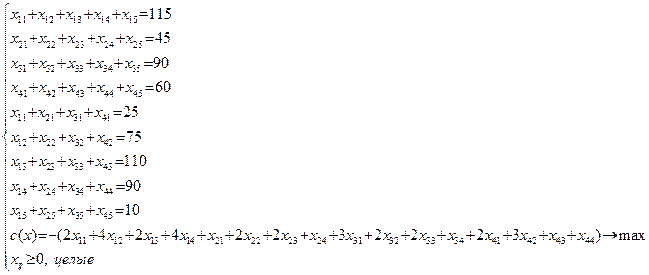
Запишем технологическую матрицу для данной модели:

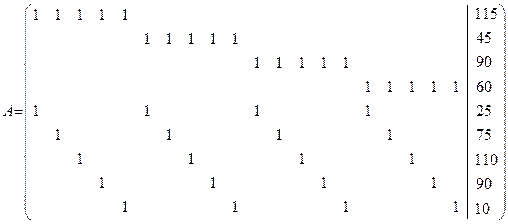
6. Решение транспортной задачи.

5.1. Нахождение базисного плана перевозок.

Найдем базисный план перевозок методом минимальных затрат, для этого построим матричную модель данной задачи.

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10
a1=115	²	⁴ 55	² 50	⁴	⁰ 10
a2=45	¹ 25	²	²	¹ 20	⁰
a3=90	³	² 20	²	¹ 70	⁰
a4=60	²	³	¹ 60	¹	⁰

Для того чтобы определить, является ли данный план перевозок базисным, необходимо проверить, выполняются ли следующие условия:

- число положительных перевозок не больше (m+n-1), где m- количество поставщиков, n- количество потребителей;

- отсутствие циклов.

Оба условия выполняются, более того, количество положительных перевозок (N=8) равно (m+n-1=8), а, значит, данный план перевозок является базисным невырожденным.

5.2. Проверка базисного невырожденного плана перевозок на оптимальность.

Проверка базисного невырожденного плана перевозок на оптимальность производится при помощи следующей теоремы (следствия из теоремы равновесия):

пусть- план транспортной задачи,

если числа - потенциалы потребителей и - потенциалы поставщиков определяются так, что:

2) (2)

то x* является оптимальным планом перевозок.

Пусть потенциал первого поставщика равняется нулю (U1=0) рассчитаем оставшиеся потенциалы потребителей и поставщиков по формуле (2).

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10	Ui
a1=115	²	⁴ 55	² 50	⁴	⁰ 10	0
a2=45	¹ 25	²	²	¹ 20	⁰	2
a3=90	³	² 20	²	¹ 70	⁰	2
a4=60	²	³	¹ 60	¹	⁰	1
Vj	3	4	2	3	0

Проверим выполнение неравенств (1)

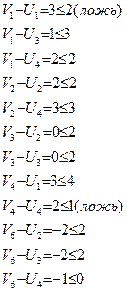
Признак оптимальности нарушается, следовательно, план не является оптимальным. Рассмотрим клетки (1;1) и (4;4). Для обеих неравенство не выполняется и .

5.3. Введение новой положительной перевозки z .

Изменим план перевозок так, что первый поставщик поставляет продукцию первому потребителю:

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10
a1=115	² z	⁴ 55	² 50	⁴	⁰ 10
a2=45	¹ 25	²	²	¹ 20	⁰
a3=90	³	² 20	²	¹ 70	⁰
a4=60	²	³	¹ 60	¹	⁰

Необходимо отметить, что в результате произведенных преобразований появляется цикл , который необходимо разрушить. Для этого, обходя цикл, будем вычитать или добавлять “z”, т.е.

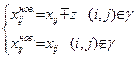
и тогда матричная модель задачи примет вид:

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10
a1=115	² ^z	⁴ 55-z	² 50	⁴	⁰ 10
a2=45	¹ 25-z	²	²	¹ 20+z	⁰
a3=90	³	² 20+z	²	¹ 70-z	⁰
a4=60	²	³	¹ 60	¹	⁰

Примем z=25, т.к. именно при этом значении z все положительные перевозки имеют знак «+» и заново рассчитаем потенциалы потребителей и поставщиков.

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10	Ui
a1=115	² 25	⁴ 30	² 50	⁴	⁰ 10	0
a2=45	¹ 0	²	²	¹ 45	⁰	2
a3=90	³	² 45	²	¹ 45	⁰	2
a4=60	²	³	¹ 60	¹	⁰	1
Vj	2	4	2	3	0

В результате проверки нового плана на оптимальность оказалось, что первый признак оптимальности не выполняется только для клетки (4,4), т.е.

Введем новую положительную перевозку z от четвертого поставщика четвертому потребителю:

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10
a1=115	² 25	⁴ 30	² 50	⁴	⁰ 10
a2=45	¹	²	²	¹ 45	⁰
a3=90	³	² 45	²	¹ 45	⁰
a4=60	²	³	¹ 60	¹ z	⁰

Необходимо разрушить появившийся цикл , поэтому, обходя цикл, будем вычитать или добавлять “z”, тогда матричная модель примет вид:

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10
a1=115	² 25	⁴ 30-z	² 50+z	⁴	⁰ 10
a2=45	¹	²	²	¹ 45	⁰
a3=90	³	² 45+z	²	¹ 45-z	⁰
a4=60	²	³	¹ 60-z	¹ z	⁰

Примем z=30 и проверим новый базисный план на оптимальность:

b=310 a=310	b1=25	b2=75	b3=110	b4=90	b5=10	Ui
a1=115	² 25	⁴ 0	² 80	⁴	⁰ 10	0
a2=45	¹	²	²	¹ 45	⁰	1
a3=90	³	² 75	²	¹ 15	⁰	1
a4=60	²	³	¹ 30	¹ 30	⁰	1
Vj	2	3	2	2	0

В данном случае оба признака оптимальности выполняются, следовательно, этот базисный план является оптимальным.

6. Результаты.

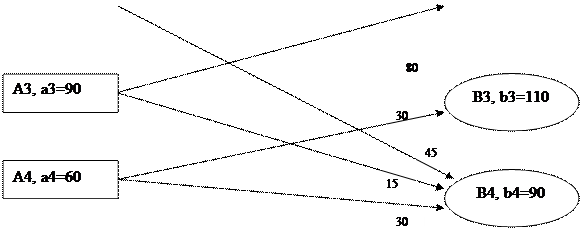
Итак, оптимальный план перевозок, при котором минимизируются затраты на транспортировку имеет вид:

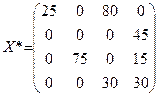
Также необходимо помнить, что пятый потребитель является фиктивным, и объем его потребности в продукции(10)- это то количество продукции, которое останется на складе.

Общие затраты на перевозку находятся по формуле, приведенной в начале работы при помощи данных итоговой матричной модели.

A4; a4=60

C*= 2*25+2*80+45+2*75+15+30+30+10*0=50+160+45+150+75=480

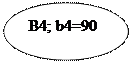
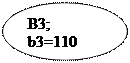
Также итоговый план перевозок можно представить в виде следующей схемы:

A2, a2=45

Задача по Транспорту

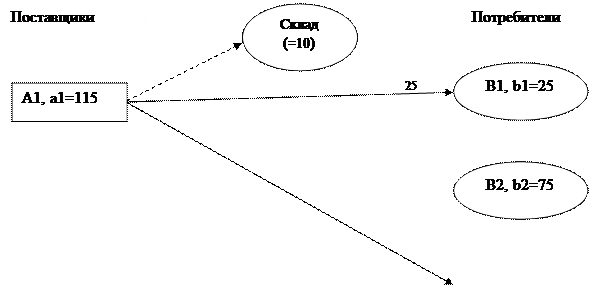
Похожие работы