Название: Расчетно-графическое обоснование прямого стержня
Вид работы: контрольная работа
Рубрика: Строительство
Размер файла: 527.99 Kb
Скачать файл: referat.me-333977.docx
Краткое описание работы: Задача 1.1. Расчет прямого ступенчатого стержня Исходные данные: F1, кН F4, кН F6, кН L1, см L2, см L3, см A1, см2 A2, см2 A2, см2 Построить эпюры продольных сил, напряжений и перемещений;
Расчетно-графическое обоснование прямого стержня
Задача 1.1. Расчет прямого ступенчатого стержня

Исходные данные:
| F1 , кН | F4 , кН | F6 , кН | L1 , см | L2 , см | L3 , см | A1 , см2 | A2 , см2 | A2 , см2 |
| 160 | 60 | 100 | 64 | 36 | 44 | 8 | 6 | 4 |
1) Построить эпюры продольных сил, напряжений и перемещений;
2) Оценить прочность стержня
1) С целью определений значений продольных сил в различных сечениях выделим характерные сечения трехступенчатого стержня, в которых найдем продольные силы. И построим эпюру продольных сил.

1. Сечение 1–1
![]()
![]()
![]() кН
кН
2. Сечение 2–2
![]()
![]()
![]() кН
кН
3. Сечение 3–3
![]()
![]()
![]() кН
кН
4. Сечение 4–4
![]()
![]()
![]() кН
кН
5. Сечение 5–5
![]()
![]()
![]() кН
кН
2) На основании найденных значений продольных сил в характерных сечениях стержня строим эпюру продольных сил. Нормальные напряжения в тех же сечениях определим по формуле:
![]() .
.
И построим эпюру напряжений.
![]() мПа
мПа
![]() мПа
мПа
![]() мПа
мПа
![]() мПа
мПа
![]()
3) Вычислим деформации отдельных участков стержня по формуле:
![]()
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]() мм
мм
![]()
4) Найдем характерные перемещения стержня и построим их эпюры
![]() мм
мм
![]() мм
мм
![]() =6 мм
=6 мм
![]() +
+
![]() =11 мм
=11 мм
![]() +
+
![]() =11 мм
=11 мм
5) Прочность материала стержня проверим в сечении, где наибольшее напряжение
![]()
Следовательно, перенапряжение материала составляет:
![]()

Задача 1.2. Геометрические характеристики плоских фигур
Для составного сечения необходимо определить:
1) Положение центра тяжести
2) Осевые и центробежные моменты инерции относительно центральных осей
3) Положение главных центральных осей
4) Вычислить значения главных центральных моментов инерции
5) Построить круг инерции и по нему проверить положение главных центральных осей и значения главных центральных моментов инерции
6) Вычертить сечение в удобном масштабе и показать все необходимые оси и размеры
Исходные данные:
| A, см2 | Ix , см4 | Iy , см4 | Dxy , см4 | |
| Лист 20 |
40 | 1333,3 | 13,3 | - |
| Уголок 12,5/8 | 14,1 | 73,7 | 22,7 | 74,58 |
| Швейлер 20а | 25,2 | 139 | 1670 | - |
Решение
1. Найдем положение центра тяжести:
Sx =A1 *y1 + A2 *y2 + A3 *y3 =10*40+21,8*14,1+17,72*25,2=1153,924 см3
Sy = A1 *x1 + A2 *x2 + A3 *x3 =1*40+8,49*14,1+12*25,2=462,109 см3
Xc
=![]() =5,8 см
=5,8 см
Yc
=![]() =14,55 см
=14,55 см
2. Вычислим значения осевых и центробежных моментов инерции относительно центральных осей:
IXc
=![]() IXi
+Ai
*ai
2
)=73,7+1333,3+139+4,55*40+3,172
*25,2+7,252
*14,1=3368,46 см4
IXi
+Ai
*ai
2
)=73,7+1333,3+139+4,55*40+3,172
*25,2+7,252
*14,1=3368,46 см4
IYc
=![]() IYi
+Ai
*bi
2
)=13,3+227+1670+4,82
*40+2,692
*14,1+6,22
*25,2=3902,62 см4
IYi
+Ai
*bi
2
)=13,3+227+1670+4,82
*40+2,692
*14,1+6,22
*25,2=3902,62 см4
DXcYc
=![]() DXiYi
+Ai
*ai
*bi
)=0+(-4,55)*(-4,8)*40+74,58+7,25*2,69*14,1+3,17*6,2*25,2=1724,34 см4
DXiYi
+Ai
*ai
*bi
)=0+(-4,55)*(-4,8)*40+74,58+7,25*2,69*14,1+3,17*6,2*25,2=1724,34 см4
3. Определим положение главных центральных осей инерции:
tg2α0
=![]() =6,456
=6,456 ![]() 2α0
=81
2α0
=81![]() 12,
=> α0
=40
12,
=> α0
=40![]() 36,
36,
4. Вычислим значения главных центральных моментов инерции:
Imax/main
=![]()
Imax
=![]() +
+ ==5380,44 см4
==5380,44 см4
Imin
=![]() =
=![]() =1890,64 см4
=1890,64 см4
4. Определим положение главных центральных осей через моменты инерции Imax и Imin :
tgα1
=![]() -1,167
-1,167
α1
=-49![]() 24,
24,
tgα2
=![]() 0,857
0,857
α2
=40![]() 36,
36,
5. Построим круг инерции и по нему проверим положение главных центральных осей и значения главных центральных моментов инерции:

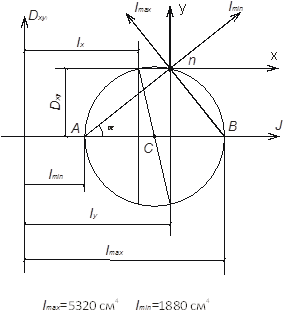
Задача 1.3. Изгиб балок
Проверка прочности балок при изгибе и исследование их деформации
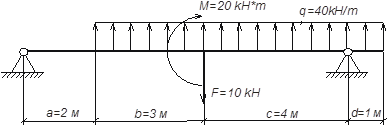
Исходные данные:
| a, м | b, м | c, м | d, м | F, kH | q, kH/м | M, kH*м |
| 2 | 3 | 4 | 1 | 10 | 40 | 20 |
Требуется:
1) построить эпюры поперечных сил и изгибающих моментов
2) подобрать сечение балки двутаврового профиля и проверить прочность принятого сечения по нормальным напряжениям с учетом собственного веса балки
3) вычислить наибольшее касательное напряжение в сечении с максимальным значением поперечной силы
4) в одном из сечений балки, где имеют Q и M большие значения, определить главные напряжения на уровне примыкания полки к стенке и проверить прочность материала по энергетической теории прочности
5) построить эпюры нормальных, касательных, главных и максимальных касательных напряжений в сечении, указанном в п. 4
6) определить аналитическим путем прогибы посередине пролета и на конце консоли и углы поворота сечений на опорах
7) с учетом вычисленных значений прогибов показать на схеме балки очертание ее изогнутой оси
8) проверить жесткость балки при допускаемом значении прогиба v=l/500 и модуле упругости E=2*105 Мпа
1) Определяем опорные реакции.
– Ra *9+q*7*3,5+M-F*4-q*0,5=0
Ra
=![]() =104,4 kH
=104,4 kH
– Rb *9-F*5-M+q*8*6=0
Rb
=![]() =205,6 kH
=205,6 kH
Строим эпюры поперечных сил и изгибающих моментов.
1. Q1 =-Ra =-104,4 kH
2. Q2 =-Ra +q (z-2)=-104,4+120=-15,6 kH
3. Q3 =-Ra +q (z-2) – F=104,4–10+40*7=165,6 kH
4. M1 =-Ra *z=-104,4*2=-108,8 kH/m
5. M2
=-Ra
*z+![]() z=5 -104,4*5+20*32
=342 kH/m
z=5 -104,4*5+20*32
=342 kH/m
z=6 -104,4*4+20*4=337,6 kH/m
z=7 -104,4*3+20=293,2 kH/m

2) Построим сечение балки двутаврового профиля и проверим прочность принятого сечения по нормальным напряжениям с учетом собственного веса.
Wx
![]() =1,6285*10-3
м3
=1628,5 см3
=1,6285*10-3
м3
=1628,5 см3
Подбираем двутавр:
№60
Ix =75450 см4
Wx = 2510 см3
Sx =1450 см3
m=104 кг
Находим опорные реакции с учетом собственного веса.
– Ra *9+q*7*3,5-F*4+M-q*0,5-q1 *9,45+q1 *0,5=0
Ra
=![]() =99,8 kH
=99,8 kH
– Rb *9-F*5-M+q*8*6-q1 *10*5=0
Rb
=![]() =199,8 kH
=199,8 kH
Строим эпюры Q и M с учетом собственного веса.
Q1 =-Ra -q1 *z=-99,8–1,04*2=-101,88 kH
Q2 =-Ra -q1 *z+q*(z-2)=-99,8–5,2+40,3=15 kH
Q3 =-Ra -q1 *z+q*(z-2) – F=-99,8–9,36+280–10=160,84 kH
M1
=-Ra
*z-![]() =-99,8*2–1,04*2=-201,68 kH/m
=-99,8*2–1,04*2=-201,68 kH/m
M2
= Ra
*z-![]() =-332 kH/m
=-332 kH/m

Проверим на прочность.
![]()
![]()
Недонапряжение составляет 30%
3) Вычислим наибольшее касательное напряжение в сечении с максимальным значением поперечной силы
![]() =28,67 МПа
=28,67 МПа
4) В сечении балки, где Q и M имеют большее значение, определяем главное напряжение на уровне примыкания балки к стенке и проверяем прочность материала по энергетической теории прочности
M=208,8 kH/m
Q=104,4 kH
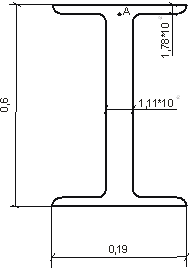
Определяем нормальные напряжения.
![]() =78,1 МПа
=78,1 МПа
Определяем касательные напряжения.
![]() =12,3 МПа
=12,3 МПа
Определяем главные напряжения.
![]() 39,05±40,94
39,05±40,94
![]()
Проверяем прочность материала по энергетической теории.
![]()
![]() 80,9 МПа
80,9 МПа
![]() 80,9 МПа ≤
80,9 МПа ≤![]() =140 МПа
=140 МПа
5) Строим эпюры нормальных, касательных, главных и максимальных касательных напряжений.
Определяем нормальные напряжения
![]() =83 МПа
=83 МПа
![]() =78,1 МПа
=78,1 МПа
![]()
Определяем касательные напряжения.
![]() -0,78 МПа
-0,78 МПа
![]() -12,3 МПа
-12,3 МПа
![]() -18 МПа
-18 МПа
Определяем главные напряжения.
![]()
![]()
![]()
![]()
![]()
![]() -1,89 МПа
-1,89 МПа
![]() 18 МПа
18 МПа
![]() -18 МПа
-18 МПа
Определяем максимальное касательное напряжение
![]() =
=![]() 41,5 МПа
41,5 МПа
![]()
![]() 40,94 МПа
40,94 МПа
![]() 39,05 МПа
39,05 МПа
Строим эпюры.

6) Определяем аналитическим путем прогибы посередине пролета и на конце консоли и углы поворота сечений на опорах.
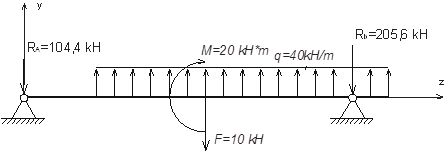
Уравнение углов поворота сечений.
![]()
Уравнение прогибов.
![]()
Находим начальные параметры:
При z=9, ![]() =0
=0
![]() 959 kH
959 kH
Значение прогиба по середине пролета:
При z=4,5
![]()
![]() ср
=
ср
= ![]()
Значение прогиба на конце консоли.
![]()
![]() =-
=- ![]()
Угол поворота на опоре A.
![]()
Угол поворота на опоре B.
![]()
![]()
7) C учетом вычисленных значений прогибов, покажем на схеме балки очертания её изогнутой оси.

8) Проверим жесткость балки при допускаемом значении прогиба
![]() =
=
![]() и модуля упругости
E
=2*105
МПа
и модуля упругости
E
=2*105
МПа
![]()
![]()
Условие по жесткости выполнено.
Похожие работы
-
Задача по теории упругости
Задача №1 Использование плоского напряженного состояния балки-стенки с использованием степенных полиномов Рисунок 1. Решение: Выделим из пластины бесконечно малый элемент
-
Методические рекомендации по выполнению расчетно-графических работ по сопротивлению материалов
Министерство образования Российской Федерации Курский государственный технический университет Кафедра сопротивления материалов и строительной механики
-
Расчет балки на жесткость
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра сопротивления материалов
-
Геология, основания и фундаменты
Геология, основания и фундаменты 4.1. Основные положения по расчету и проектированию свайных фундаментов Фундаменты из забивных свай рассчитываются в соответствии с требованиями СНиП 2.02.03-85 по двум предельным состояниям:
-
Расчет фундамента здания
Расчет свайных фундаментов из забивных призматических свай на грунтах II типа по просадочности. Определение типа грунтовых условий и их удельного веса в водонасыщенном состоянии. Расчет просадки фундамента, выбор длины свай и вычисление нагрузки на них.
-
Испытание стержней на устойчивость
Определение критической силы для центрального сжатого стержня и пределов применения расчетных формул. Предельная гибкость. Фактическая гибкость для двух типов закрепления концов стержня. Критическая сила для двух типов закрепления концов стержня.
-
Основы расчетов прочностной надежности элементов конструкций
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ МЕЖДУНАРОДНЫЙ ИНСТИТУТ КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ ЛИПЕЦКИЙ ФИЛИАЛ Кафедра "СГ и ОПД"
-
Конструкции городских зданий и сооружений
Конструктивное решение промышленного здания. Расчет стропильной фермы, критерии ее выбора, сбор нагрузок и статический расчет. Подбор сечений стержней фермы. Конструирование и расчет узлов ферм. Расчетные характеристики сварного углового шва металла.
-
Расчет статически неопределимой рамы методом сил
Составление эквивалентной схемы рамы. Порядок составления канонического уравнения. Получение эпюры изгибающих моментов. Производство расчета поперечных сил действующих в раме и расчет продольных сил действующих в раме. Получение эпюры продольных сил.
-
Построение эпюр внутренних силовых факторов
Анализ характера распределения внутренних сил упругости при помощи метода сечений. Виды сопротивлений: растяжение (сжатие), кручение, чистый изгиб. Опорные закрепления – понятие и разновидности. Построение эпюр продольных сил и крутящих моментов.