Название: Общие характеристики пакета Control System Toolbox

Вид работы: реферат

Рубрика: Информатика

Размер файла: 223.08 Kb

Скачать файл: referat.me-132994.docx

Краткое описание работы: (CST) Исследование систем автоматического управления начинаются с создания математической модели. В пакете CST линейные модели могут быть представлены в четырех формах:

Общие характеристики пакета Control System Toolbox

Общие характеристики пакета ControlSystemToolbox(CST)

Исследование систем автоматического управления начинаются с создания математической модели. В пакете CST линейные модели могут быть представлены в четырех формах:

· передаточная ф-ция(tf)

· нули, полюса и коэффициент усиления(zpk)

· пространство состояния(ss)

· частотные характеристики(frd)

Програма№1

>> h1=tf([1,0],[1,2,10])

Transfer function:

s

--------------

s^2 + 2 s + 10

>> z=0

z =

0

>> p=[2,1+j,1-j]

p =

2.0000 1.0000 + 1.0000i 1.0000 - 1.0000i

>> k=2

k =

2

>> H=zpk(z,p,k)

Zero/pole/gain:

2 s

--------------------

(s-2) (s^2 - 2s + 2)

>> A=[0,1;-5,-2]

A =

0 1

-5 -2

>> B=[0;3]

B = 0

3

>> C=[1,0]

C =

1 0

>> D=0

D =

0

>> H1=ss(A,B,C,D)

a =

x1 x2

x1 0 1

x2 -5 -2

b =

u1

x1 0

x2 3

c =

x1 x2

y1 1 0

d =

u1

y1 0

Continuous-time model.

>> h2=tf([2,0],[5,1])

Transfer function:

2 s

-------

5 s + 1

>> fred=[1,2,5,10,20]

fred =

1 2 5 10 20

>> H2=frd(h2,fred)

Frequency(rad/s) Response

---------------- --------

1 0.3846 + 0.0769i

2 0.3960 + 0.0396i

5 0.3994 + 0.0160i

10 0.3998 + 0.0080i

20 0.4000 + 0.0040i

Continuous-time frequency response.

>> figure(1)

>> bode(H2),grid on

>> h11=ss(A,B,C,D)

a =

x1 x2

x1 0 1

x2 -5 -2

b =

u1

x1 0

x2 3

c =

x1 x2

y1 1 0

d =

u1

y1 0

Continuous-time model.

>> h22=tf(h11)

Transfer function:

3

-------------

s^2 + 2 s + 5

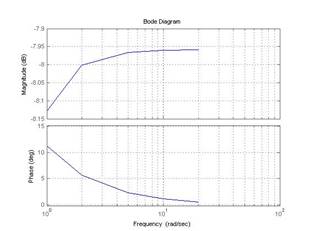
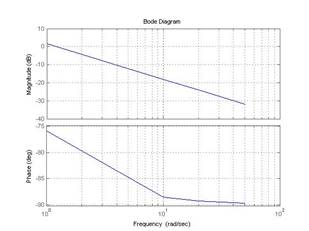
В пакете CST имеются команды, позволяющие получать математическое описание сложных систем по их структурным схемам.

Програма№2

>> h1=tf([4],[5,1])

Transfer function:

4

-------

5 s + 1

>> h2=tf([1,0],[1,2,10])

Transfer function:

s

--------------

s^2 + 2 s + 10

>> H=series(h1,h2)

Transfer function:

4 s

--------------------------

5 s^3 + 11 s^2 + 52 s + 10

>> H1=h1*h2

Transfer function:

4 s

--------------------------

5 s^3 + 11 s^2 + 52 s + 10

>> H2=parallel(h1,h2)

Transfer function:

9 s^2 + 9 s + 40

--------------------------

5 s^3 + 11 s^2 + 52 s + 10

>> H20=h1+h2

Transfer function:

9 s^2 + 9 s + 40

--------------------------

5 s^3 + 11 s^2 + 52 s + 10

>> H3=feedback(h1,h2)

Transfer function:

4 s^2 + 8 s + 40

--------------------------

5 s^3 + 11 s^2 + 56 s + 10

>> H4=feedback(h1,h2,+1)

Transfer function:

4 s^2 + 8 s + 40

--------------------------

5 s^3 + 11 s^2 + 48 s + 10

>> H5=[h1,h2]

Transfer function from input 1 to output:

4

-------

5 s + 1

Transfer function from input 2 to output:

s

--------------

s^2 + 2 s + 10

>> H6=[h1;h2]

Transfer function from input to output...

4

#1: -------

5 s + 1

s

#2: --------------

s^2 + 2 s + 10

>> H7=append(h1,h2)

Transfer function from input 1 to output...

4

#1: -------

5 s + 1

#2: 0

Transfer function from input 2 to output...

#1: 0

s

#2: --------------

s^2 + 2 s + 10

Вариант№1

K1	10
K2	5
K3	12
K4	6
T1	8
T3	4
T4	2
T5	1
T6	3
T7	5

Структурная схема

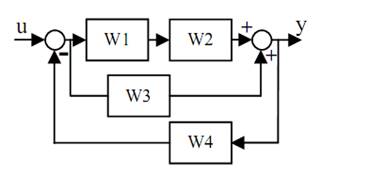
Таблица значений функций

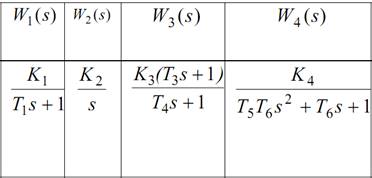
Програма№3

>> variant=1;

>> W1=tf([10],[8,1])

Transfer function:

10

-------

8 s + 1

>> W2=tf([5],[1,0])

Transfer function:

5

-

s

>> W3=tf([12*4,12],[2,1])

Transfer function:

48 s + 12

---------

2 s + 1

>> W4=tf([6],[1*3,3,1])

Transfer function:

6

---------------

3 s^2 + 3 s + 1

>> H1=W1*W2

Transfer function:

50

---------

8 s^2 + s

>> H2=H1+W3

Transfer function:

384 s^3 + 144 s^2 + 112 s + 50

------------------------------

16 s^3 + 10 s^2 + s

>> Q=feedback(H2,W4)

Transfer function:

1152 s^5 + 1584 s^4 + 1152 s^3 + 630 s^2 + 262 s + 50

-----------------------------------------------------

48 s^5 + 78 s^4 + 2353 s^3 + 877 s^2 + 673 s + 300

h=tf([1152,1584,1152,630,262,50],[48,78,2353,877,673,300])

Transfer function:

1152 s^5 + 1584 s^4 + 1152 s^3 + 630 s^2 + 262 s + 50

-----------------------------------------------------

48 s^5 + 78 s^4 + 2353 s^3 + 877 s^2 + 673 s + 300

>> figure(1)

>> step(h),grid on

>> figure(2)

>> impulse(h),grid on

>> figure(3)

>> bode(h),grid on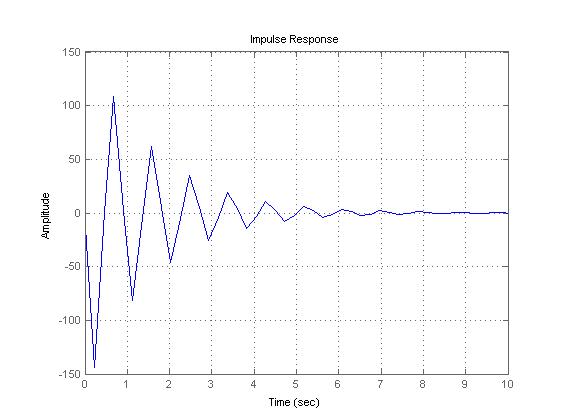

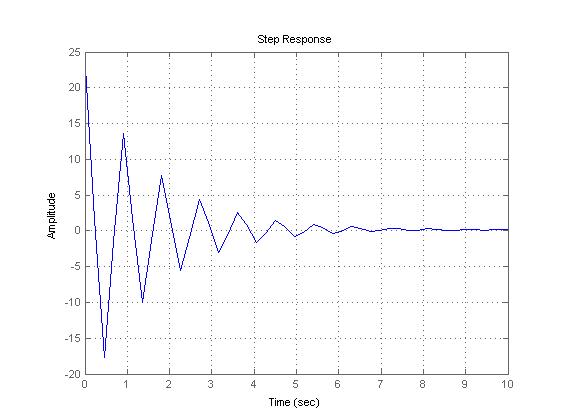
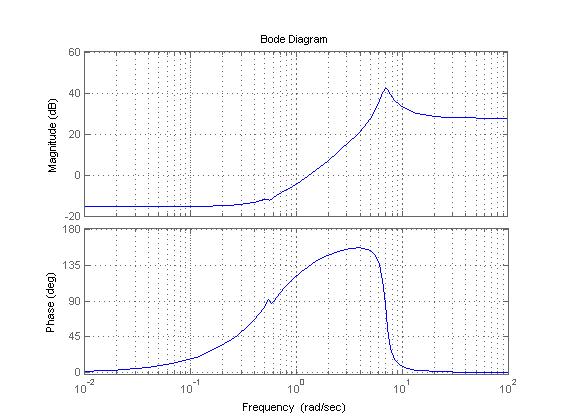
Вывод. Изучили возможности MatLab по созданию и преобразованию моделей линейных систем. Создали и преобразовали модели линейных систем, определили реакции типовых звеньев на гармонические воздействия.