Название: Кривые второго порядка. Квадратичные формы

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 38.58 Kb

Скачать файл: referat.me-214622.docx

Краткое описание работы: Понятие квадратичной формы и способы ее записи. Действительные и недействительные, вырожденные и невырожденные формы, ранг матрицы. Знакоопределенность квадратичных форм, определение ее миноров. Критерии положительной и отрицательной определенностей.

Кривые второго порядка. Квадратичные формы

Высшая математика

Кривые второго порядка

Квадратичные формы

Содержание

1. Понятие квадратичной формы и способы ее записи

2. Знакоопределенность квадратичных форм

3. Критерии положительной и отрицательной определенностей

Литература

1. Понятие квадратичной формы и способы ее записи

Квадратичной формой j (х₁ , х₂ , …, x_n ) n действительных переменных х₁ , х₂ , …, x_n называется сумма вида

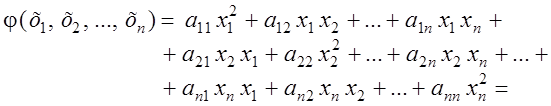
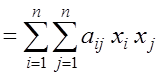,(1)

где a_ij – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что a_ij = a_ji .

Квадратичная форма называется действительной, если a_ij Î ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица

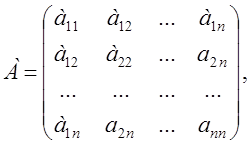
то есть А^Т = А. Следовательно, квадратичная форма (1) может быть записана в матричном виде j(х) = х^Т Ах, где

х^Т = (х₁ х₂ … x_n ). (2)

И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А. (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.

Пример 1.

Записать матрицу квадратичной формы

j (х₁ , х₂ , x₃ ) = – 6х₁ х₂ – 8х₁ х₃ + + 4х₂ х₃ –

и найти ее ранг.

Решение.

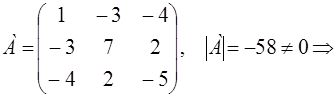
Þr(A) = 3 Þ

квадратичная форма невырождена.

2. Знакоопределенность квадратичных форм

Квадратичная форма (1) называется положительно определенной (или строго положительной), если j(х) > 0, для любого х = (х₁ , х₂ , …, x_n ), кроме х = (0, 0, …, 0).

Матрица А положительно определенной квадратичной формы j(х) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.

Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если j(х) < 0, для любого х = (х₁ , х₂ , …, x_n ), кроме х = (0, 0, …, 0).

Аналогично как и выше, матрица отрицательно определенной квадратичной формы также называется отрицательно определенной.

Следовательно, положительно (отрицательно) определенная квадратичная форма j(х) достигает минимального (максимального) значения j(х*) = 0 при х* = (0, 0, …, 0).

Отметим, что большая часть квадратичных форм не является знакоопределенными, то есть они не являются ни положительными, ни отрицательными. Такие квадратичные формы обращаются в 0 не только в начале системы координат, но и в других точках.

Пример 2.

Определить знакоопределенность следующих квадратичных форм.

1)

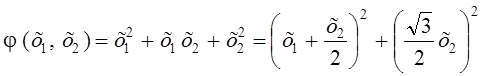
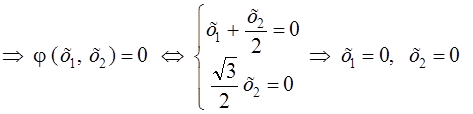
Þ

т. е. квадратичная форма является положительно определенной.

2)

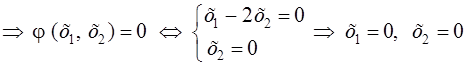
Þ

т. е. квадратичная форма является отрицательно определенной.

3)

Þ

данная квадратичная форма не является знакоопределенной, так как она равна 0 во всех точках прямой х₁ = –х₂ , а не только в начале системы координат.

Когда n > 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.

Главными минорами квадратичной формы называются миноры:

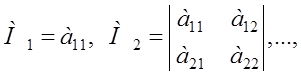
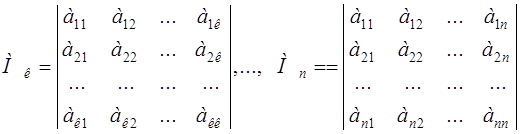
то есть это миноры порядка 1, 2, …, n матрицы А, расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А.

3. Критерий положительной и отрицательной определенности

Критерий положительной определенности (критерий Сильвестра)

Для того чтобы квадратичная форма j(х) = х^Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть:

М₁ > 0, M₂ > 0, …, M_n > 0.

Критерий отрицательной определенности

Для того чтобы квадратичная форма j(х) = х^Т Ах была отрицательно определенной, необходимо и достаточно, чтобы ее главные миноры четного порядка были положительны, а нечетного – отрицательны, то есть:

М₁ < 0, M₂ > 0, М₃ < 0, …, (–1)ⁿ M_n > 0.

Пример 3.

При каких значениях а и в квадратичная форма будет положительно определенной?

j (х₁ , х₂ , x₃ ) =

Решение.

Построим матрицу А и найдем ее главные миноры.

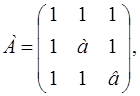М₁ = 1 > 0,

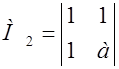= а – 1 > 0 Þ а > 1.

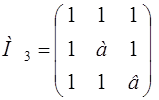= ав – а – в > 0 Þв > .

Ответ:

а > 1, в > .

Пример 4.

При каких значениях а и в квадратичная форма будет отрицательно определенной?

j (х₁ , х₂ , x₃ ) =

Решение.

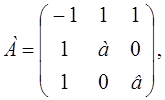М₁ = –1 < 0,

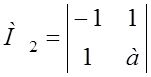= –а – 1 > 0 Þ а < –1.

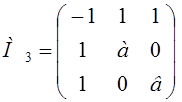= –ав – а – в < 0 Þв > – .

Ответ

а < –1, в > –.

Пример 5.

Доказать, что квадратичная форма

j (х₁ , х₂ , x₃ ) =

положительно определена.

Решение.

Воспользуемся критерием Сильвестра. Построим матрицу А и найдем главные миноры матрицы А.

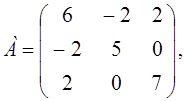
М₁ = 6 > 0, 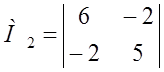= 26 > 0, М₃ = ú А ç = 162 > 0

Þj (х₁ , х₂ , x₃ )

положительно определенная квадратичная форма.

Литература

1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.

2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.