Название: Вычисление случайных величин

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 190.6 Kb

Скачать файл: referat.me-214757.docx

Краткое описание работы: Задача №1. Двумерная случайная величина (X,Y) имеет равномерное распределение вероятностей в треугольной области ABC: где S – площадь треугольника ABC.

Вычисление случайных величин

Задача №1.

Двумерная случайная величина (X,Y) имеет равномерное распределение вероятностей в треугольной области ABC:

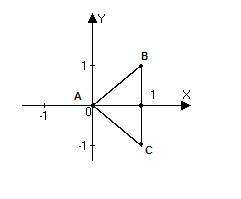
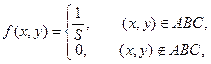
где S – площадь треугольника ABC.

Определить плотности случайных величин X и Y, математические ожидания M(X) и M(Y), дисперсии D(X) и D(Y), а также коэффициент корреляции . Являются ли случайные величины X и Y независимыми?

Решение.

Разделим область ABC на две равные части вдоль оси OX, тогда из условия

или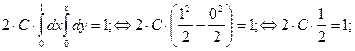

следует, что

Тогда плотность двумерной случайной величины (X,Y):

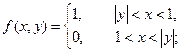
Вычислим плотность составляющей X:

при ,

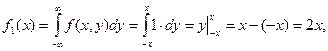
откуда плотность составляющей X–

Вычислим плотность составляющей Y:

при ,

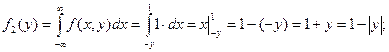
при ,

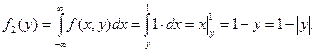
Поэтому плотность составляющей Y –

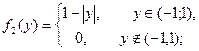
Найдем условную плотность составляющей X:

при , случайные величины X и Y зависимы.

Найдем математическое ожидание случайной величины X:

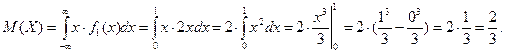
Найдем дисперсию случайной величины X:

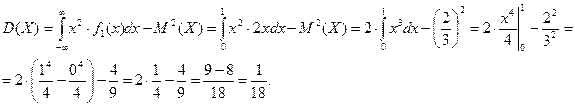
Найдем среднеквадратическое отклонение случайной величины X:

Найдем математическое ожидание случайной величины Y:

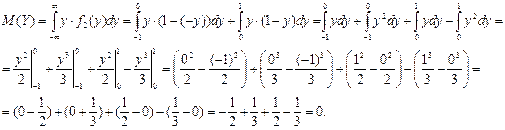
Найдем дисперсию случайной величины Y:

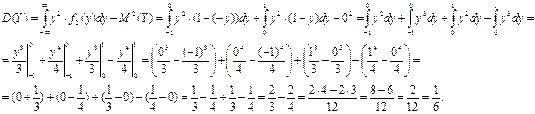
Найдем среднеквадратическое отклонение случайной величины Y:

Найдем математическое ожидание двумерной случайной величины (X,Y):

Тогда ковариация: ,

а значит и коэффициент корреляции

Следовательно, случайные величины X и Y - зависимые, но некоррелированные.

Задача №2

Двумерная случайная величина (X,Y) имеет следующее распределение вероятностей:

Y	X
	3	6	8	9
-0,2	0,035	0,029	0,048	0,049
0,1	0,083	0,107	0,093	0,106
0,3	0,095	0,118	0,129	0,108

Найти коэффициент корреляции между составляющими X и Y.

Решение.

Таблица распределения вероятностей одномерной случайной величины X:

X	3	6	8	9
	0,213	0,254	0,270	0,263

Проверка: + + + = 0,213 + 0,254 + 0,270 + 0,263 = 1.

Таблица распределения вероятностей одномерной случайной величины Y:

Y	-0,2	0,1	0,3
	0,161	0,389	0,450

Проверка: + + = 0,161 + 0,389 + 0,450 = 1.

Вычислим числовые характеристики случайных величин X и Y.

1. Математическое ожидание случайной величины X:

2.

Математическое ожидание случайной величины Y:

3. Дисперсия случайной величины X:

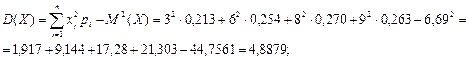
4. Дисперсия случайной величины Y:

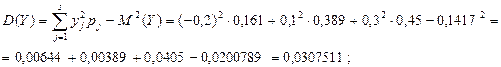
5. Среднеквадратическое отклонение случайной величины X:

6. Среднеквадратическое отклонение случайной величины Y:

Таблица распределения вероятностей случайной величины X-M(X):

X-M(X)	3-M(X)	6-M(X)	8-M(X)	9-M(X)
	0,213	0,254	0,270	0,263

Таблица распределения вероятностей случайной величины Y-M(Y):

Y-M(Y)	-0,2-M(Y)	0,1-M(Y)	0,3-M(Y)
	0,161	0,389	0,450

Таблица распределения вероятностей случайной величины [X-M(X)][Y-M(Y)]:

[X-M(X)][Y-M(Y)]	1,260873	0,153873
P	0,035	0,083

-0,584127	0,235773	0,028773	-0,109227	-0,447627
0,095	0,029	0,107	0,118	0,048

-0,054627	0,207373	-0,789327	-0,096327	0,365673
0,093	0,129	0,049	0,106	0,108

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

Найдем ковариацию:

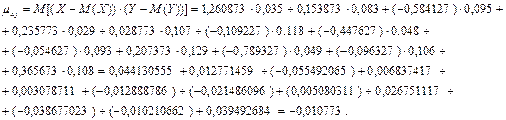
Найдем коэффициент корреляции:

Ответ: -0,028.

Задача №3

Рост, см (X)		Вес, кг (Y)
		22,5-25,5	25,5-28,5	28,5-31,5	31,5-34,5	34,5-37,5
117,5-122,5		1	3	-	-	-
122,5-127,5		-	2	6	1	-
127,5-132,5		-	1	5	5	-
132,5-137,5		-	1	6	7	2
137,5-142,5		-	-	1	4	2
142,5-147,5		-	-	-	1	1
147,5-152,5	-		-	-	-	1

Результаты обследования 50 учеников:

По данным таблицы требуется:

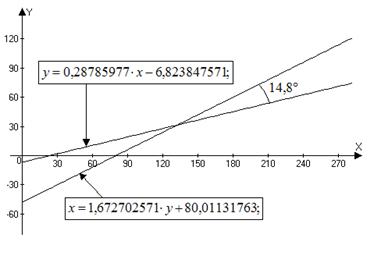
- написать выборочные уравнения прямых регрессии Y на X и X на Y;

- вычертить их графики и определить угол между ними;

- по величине угла между прямыми регрессии сделать заключение о величине связи между X и Y.

Решение.

Принимая рост всех учеников, попавших в данный интервал, равным середине этого интервала, а вес – равным середине соответствующего интервала, получим так называемую корреляционную таблицу:

Для роста X получим:

1. Выборочная средняя –

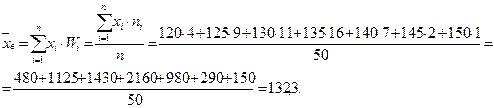
2. Дисперсия выборочная исправленная –

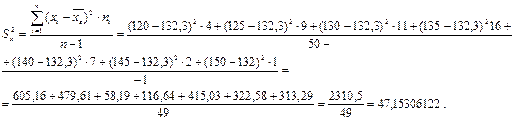
Для веса Y получим:

1. Выборочная средняя -

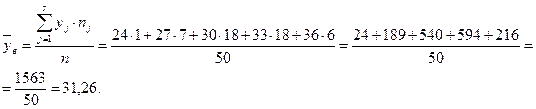
2. Дисперсия выборочная исправленная –

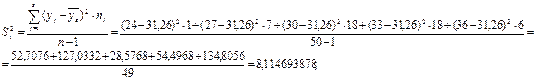
Найдем выборочный коэффициент корреляции:

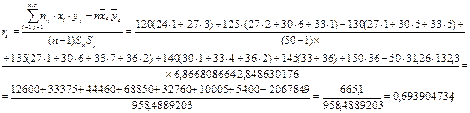
Найдем значения коэффициентов регрессии:

Уравнение прямой регрессии Y на X имеет вид:

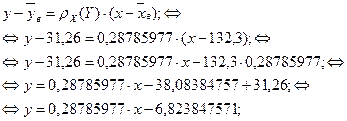
Уравнение прямой регрессии X на Y имеет вид:

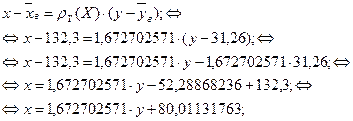
- угол между прямыми регрессии.

Следовательно, связь между X и Y не тесная.