Название: Ряд распределения функция распределения
Вид работы: лабораторная работа
Рубрика: Математика
Размер файла: 85.6 Kb
Скачать файл: referat.me-218230.docx
Краткое описание работы: Задача 1 (5) Производится контроль партии из 4 изделий. Вероятность изделия быть неисправным равна 0,1. Контроль прекращается при обнаружении первого неисправного изделия. Х – число обследованных приборов. Найти:а) ряд распределения Х б)функцию распределения F(X), в ответ ввести F(3.5). в) m(x) г) d(x) д) p(1.5<X<3.5).
Ряд распределения функция распределения
Задача 1 (5)
Производится контроль партии из 4 изделий. Вероятность изделия быть неисправным равна 0,1. Контроль прекращается при обнаружении первого неисправного изделия. Х – число обследованных приборов. Найти:а) ряд распределения Х б)функцию распределения F(X), в ответ ввести F(3.5). в) m(x) г) d(x) д) p(1.5<X<3.5).
Решение
Пусть событие А – состоит в том, что изделие исправно, и соответственно 
- неисправно. По условию, вероятность 
, значит p(A)=1-
. Случайная величина Х – число обследованных приборов – может принимать значения 0(если первый же прибор неисправен),1,2,3,4.
Найдем соответствующие вероятности:
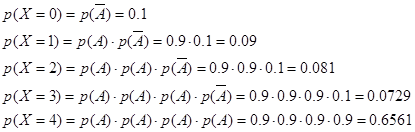
Составим ряд распределения Х:
| Х | 0 | 1 | 2 | 3 | 4 |
| р | 0,1 | 0,09 | 0,081 | 0,0729 | 0,6561 |
Х – дискретная случайная величина. Найдем функцию распределения F(x)=P(X
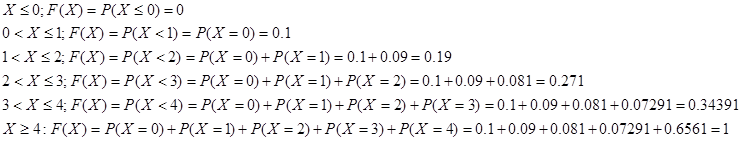
Значение F(3.5)=0.34391
Математическое ожидание дискретной случайной величины 
Дисперсия 
Вероятность 
Задача 2(2 ). События А и В независимы. Вероятность наступления хотя бы одного из них равна 0,94. Найти Р(А), если Р(В)=0,7. Ответ записать в виде десятичной дроби.
Решение.
Вероятность наступления суммы событий Р(А+В)=Р(А)+Р(В)-Р(АВ). Но так как события А и В независимы, то Р(АВ)=Р(А)Р(В).
Имеем Р(А+В)=0,94 (наступает событие А или событие В или оба); Р(В)=0,7
0,94=Р(А)+0,7- Р(А)
0,3Р(А)=0,94-0,7=0,24
Р(А)=
- вероятность наступления А.
Задача 3(6). Дана плотность распределения случайной величины Х:
Найти а)константу А б)функцию распределения F(x), в ответ ввести F(0); F(0.5) в) m(x) г)d(x)
д) P(0<X<0.5).
Решение.
Константу А найдем из условия для р(х) :
Имеем 
Отсюда 
.
Функция распределения непрерывной случайной величины 
Для 
p(x)=0, F(x)=0
Для -
Для 
Математическое ожидание непрерывной случайной величины 
Имеем 
Дисперсия непрерывной случайной величины 
Имеем
Вероятность
Задача 4(2). Дана плотность распределения вероятностей системы (X,Y).
Найти а)константу С;б)р1(х),р2(у); в) mx; г)my ;д)Dx; е)Dy; ж)cov(X,Y); з)rxy; и)F(-1,5); к) M(X|Y=1)
Решение. Плотность системы случайных величин должна удовлетворять условию:
В нашем случае 
; 
; 
; 
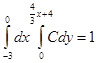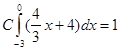Y
B 4
-3 A 0 X
б) Плотности р1(х),р2(у):
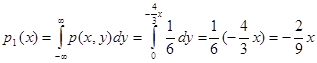
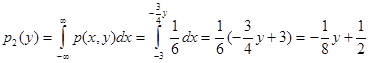
в) Математические ожидания:
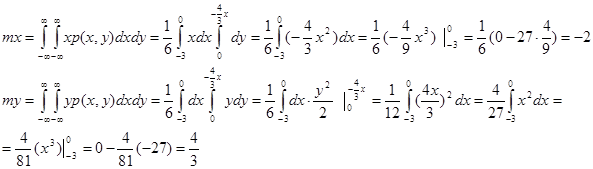
г) Дисперсии:
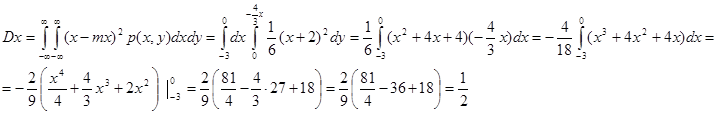
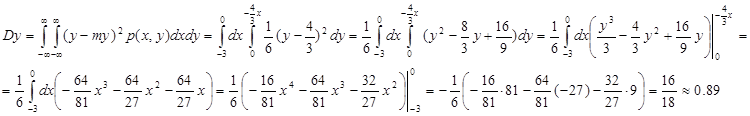ж) Ковариация
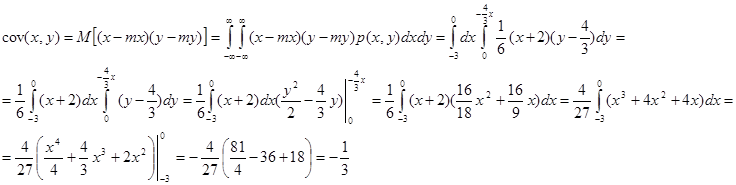з) Коэффициент корреляции
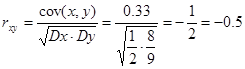
и) Значение F(-1,5)
Функция распределения системы случайных величин
. (1)
(-1,5) Y
5
B
D4 4
D1 D0
A X
-3 -1 O
D2 D3
В областях D1,D2,D3,D4 которые не пересекаются с треугольником АВО значениеP(x,y)=0
Вычисляя F(-1,5) представим двойной интеграл в виде суммы интегралов:
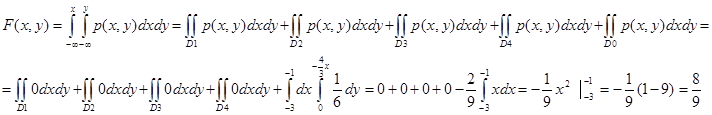
к) Математическое ожидание M(x|y=1)
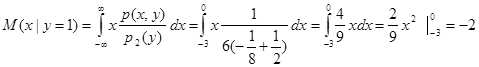
Похожие работы
-
Типовой расчет
Анализ решений заданий по теории вероятности: определить вероятность того, что на верхних гранях двоих костей сумма очков не превосходит 12, определить среди лотерейных билетов вероятное количество выигрышных и количество бракованного товара в партии.
-
Контрольная по теории вероятности
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ Факультет заочного и послевузовского обучения КОНТРОЛЬНАЯ РАБОТА №1
-
Вычисления по теории вероятностей
Применение классического определения вероятности в решении экономических задач. Определение вероятности попадания на сборку бракованных и небракованных деталей. Вычисление вероятности и выборочного значения статистики при помощи формулы Бернулли.
-
Теория вероятностей
Поиск искомой вероятности через противоположное событие. Интегральная формула Муавра–Лапласа. Нахождение вероятности попадания в заданный интервал распределенной случайной величины по ее математическому ожиданию и среднему квадратическому отклонению.
-
Теория вероятностей
Характеристика полной группы событий как совокупность всех возможных результатов опыта. Способы определения вероятности событий в задачах разного направления. Нахождение вероятности количества нестандартных деталей. Построение функции распределения.
-
Теория вероятности и математическая статистика
Классическое определение вероятности события. Способы вычисления наступления предполагаемого события. Построение многоугольника распределения. Поиск случайных величин с заданной плотностью распределения. Решение задач, связанных с темой вероятности.
-
Математическая статистика
Исследование сходимости рядов. Степенной ряд интеграла дифференциального уравнения. Определение вероятности событий, закона распределения случайной величины, математического ожидания, эмпирической функции распределения, выборочного уравнения регрессии.
-
Формула Лапласа. Математическое ожидание
Задача на определение вероятности попадания при одном выстреле первым орудием, при условии, что для второго орудия эта вероятность равна 0,75. Интегральная формула Лапласа. Решение задачи на определение математического ожидания случайной величины.
-
Основы теории вероятностей
Закон распределения случайной величины Х, функция распределения и формулы основных числовых характеристик: математическое ожидание, дисперсия и среднеквадратичное отклонение. Построение полигона частот и составление эмпирической функции распределения.
-
Законы распределения случайных величин. Доверительный интервал
Определение вероятности появления события в каждом из независимых испытаний. Случайные величины, заданные функцией распределения (интегральной функцией), нахождение дифференциальной функции (плотности вероятности), математического ожидания и дисперсии.