Название: Интеграл дифференциального уравнения

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 65.5 Kb

Скачать файл: referat.me-215169.docx

Краткое описание работы: Проверка непрерывности заданных функций. Интегрирование заданного уравнения и выполние преобразования с ним. Интегрирование однородного дифференциального уравнения. Решение линейного дифференциального уравнения. Общее решение неоднородного уравнения.

Интеграл дифференциального уравнения

АНО ВПО «НАЦИОНАЛЬНЫЙ ИНСТИТУТ ИМЕНИ ЕКАТЕРИНЫ ВЕЛИКОЙ»

Контрольное задание

По дисциплине: «Математика»

Москва 2010 г.

Контрольное задание:

Упражнения

1. Дана последовательность а_n =(3n-5)/(4n+1). Установить номер n₀ , начиная с которого выполняется неравенство │а_n -А │ < 1/500.

Отв. n₀ =719.

Найти:

2. lim (3-√х)/(х² -81).Отв. –1/108.

х→9

3. lim (5х² -8)/(х³ -3х² +11).Отв. 0.

х→∞

Проверить непрерывность следующих функций:

4. у=5х/(х³ +8).Отв. При всех х≠–2 функция непрерывна.

5. у=(х² +4)/ √(х² -36). Отв. Функция непрерывна при всех значениях

│х│>6.

6. Определить точки разрыва функции у=(8х+2)/(16х² -1).

Отв . Точки х₁ =–1/4 и х₂ =1/4.

Задача 1

Найти общий интеграл дифференциального уравнения:

Решение

Выполним разделение переменных, для этого разделим обе части уравнения на :

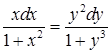
Проинтегрируем обе части уравнения и выполним преобразования:

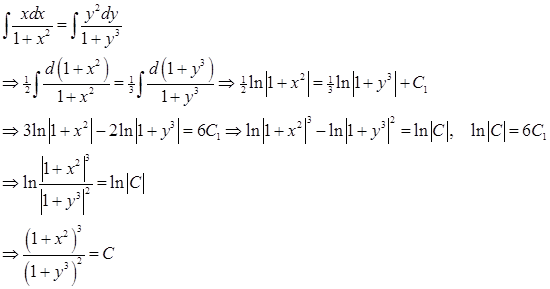
Ответ

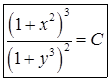
Задача 2

Проинтегрировать однородное дифференциальное уравнение:

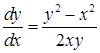
Решение

Решение однородных дифференциальных уравнений осуществляется при помощи подстановки:

,

С учетом этого, исходное уравнение примет вид:

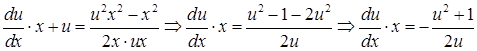
Выполним разделение переменных, для этого умножим обе части уравнения на 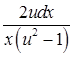, получим,

Проинтегрируем обе части уравнения и выполним преобразования:

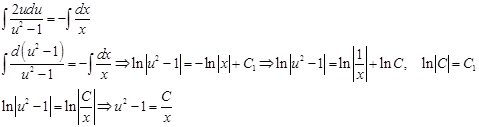
Возвращаясь к переменной y , получим общий интеграл исходного уравнения:

Ответ

Задача 3

Найти общий интеграл дифференциального уравнения:

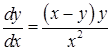
Решение

Покажем, что данное уравнение является однородным, т.е. может быть представлено в виде, . Преобразуем правую часть уравнения:

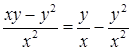
Следовательно, данное уравнение является однородным и для его решения будем использовать подстановку,

С учетом этого, уравнение примет вид:

Выполним разделение переменных, для этого умножим обе части уравнения на ,

Проинтегрируем обе части уравнения,

Возвращаясь к переменной y , получим,

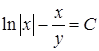
Ответ

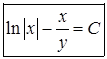
Задача 4

Решить линейное дифференциальное уравнение:

Решение

Составим характеристическое уравнение и найдем его корни:

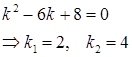
Так как корни характеристического уравнения действительные и различны, то решение дифференциального уравнения будет иметь вид:

Ответ

Задача 5

Найти общее решение дифференциального уравнения:

Решение

Общее решение неоднородного уравнения будем искать в виде:

,

где – частное решение исходного неоднородного ДУ, – общее решение соответствующего однородного уравнения:

Составим характеристическое уравнение и найдем его корни:

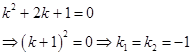
Так как корни характеристического уравнения действительные и совпадают, то общее решение однородного ДУ будет иметь вид:

Учитывая, что правая часть имеет специальный вид, то частное решение неоднородного уравнения будем искать в виде,

,

где A , B , C – неопределенные коэффициенты. Найдем первую и вторую производные по x от и подставим полученные результаты в исходное уравнение:

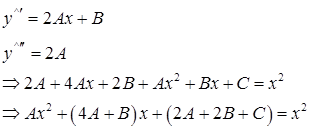
Приравняем коэффициенты при соответствующих степенях x и определим их:

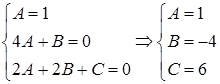
Следовательно, частное решение неоднородного ДУ примет вид:

Окончательно, общее решение исходного ДУ:

Ответ

Задача 6

Решить уравнение:

Решение

Общее решение неоднородного уравнения будем искать в виде:

,

где – частное решение исходного неоднородного ДУ, – общее решение соответствующего однородного уравнения:

Составим характеристическое уравнение и найдем его корни:

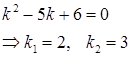
Так как корни характеристического уравнения действительные и различны, то общее решение однородного ДУ будет иметь вид:

Учитывая, что правая часть имеет специальный вид, то частное решение неоднородного уравнения будем искать в виде,

,

где A , B , C – неопределенные коэффициенты. Найдем первую и вторую производные по x от и подставим полученные результаты в исходное уравнение:

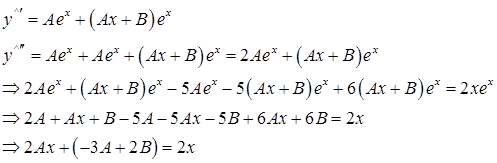
Приравняем коэффициенты при соответствующих степенях x и определим их:

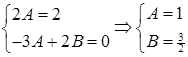
Следовательно, частное решение неоднородного ДУ примет вид:

Окончательно, общее решение исходного ДУ:

Ответ

Комментарии к решению

В задаче №1, опечатка в предполагаемом ответе, упущен показатель степени при x .

В задаче №3, ответ следует оставить в виде, содержащем модуль , т.к. нет достаточных оснований его снять.