Referat.me
/ / Решение дифференциальных уравнений

Название: Решение дифференциальных уравнений

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 87.61 Kb

Скачать файл: referat.me-217631.docx

Краткое описание работы: Задачи на нахождение неопределенного интеграла с применением метода интегрирования по частям. Вычисление площади, ограниченной заданными параболами. Решение дифференциального уравнения первого порядка. Исследование на сходимость ряда; признаки сходимости.

Решение дифференциальных уравнений

Задача 4

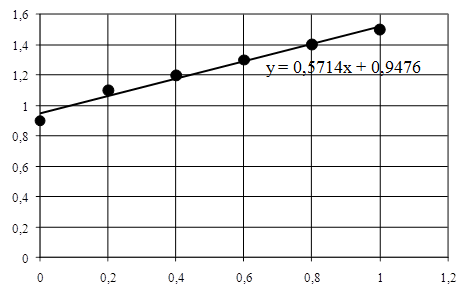
С помощью метода наименьших квадратов подобрать параметры a и b линейной функции y = a + bx , приближенно описывающей опытные данные из соответствующей таблицы. Изобразить в системе координат заданные точки и полученную прямую.

xi 0,0 0,2 0,4 0,6 0,8 1,0
yi 0,9 1,1 1,2 1,3 1,4 1,5

Решение

Система нормальных уравнений

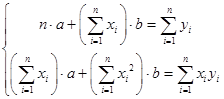
в задаче

n = 6

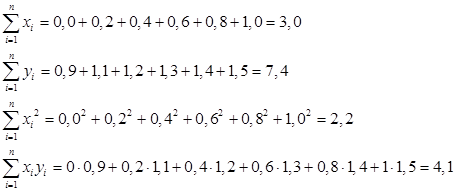
Тогда


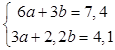
решая ее получаем .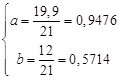

y = 0,5714x + 0,9476

Задача 5

Найти неопределенный интеграл

Решение


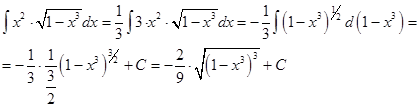
Ответ:

Задача 6

Найти неопределенный интеграл

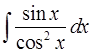
Решение

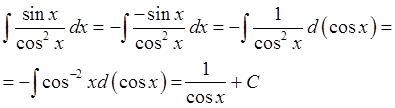
Ответ: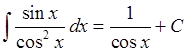

Задача 7

Найти неопределенный интеграл, применяя метод интегрирования по частям

Решение


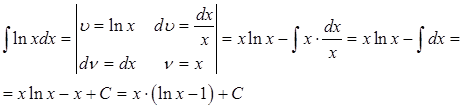
Ответ:

Задача 8

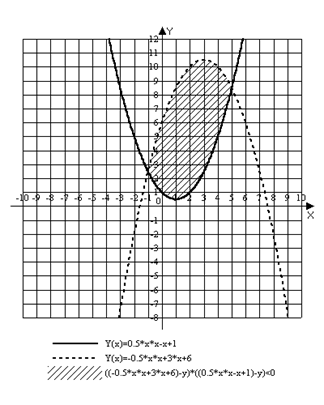
Вычислить площадь, ограниченную заданными параболами

Решение

Точки пересечения по х: х = -1, х = 5.

Площадь фигуры найдем из выражения

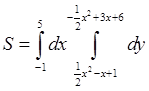
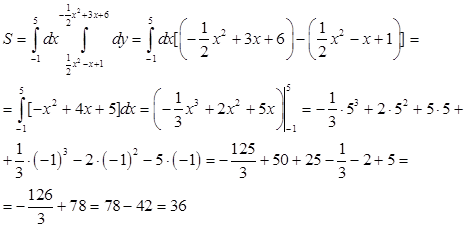
Ответ:

Задача 9

Найти общее решение дифференциального уравнения первого порядка

Решение

Разделим переменные

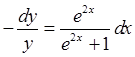
Проинтегрируем

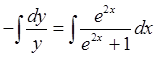
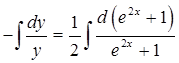
Ответ:

Задача 10

Найти частное решение линейного дифференциального уравнения первого порядка, удовлетворяющее начальному условию

Решение:

Запишем функцию y в виде произведения y = u * v. Тогда находим производную:

Подставим эти выражения в уравнение


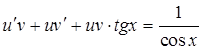
Выберем v таким, чтобы

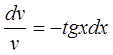
Проинтегрируем выражение

,

Найдем u

,

,

,

,

Тогда

Тогда

Ответ:

Задача 11

Исследовать на сходимость ряд:

а) с помощью признака Даламбера знакоположительный ряд

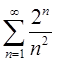
Решение

Проверим необходимый признак сходимости ряда

n®¥
n®¥
n®¥
Т. к. , то необходимый признак сходимости ряда не соблюдается, и ряд расходится.

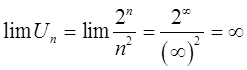
Используем признак Даламбера

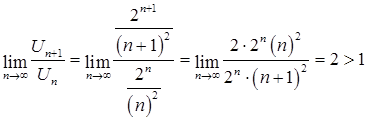
Ответ: ряд расходится


б) с помощью признака Лейбница знакочередующийся ряд

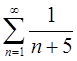
Решение

Проверим необходимый признак сходимости ряда

n®¥
n®¥
n®¥
Т. к. , то необходимый признак сходимости ряда соблюдается, можно исследовать ряд на сходимость.

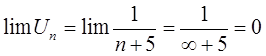
По признаку подобия

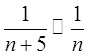
данный ряд аналогичен гармоническому ряду начиная с пятого члена, таким образом, т.к. гармонический ряд расходится, то и исходный ряд расходится.

Ответ: ряд расходится

в) Найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости


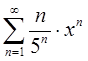
Решение

Используем признак Даламбера:

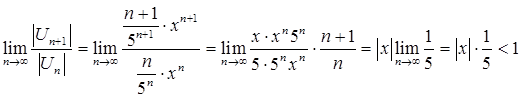
При х =5 получим ряд

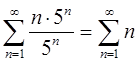
Ряд знакопостоянный, limUn = n

Ряд расходится, так как состоит из суммы возрастающих элементов, каждый из которых больше 1.

При х = -5 получим ряд

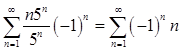
Ряд знакочередующийся, limUn = n

|Un | > |Un +1 | > |Un +2 | … - не выполняется.

По теореме Лейбница данный ряд расходится

Ответ: Х Î(-5; 5)


Задача 12

Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда

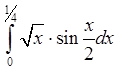
Решение

В разложении функции sin(x) в степенной ряд

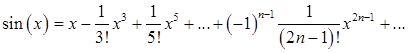
заменим 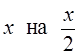. Тогда получим

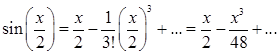
Умножая этот ряд почленно на будем иметь

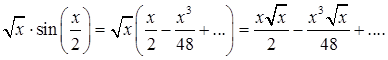
Следовательно


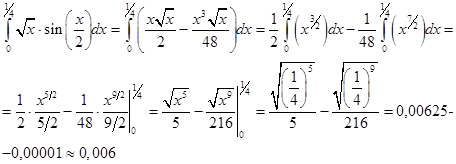
Ответ: »0,006.

Похожие работы

  • Формулы по математическому анализу

    Формулы дифференцирования Таблица основных интегралов Правила интегрирования Основные правила дифференцирования Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие

  • Билеты по математическому анализу

    Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № Сформулируйте понятие полного дифференциала функции двух переменных и объясните его геометрический смысл.

  • Нахождение площади живого сечения траншеи

    1. Формулировка проблемы. Сечение траншеи имеет форму близкую к сегменту параболы, ширина траншеи на её поверхности l метров наибольшая глубина H метров . найти площадь «живого сечения» траншеи , если она полностью заполнена водой.

  • Основные понятия математического анализа

    Определение определенного интеграла, правила вычисления площадей поверхностей и объемов тел с помощью двойных и тройных интегралов. Понятие и виды дифференциальных уравнений, способы их решения. Действия над комплексными числами, понятие и свойства рядов.

  • Функционально-графический подход к решению задач с параметрами

    Выполнение алгебраических преобразований, логическая культура и техника исследования. Основные типы задач с параметрами, нахождение количества решений в зависимости от значения параметра. Основные методы решения задач, методы построения графиков функций.

  • Интегралы. Функции переменных

    Метод интегрирования по частям. Задача на нахождение частных производных 1-го порядка. Исследование на экстремум заданную функцию. Нахождение частных производных. Неоднородное линейное дифференциальное уравнение 2-го порядка. Условия признака Лейбница.

  • Интегралы, объем тела вращения, метод наименьших квадратов

    Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.

  • Дифференциальные уравнения

    Вычисление первого и второго замечательных пределов, неопределенного и определенного интегралов, площади криволинейной трапеции, координат середин сторон треугольника с заданными вершинами. Определение критических точек и асимптот графика функции.

  • Определение интегралов

    Расчет неопределенных интегралов, проверка результатов дифференцированием. Вычислить по формуле Ньютона-Лейбница определенный интеграл. Вычисление площади фигуры, ограниченной заданной параболой и прямой. Общее решение дифференциального уравнения.

  • Техника интегрирования и приложения определенного интеграла

    Способы определения точного значения интеграла по формуле Ньютона-Лейбница и приближенного значения интеграла по формуле трапеций. Порядок нахождения координаты центра тяжести однородной плоской фигуры ограниченной кривой, особенности интегрирования.