Название: Теория вероятностей

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 84.22 Kb

Скачать файл: referat.me-217656.docx

Краткое описание работы: Общее решение дифференциального уравнения первого порядка. Уравнение с разделенными переменными. Выбор частного интеграла. Частное решение дифференциального уравнения второго порядка. Вероятность проявления события, интегральная формула Муавра-Лапласа.

Теория вероятностей

Содержание

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Список используемой литературы

Задание 1

Найти общее решение дифференциального уравнения первого порядка:

.

Решение:

Преобразуем уравнение и разделяя переменные, получим уравнение с разделенными переменными:

Интегрируем его и получаем общее решение данного уравнения

Ответ: Общее решение данного уравнения

Задание 2

Найти общее решение дифференциального уравнения первого порядка:

.

Решение:

Вводим замену

→

Так как одну из вспомогательных функций можно взять произвольно, то выберем в качестве какой-нибудь частный интеграл уравнения . Тогда для отыскания получим уравнение . Итак, имеем систему двух уравнений:

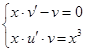
Далее

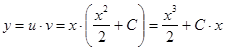
Проверка:

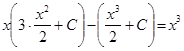
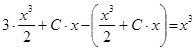
верное тождество. Ч. т.д.

Ответ:

Задание 3

Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям:

,

Решение:

Общее решение данного уравнения

ищется по схеме:

Находим общее решение однородного уравнения. Составим характеристическое уравнение

и

Общее решение имеет вид:

,

где

Находим частное решение . Правая часть уравнения имеет специальный вид. Ищем решение

, т.е.

Найдем производные первого и второго порядков этой функции.

-2
1
1

	→
	→
	→

Т.о. частное решение

Общее решение

Используя данные начальных условий, вычислим коэффициенты

Получим систему двух уравнений:

→

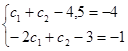
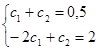
Искомое частное решение:

Ответ:

Задание 4

В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в мягком переплете. Библиотекарь взял 2 учебника. Найти вероятность того, что оба учебника в мягком переплете.

Решение:

Пусть имеется множествоN элементов, из которых M элементов обладают некоторым признаком A . Извлекается случайным образом без возвращения n элементов. Вероятность события, что из m элементов обладают признаком А определяется по формуле:

(N=6, M=3, n=2, m=2)

Ответ:

Задание 5

Дана вероятность появления события A в каждом из независимых испытаний. Найти вероятность того, что в этих испытаниях событие A появится не менее и не более раз.

Решение:

Применим интегральную формулу Муавра-Лапласа

Где

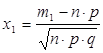и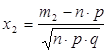

Ф ( x) - функция Лапласа 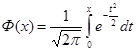, обладает свойствами

1⁰ . - нечетная, т.е.

2⁰ . При , значения функции представлены таблицей (табулированы) для

Так

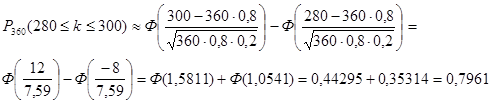
Ответ:

Задание 6

Задан закон распределения дискретной случайной величины X (в первой строке указаны возможные значения величины X, во второй строке даны вероятности p этих значение).

Xi	8	4	6	5
pi	0,1	0,3	0,2	0,4

Найти:

1) найти математическое ожидание ,

2) дисперсию ;

3) среднее квадратичное отклонение .

Математическое ожидание (ожидаемое среднее значение случайной величины):

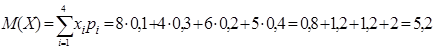
Дисперсия ( мера рассеяния значений случайной величины Х от среднего значения а ):

.

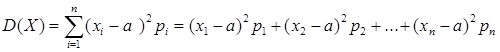Второй способ вычисления дисперсии:

где

.

Среднее квадратичное отклонение (характеристика рассеяния в единицах признака Х ):

→

Ответ:

Математическое ожидание

Дисперсия

Среднее квадратичное отклонение

Задание 7

Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно 0,25 мм. Стандартными считаются детали, размер которых заключен между 199,5 мм и 200,5 мм. Найти процент стандартных деталей.

Решение:

Таким образом, процент стандартных деталей составляет 95,45%

Ответ: Стандартных деталей 95,45%.

Список используемой литературы

1. Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением MS Excel. /Под ред. Г.В. Гореловой, И.А. Кацко. - Ростов н/Д: Феникс, 2006. - 475 с.

2. Ковбаса С.И., Ивановский В.Б. Теория вероятностей и математическая статистика: Учебное пособие для экономистов. - СПб.: Альфа, 2001. - 192 с.

3. Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика: Учебник. - М.: ФОРУМ, 2008. - 200 с.

4. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник. - М.: ЮНИТИ-ДАНА, 2007. - 551 с.

5. Пехлецкий И.Д. Математика. / Под ред. И.Д. Пехлецкого. - М.: Издательский центр "Академия", 2003. - 421с.

6. Пугачев В.С. Теория вероятностей и математическая статистика: Учебное пособие. - М.: ФИЗМАТЛИТ, 2002. - 496 с.