Referat.me
/ / Контрольная работа

Название: Контрольная работа

Вид работы: реферат

Рубрика: Математика

Размер файла: 46.82 Kb

Скачать файл: referat.me-216901.docx

Краткое описание работы: 385. Вычислить несобственные интегралы или установить их расходимость. По определению несобственного интеграла имеем: Интеграл сходится. 301. Найти неопределенный интеграл.

Контрольная работа

№385. Вычислить несобственные интегралы или установить их расходимость.


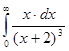По определению несобственного интеграла имеем:


Интеграл сходится.

№301. Найти неопределенный интеграл.


Представим подинтегральную функцию в виде слагаемых



№522. Даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.



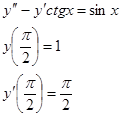Понизим порядок дифференциального уравнения, т.е. введем новую функцию , тогда

и получаем уравнение


Это линейное уравнение первого порядка.

Введем новые функции u=u(x) и v=v(x).

Пусть , тогда , т.е.


(1)


Предположим, что функция такова, что она обращает в тождественный нуль выражение, стоящее в круглых скобках уравнения (1) т.е., что она является решением дифференциального уравнения.


это уравнение с разделяющимися переменными



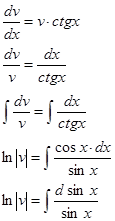Здесь

Подставляем значение v в уравнение (1), получаем


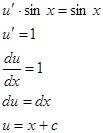Следовательно,


а т.к. , то


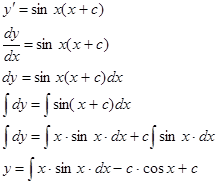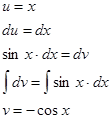решим отдельно интеграл

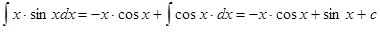, тогда


общее решение данного дифференциального уравнения.

Найдем частное решение при заданных условиях


Т.к. , то


Т.к. , то


- частное решение при заданных условиях.

№543. Даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.


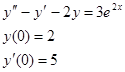Составим характеристическое уравнение


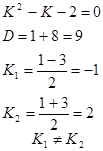Т.к. , то общее решение запишется в виде


Найдем частное решение т.к. в правой части стоит , то


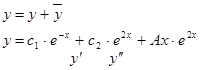Найдем и


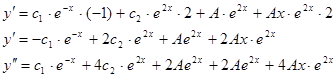
Подставим значение и в данное уравнение, получим:


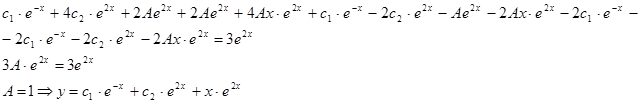Общее решение данного дифференциального уравнения.

Найдем частное решение при заданных начальных условиях

, т.к. , то

, т.к. , то

решаем систему


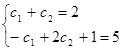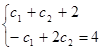и


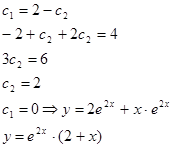- частное решение при заданных начальных условиях.

Похожие работы

  • Определенный интеграл

    Определенный интеграл Содержание Лекция 1. Определенный интеграл 1. Понятие определенного интеграла 2. Геометрический смысл определенного интеграла

  • Криволинейный интеграл первого и второго рода

    Криволинейный интеграл первого рода Криволинейный интеграл второго рода Задача приводящая к понятию криволинейного интеграла. Определение криволинейного интеграла по координатам.

  • Некоторые приложения определенного интеграла в математике

    Некоторые приложения определенного интеграла в математике Курсовая работа студента гр. МТ-21 Нургалиев А.З. Павлодарский университет Павлодар 2005 год.

  • Решение дифференциальных уравнений

    Задачи на нахождение неопределенного интеграла с применением метода интегрирования по частям. Вычисление площади, ограниченной заданными параболами. Решение дифференциального уравнения первого порядка. Исследование на сходимость ряда; признаки сходимости.

  • Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых)

    Лабораторная работа № 4. Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых). Гребенникова Марина 12-А класс Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

  • Интегралы, зависящие от параметра

    Министерство образования и науки РФ Федеральное Агентство по образованию ГОУ ПВО «Таганрогский государственный педагогический институт» Курсовая работа

  • Интегралы. Функции переменных

    Метод интегрирования по частям. Задача на нахождение частных производных 1-го порядка. Исследование на экстремум заданную функцию. Нахождение частных производных. Неоднородное линейное дифференциальное уравнение 2-го порядка. Условия признака Лейбница.

  • Интегралы, объем тела вращения, метод наименьших квадратов

    Неопределенный интеграл. Объем тела вращения. Эмпирическая формула. Сходимость ряда. Вычисление объема тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. Исследование на условную сходимость по признаку Лейбница.

  • Техника интегрирования и приложения определенного интеграла

    Способы определения точного значения интеграла по формуле Ньютона-Лейбница и приближенного значения интеграла по формуле трапеций. Порядок нахождения координаты центра тяжести однородной плоской фигуры ограниченной кривой, особенности интегрирования.

  • Несобственные интегралы

    Дисциплина: «Высшая математика» Тема: «Несобственные интегралы» 1. Несобственные интегралы с бесконечными пределами При введении понятия определенного интеграла, а также при рассмотрении задач, связанных с ним, все время делалось предположение, что область интегрирования конечна, а интегрируемая функция на нем непрерывна.