Название: Вычисление емкости

Вид работы: статья

Рубрика: Математика

Размер файла: 57.87 Kb

Скачать файл: referat.me-215288.docx

Краткое описание работы: Для расчета емкости можно ввести разность потенциалов между обкладками, решить уравнение Пуассона, найти D на обкладках, а затем плотность поверхностного заряда обкладок σ = ± Dn (Dn - это Dx или Dr у обкладки).

Вычисление емкости

.

М.И. Векслер, Г.Г. Зегря

Для расчета емкости можно ввести разность потенциалов между обкладками, решить уравнение Пуассона, найти D на обкладках, а затем плотность поверхностного заряда обкладок σ = ± Dn (Dn - это Dx или Dr у обкладки). При этом принимается, что поле вне конденсатора отсутствует (иначе неверна связь σ и Dx(r)).

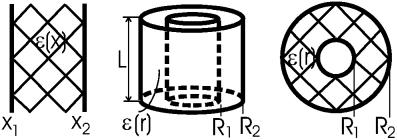
Рассмотрим для примера симметричный (ε = ε(r)) цилиндрический конденсатор. В нем

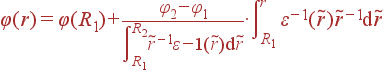(39)

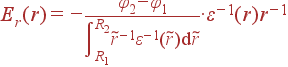(40)

|σ (R1(2))| = |Dr(R1(2))| = ε0ε(R1(2))|Er(R1(2))|

(41)

Заряд обкладки равен

|Q| = |σ1(2)|· 2π R1(2)L = |Dr(R1(2))|· 2π R1(2)L

(42)

где L - длина конденсатора вдоль оси z. Как видно, R1 или R2 cокращается, после чего можно найти емкость как

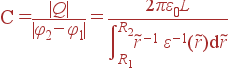(43)

Аналогичное рассмотрение для декартового и сферического случаев приводит к выражениям:

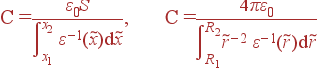(44)

Если имеет место зависимость проницаемости от других координат типа ε(r, z, φ) = f1(r)· f2(z, φ), то приведенные выше формулы верны для малого элемента площади обкладок dzR1dφ, а для нахождения емкости всего конденсатора необходимо произвести интегрирование:

(45)

Краевыми эффектами во всех случаях пренебрегается.

Задача: Найти емкость цилиндрического конденсатора, а также абсолютную величину заряда обкладок при подаче напряжения U. Радиусы обкладок R1 и R2, а длина L. Диэлектрик, заполняющий конденсатор, однороден, его проницаемость равна ε.

Решение: По формулам для емкости цилиндрического конденсатора

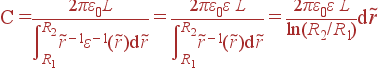получаем заряд:

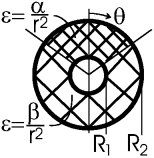
Задача. Часть сферического конденсатора (область θ<π/3) заполнена диэлектриком с проницаемостью ε(r) = α/r2, а остальная часть имеет ε(r) = β/r2. Найти емкость, если радиусы обкладок R1 и R2.

Решение: Описанное в задаче изменение проницаемости диэлектрика может быть представлено как ( является при этом кусочной функцией, принимающей значения α и β). Поэтому емкость можно вычислить как:

С	=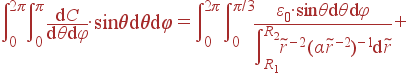
+

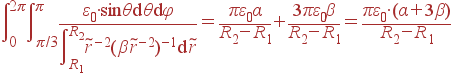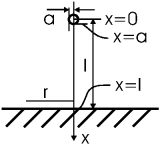
Задача. В диэлектрике проницаемости ε на расстоянии l от бесконечной проводящей плоскости расположен небольшой металлический шарик радиуса a<< l. Найти емкость системы.

Решение: Для нахождения емкости необходимо, задавшись зарядом шарика q, найти разность потенциалов между шариком и плоскостью.

Так как шарик очень маленький (a<< l), заряд на его поверхности можно считать равномерно распределенным (искажения его поля, вносимые плоскостью, заметны лишь на большом расстоянии от шарика).

Разность потенциалов можно найти как

где интеграл берется по любой траектории, соединяющей шарик и плоскость. Разумеется, удобнее взять простейшую траекторию: перпендикуляр, опущенный из шарика на плоскость. Введем ось x по этому перпендикуляру так, что центр шарика имеет координату 0, а плоскость x = l.

Для нахождения поля системы применяется метод изображений. На оси x получается:

Теперь записываем разность потенциалов:

Последнее приближенное равенство получено с учетом условия a<< l. Теперь емкость

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.