Расчет электрических полей при наличии диэлектриков. Поляризованность. Связанный заряд.

М.И. Векслер, Г.Г. Зегря

Уравнения Максвелла

(28)

и уравнение Пуассона

(29)

применимы при наличии любых диэлектриков. Следует только помнить, что ε может зависеть от координат, и его в общем случае нельзя выносить из-под знака div. Если при решении уравнения Пуассона потенциал φ найден на отдельных участках, то "сшивка" осуществляется согласно условиям

(30)

Теорема Гаусса как математический закон не теряет свой силы при наличии диэлектриков, но для ее практического использования не только плотность заряда ρ, но и ε должны иметь высокосимметричное распределение. Например, в случае сферической симметрии ε, как и ρ, должен зависеть только от r.

Интегрирование закона Кулона в системах с диэлектриками является недопустимым, за исключением одной искусственной ситуации. Если ε = const во всем пространстве (кроме проводников), то в задачах для вакуума просто заменяем ε0 на произведение ε0ε. В частности, для точечного заряда .

Реакция диэлектрика на электрическое поле заключается в поляризации диэлектрика - ориентации дипольных моментов его молекул по полю. Количественно этот эффект тем сильнее, чем выше диэлектрическая проницаемость и чем сильнее поле. Поляризованные молекулы сами являются источниками поля, которое накладывается на внешее поле, что осложняет ситуацию даже при простой геометрии.

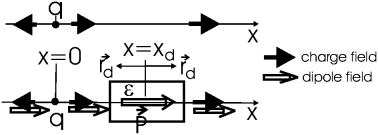Задача: Диэлектрический брусок внесен в поле точечного заряда. В какую сторону (качественно) изменится поле на прямой заряд-брусок в сравнении с тем, каким оно было бы при отсутствии бруска?

Решение - Диэлектрический брусок поляризуется в поле - возникает диполь , ориентированный от заряда q, если q>0. Поле этого диполя накладывается на поле заряда. Направим ось x от заряда в сторону диполя и введем вектор от диполя в точку, где оценивается поле. Тогда , для x>xd и для x<xd (xd - координата диполя). По формуле получаем, что поле диполя в любом месте оси x направлено в сторону ее положительного направления. Это означает, что при x>0 поле точечного заряда q, существовавшее без диэлектрика, возрастет, а при x<0 - уменьшится.

Количественные характеристики поляризации - вектор поляризованности и связанный заряд ρ '.

ρ '

=

Места локализации связанного заряда:

- там, где есть свободный заряд ρ

- там, где ε≠ const (диэлектрик неоднороден)

σ ' может быть отлична от 0 (т.е. ρ ' = ∞):

- там, где есть σ (например, обкладки конденсатора)

- там, где имеет место разрыв ε (стык диэлектриков).

Суммарный связанный заряд, проинтегрированный по всему объему тела, равен 0 - иначе тело оказывается изначально заряженным.

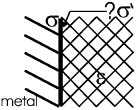Задача. Найти плотность связанного заряда у границы металла с диэлектриком (ε). Заряд металла σ.

Ответ: .

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.