Название: Вычисление двойных интегралов методом ячеек

Вид работы: реферат

Рубрика: Математика

Размер файла: 54.41 Kb

Скачать файл: referat.me-215394.docx

Краткое описание работы: МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Чувашский государственный университет им. И. Н. Ульянова КУРСОВАЯ РАБОТА по вычислительной математике.

Вычисление двойных интегралов методом ячеек

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Чувашский государственный университет им. И. Н. Ульянова

КУРСОВАЯ РАБОТА

по вычислительной математике.

Вычисление двойных интегралов методом ячеек.

Выполнил студент

факультета ИиВТ,

группа ИВТ-11-00

Борзов Леонид

Чебоксары-2002

Содержание.

Теоретическая часть…………………………………………3

Задание………………………………………………………..4

Текст программы. ……………………………………………5

Блок-схема программы…………………….………………...6

Выполнение программы в математическом пакете………..7

Список использованной литературы……………………......8

Теоретическая часть.

Численные методы могут использоваться для вычисления кратных интегралов. Ограничимся рассмотрением двойных интегралов вида

I = (1)

Одним из простейших способов вычисления этого интеграла является метод ячеек . Рассмотрим сначала случай, когда областью интегрирования G является прямоугольник: , .По теореме о среднем найдём среднее значение функции f ( x , y ) :

S =( b - a )( d - c ). (2)

Будем считать, что среднее значение приближённо равно значению функции в центре прямоугольника, т. е. . Тогда из (2) получим выражение для приближённого вычисления двойного интеграла:

(3)

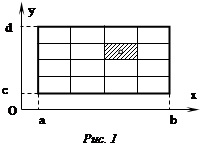
Точность этой формулы можно повысить, если разбить область G на прямоугольные ячейки D_ij (рис. 1): x_{i -1 i} (i =1,2,…,M), y_{i -1 i} (j =1,2,…,N). Применяя к каждой ячейке формулу (3), получим

òò_{D Gij} f ( x , y ) dxdy » ¦ ( ) D x_i D y_i .

Суммируя эти выражения по всем ячейкам, находим значение двойного интеграла:

_I , _j ) (4)

В правой части стоит интегральная сумма; поэтому при неограниченном уменьшении периметров ячеек (или стягивания их в точки) эта сумма стремится к значению интеграла для любой непрерывной функции f ( x , y ) .

Можно показать, что погрешность такого приближения интеграла для одной ячейки оценивается соотношением

R_ij » D x_i D y_{j .}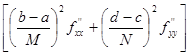

Суммируя эти выражения по всем ячейкам и считая все их площади одинаковыми, получаем оценку погрешности метода ячеек в виде

O ( D x ² + D y ² ) .

Таким образом, формула (4) имеет второй порядок точности. Для повышения точности можно использовать обычные методы сгущения узлов сетки. При этом по каждой переменной шаги уменьшают в одинаковое число раз, т. е. отношение M / N остаётся постоянным.

Если область G непрямоугольная, то в ряде случаев её целесообразно привести к прямоугольному виду путём соответствующей замены переменных. Например, пусть область задана в виде криволинейного четырёхугольника: , . Данную область можно привести к прямоугольному виду с помощью замены , . Кроме того, формула (4) может быть обобщена и на случай более сложных областей.

Задание .Найти при помощи метода ячеек значение интеграла , где – область, ограниченная функциями .

Текст программы.

#include<conio.h>

#include<iostream.h>

float f(float,float);

void main() {

const float h1=.0005,h2=.001;

float s1,x,y,i,I;

clrscr();

s1=h1*h2;

I=0;

y=h2/2;

x=1-h1/2;

for(i=0;i<1/h2;i++) {

while (y<2*x-1) {

I+=s1*f(x,y);

x-=h1;

}

y+=h2;

x=1-h1/2;

}

cout<<"Площадь интеграла равна: "<<I;

getch();

}

float f(float x,float y){

return x*x+y*y;

}

Блок-схема программы.

x=1-h1/2

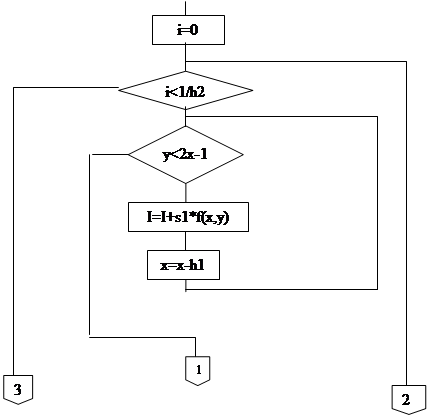Выполнение программы в математическом пакете.

h1=.0005;

h2=.001;

s1=h1*h2;

I=0;

y=h2/2;

x=1-h1/2;

for i=1:1/h2

while y<2*x-1 I=I+s1*(x*x+y*y);

x=x-h1;

end

y=y+h2;

x=1-h1/2;

end

disp('Площадь интеграла равна:');

disp(I);

В зависимости от шагов сетки получаем с различной точностью значение искомого интеграла

Площадь интеграла равна:

0.2190

Список использованной литературы.

1. Бахвалов Н.С. Численные методы. т.1 – М.: Наука. 1975.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1966.

3. Калиткин Н.Н Численные методы. – М.: Наука, 1978.

4. Турчак Л. И. Основы численных методов. – М.: Наука, 1987.