Название: Метод хорд
Вид работы: реферат
Рубрика: Математика
Размер файла: 466.65 Kb
Скачать файл: referat.me-215491.docx
Краткое описание работы: Метод хорд — один з поширених ітераційних методів. Його ще називають методом лінійного інтерполювання, методом пропорційних частин, або методом хибного положення.
Метод хорд
Метод хорд — один з поширених ітераційних методів. Його ще називають методом лінійного інтерполювання, методом пропорційних частин, або методом хибного положення.
Нехай задано рівняння
![]() ,
,
де ![]() на відрізку
на відрізку ![]() має неперервні похідні першого й другого порядків, які зберігають сталі знаки на цьому відрізку, і
має неперервні похідні першого й другого порядків, які зберігають сталі знаки на цьому відрізку, і![]() , тобто корінь
, тобто корінь ![]() рівняння відокремлений на
рівняння відокремлений на ![]() .
.
Ідея методу хорд в тому, що на досить малому відрізку дуга кривої ![]() замінюється хордою і абсциса точки перетину хорди з віссю
замінюється хордою і абсциса точки перетину хорди з віссю ![]() є наближеним значенням кореня.
є наближеним значенням кореня.
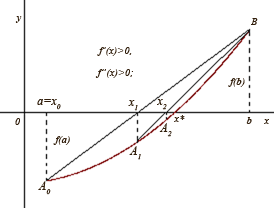
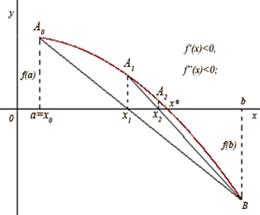
а б
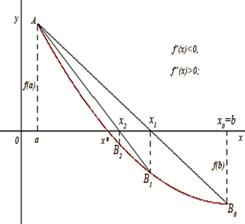
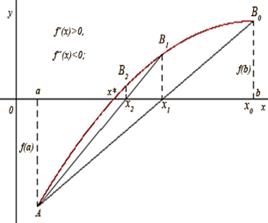
в г
рис.1
Нехай для визначеності![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1,а). Візьмемо за початкове наближення шуканого кореня
(рис. 1,а). Візьмемо за початкове наближення шуканого кореня ![]() значення
значення![]() . Через точки
. Через точки ![]() і
і ![]() проведемо хорду і за першенаближення кореня
проведемо хорду і за першенаближення кореня ![]() візьмемо абсцису
візьмемо абсцису ![]() точки перетину хорди з віссю
точки перетину хорди з віссю ![]() . Тепер наближене значення
. Тепер наближене значення ![]() кореня можна уточнити, якщо застосувати метод хорд до відрізка
кореня можна уточнити, якщо застосувати метод хорд до відрізка ![]() . Абсциса
. Абсциса ![]() точки перетину хорди
точки перетину хорди ![]() буде другим наближенням кореня. Продовжуючи цей процес необмежено, дістанемо послідовність
буде другим наближенням кореня. Продовжуючи цей процес необмежено, дістанемо послідовність ![]() наближених значень кореня
наближених значень кореня ![]() даного рівняння.
даного рівняння.
Для виведення формули методу хорд запишемо рівняння прямої, що проходить через точки ![]() і
і ![]() :
:
![]() .
.
Поклавши ![]() , знайдемо абсцису точки перетину хорди
, знайдемо абсцису точки перетину хорди ![]() з віссю
з віссю
![]() :
: ![]() .
.
Значення ![]() можна взяти за наступне наближення, тобто
можна взяти за наступне наближення, тобто
![]() , тобто
, тобто![]() = 0,1,2,
= 0,1,2,
У цьому разі і тоді, коли ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1, б) кінець
(рис. 1, б) кінець ![]() відрізка
відрізка ![]() є нерухомим.
є нерухомим.
Якщо ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1, в), або
(рис. 1, в), або ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1, г), аналогічно можна записати формулу:
(рис. 1, г), аналогічно можна записати формулу:
![]() , тобто
, тобто![]() = 0,1,2,... .
= 0,1,2,... .
У цьому випадку точка ![]() є нерухомим кінцем відрізка
є нерухомим кінцем відрізка ![]() .
.
У загальному випадку нерухомим буде той кінець відрізка ізоляції кореня, в якому знак функції ![]() збігається із знаком другої похідної, а за початкове наближення
збігається із знаком другої похідної, а за початкове наближення ![]() можна взяти точку відрізка
можна взяти точку відрізка ![]() , в якій
, в якій ![]() .
.
Отже, метод хорд можна записати так:
![]() , тобто
, тобто![]() = 0,1,2, (1)
= 0,1,2, (1)
де ![]()
З формули (1) видно, що метод хорд є методом ітерацій ![]() , в якому
, в якому
![]() (2)
(2)
Зауважимо, що рівняння ![]()
на відрізку ![]() рівносильне рівнянню
рівносильне рівнянню ![]() .
.
Достатні умови збіжності методу хорд дає така теорема.
Теорема. Нехай на відрізку ![]() функція
функція ![]() неперервна разом із своїми похідними до другого порядку включно, причому
неперервна разом із своїми похідними до другого порядку включно, причому ![]() , а похідні
, а похідні ![]() і
і ![]() зберігають сталі знаки на
зберігають сталі знаки на ![]() , тоді існує такий окіл кореня
, тоді існує такий окіл кореня ![]() рівняння
рівняння ![]() , що для будь-якого початкового наближення
, що для будь-якого початкового наближення ![]() з цього околу послідовність
з цього околу послідовність ![]() , обчислена за формулою (1), збігатиметься до кореня
, обчислена за формулою (1), збігатиметься до кореня ![]() .
.
Доведення. Для доведення теореми досить показати, що в деякому околі ![]() кореня
кореня ![]() похідна
похідна ![]() функції (2) задовольняє умову
функції (2) задовольняє умову ![]() для будь-яких
для будь-яких ![]() .
.
Обчислимо
![]() .
.
Поклавши ![]() і врахувавши, що
і врахувавши, що ![]() , маємо
, маємо
![]() . (3)
. (3)
Запишемо для ![]() в околі точки
в околі точки ![]() формулу Тейлора із залишковим членом у формі Лагранжа:
формулу Тейлора із залишковим членом у формі Лагранжа:
![]() ,
,
де ![]()
![]() лежить між
лежить між ![]() і
і ![]() .
.
Поклавши в ній![]() , дістанемо
, дістанемо
![]() , (4)
, (4)
Із формули (3), враховуючи (4), знаходимо ![]() .
.
Оскільки ![]() і
і ![]() — неперервні на
— неперервні на ![]() , то і
, то і ![]() буде неперервною на
буде неперервною на ![]() функцією, тому
функцією, тому ![]() .
.
Звідси і з неперервності ![]() випливає, що на відрізку
випливає, що на відрізку ![]() існує окіл
існує окіл ![]() точки
точки ![]() такий, що
такий, що ![]() для будь-якого
для будь-якого ![]() . Тоді з теореми про достатні умови методу ітерацій (Нехай рівняння
. Тоді з теореми про достатні умови методу ітерацій (Нехай рівняння ![]() має корінь
має корінь ![]() і в деякому околі
і в деякому околі ![]()
![]() цього кореня функція
цього кореня функція ![]() задовольняє умову Ліпшиця
задовольняє умову Ліпшиця ![]() , де
, де![]() ; тоді для будь-якого
; тоді для будь-якого ![]() послідовність
послідовність ![]() ,обчислена за формулою
,обчислена за формулою ![]() ,
, ![]() збігається до кореня
збігається до кореня ![]() , причому швидкість збіжності характеризується нерівністю
, причому швидкість збіжності характеризується нерівністю ![]() ) випливає, що послідовність {
) випливає, що послідовність {![]() }, обчислена за формулою (1), збігається до кореня
}, обчислена за формулою (1), збігається до кореня ![]() , якщо початкове наближення
, якщо початкове наближення ![]() . Теорему доведено.
. Теорему доведено.
Виведемо формулу, яка дає можливість оцінити абсолютну похибку наближення ![]() через два послідовні наближення
через два послідовні наближення ![]() і
і![]() .
.
Нехай ![]() — неперервна і зберігає на
— неперервна і зберігає на ![]() сталий знак, причому
сталий знак, причому
![]() , де
, де ![]() ,
, ![]() .
.
З формули
![]()
дістаємо ![]() .
.
Звідси, враховуючи, що ![]() ,
,
маємо ![]() .
.
Застосувавши теорему Лагранжа, дістанемо
![]() ,
,
де ![]() лежить між точками
лежить між точками ![]() і
і ![]() , а
, а ![]() — між
— між ![]() і
і ![]() . Далі запишемо:
. Далі запишемо:
![]() або
або ![]()
Оскільки ![]() зберігає на
зберігає на ![]() сталий знак, то
сталий знак, то ![]() .
.
Тому ![]() (5)
(5)
Якщо на відрізку ![]() справедлива нерівність
справедлива нерівність ![]() , то із (5) випливає оцінка:
, то із (5) випливає оцінка: ![]() .
.
Отже, корінь ![]() рівняння
рівняння ![]() буде знайдено методом хорд із наперед заданою точністю
буде знайдено методом хорд із наперед заданою точністю ![]() , якщо для двох послідовних наближень
, якщо для двох послідовних наближень ![]() і
і ![]() справджуватиметься нерівність
справджуватиметься нерівність
![]() .
.
Приклад 1.
Відокремити корені рівняння ![]() аналітично і уточнити один з них методом хорд з точністю до 0,01.
аналітично і уточнити один з них методом хорд з точністю до 0,01.
Розв’язання. Маємо функцію
![]() .
.
Похідна
![]() ;
; ![]() .
.
Складемо таблицю знаків функції ![]() :
:
| -1 | 0 | |||
| - | - | + | + |
Рівняння має один дійсний корінь, що лежить на проміжку ![]()
Щоб уточнити корінь, знаходимо другу похідну ![]() ; на проміжку
; на проміжку ![]() виконується нерівність
виконується нерівність ![]() .
.
Для обчислень використаємо формулу
![]() , де
, де ![]() .
.
Результати обчислень розміщуємо в таблиці.
0 1 2 3 4 |
0 -0,882 -0,943 -0,946 -0,946 |
0 -0,6861 -0,8386 -0,8466 |
0 0,7779 0,8892 0,8949 |
0 0,1556 0,1778 0,1790 |
0 -0,441 -0,4715 -0,473 |
1,5 0,2173 0,0121 0,0014 |
1,7 0,4173 0,2121 0,2014 |
1 0,118 0,057 0,054 |
-0,118 -0,057 -0,054 -0,054 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Відповідь. Приклад 2.
Відокремити корені рівняння Розв’язання.
рис.2 Таким чином, додатний коріньрівняннязнаходиться на проміжку
при Для обчисленьзастосуємо формулу
Розрахунки зручно розмістити в таблиці:
Відповідь: Задачі для самостійного розв’язування. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) ![]() ,
,
![]() ;
;
2) ![]() ,
,
![]() ;
;
3) ![]() ,
,
![]() ;
;
4) ![]() ,
,
![]() ;
;
5) ![]() ,
,
![]() ;
;
6) ![]() ,
,
![]() ;
;
7) ![]() ,
,
![]() ;
;
8) ![]() ,
,
![]() ;
;
9) ![]() ,
,
![]() ;
;
10) ![]() ,
,
![]() ;
;
11) ![]() ,
,
![]() ;
;
12) ![]() ,
,
![]() ;
;
13) ![]() ,
,
![]() ;
;
14) ![]() ,
,
![]() ;
;
15) ![]() ,
,
![]() ;
;
16) ![]() ,
,
![]() ;
;
17) ![]() ,
,
![]() ;
;
18) ![]() ,
,
![]() ;
;
19) ![]() ,
,
![]() ;
;
20) ![]() ,
,
![]() ;
;
21) ![]() ,
,
![]() ;
;
22) ![]() ,
,
![]() ;
;
23) ![]() ,
,
![]() ;
;
24) ![]() ,
,
![]() ;
;
25) ![]() ,
,
![]() ;
;
26) ![]() ,
,
![]() ;
;
27) ![]() ,
,
![]() ;
;
28) ![]() ,
,
![]() ;
;
29) ![]() ,
,
![]() ;
;
30) ![]() ,
,
![]() ;
;
31) ![]() ,
,
![]() ;
;
32) ![]() ,
,
![]() ;
;
33) ![]() ,
,
![]() ;
;
34) ![]() ,
,
![]() ;
;
35) ![]() ,
,
![]() ;
;
36) ![]() ,
,
![]() ;
;
37) ![]() ,
,
![]() ;
;
38) ![]() ,
,
![]() ;
;
39) ![]() ,
,
![]() ;
;
40) ![]() ,
,
![]()
Похожие работы
-
Цілочислове програмування
Постановка задачі Існує доволі широкий клас задач математичного програмування, в економіко – математичних моделях яких одна або кілька змінних мають набувати цілих значень, наприклад, коли йдеться про кількість верстатів у цеху, тобто коли така вимога випливає з особливостей технології виробництва.
-
Решение нелинейных уравнений
Задание №1 Отделить корни уравнения графически и уточнить один из них: · методом половинного деления; · методом хорд; · методом касательных; · методом секущих;
-
Решение нелинейных уравнений с одной переменной
Раздел 2. Численные методы Тема 1. Решение нелинейных уравнений с одной переменной 1.1. Постановка задачи При решении ряда задач физики, механики и техники возникает необходимость решения уравнений с одной переменной. В общем случае нелинейное уравнение можно записать в виде: F(x)=0, где функция F(x) определена и непрерывна на промежутке {a, b}.
-
Наближене обчислення означених інтегралів формули прямокутників трапецій Сімпсона
Пошукова робота на тему: Наближене обчислення означених інтегралів: формули прямокутників, трапецій, Сімпсона. План Наближене обчислення означених інтегралів
-
Нелинейное уравнение и интервал изоляции корня
Изучение методов уточнения корней нелинейных уравнений (половинного деления, хорд, касательных, простой итерации). Метод хорд и касательных дает высокую скорость сходимости при решении уравнений, и небольшую - метод половинного деления и простой итерации.
-
Приближенное вычисление корней в уравнения
Приближённое решение уравнений: метод хорд, метод касательных, комбинированный способ.
-
Приближенное решение уравнений методом хорд и касательных
Магнитогорский государственный технический университет Приближенное решение уравнений методом хорд и касательных Подготовил: Григоренко М.В. Студент группы ФГК-98
-
Метод хорд
Министерство образования и науки РФ Рязанская Государственная Радиотехническая Академия Кафедра САПР ВС Пояснительная записка к курсовой работе по дисциплине ,,Информатика”
-
Загальні положення теорії ймовірностей та математичної статистики
Реферат на тему: Загальні положення теорії ймовірностей та математичної статистики План Основні поняття та визначення: поняття стохастичної с-ми експерименту, ймовірності, випадкової величини.
-
Решение нелинейных уравнений
Графическое решение нелинейного уравнения. Уточнение значение одного из действительных решений уравнения методами половинного деления, Ньютона–Рафсона, секущих, простой итерации, хорд и касательных, конечно-разностным и комбинированным методом Ньютона.
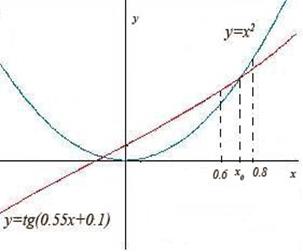 Відокремимо корінь графічно. Побудуємо графіки функції
Відокремимо корінь графічно. Побудуємо графіки функції