Название: Функция плотности распределения

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 260.64 Kb

Скачать файл: referat.me-216017.docx

Краткое описание работы: Графическое изображение теоретической и эмпирической функций плотности распределения; критерии их согласования. Определение доверительных интервалов для математического ожидания. Расчет диапазона рассеивания значений при заданной вероятности риска.

Функция плотности распределения

Задание

номер интервала	границы интервалов t		частота m
	свыше	до(включительно)
1	57,997	57,999	2
2	57,999	58,001	2
3	58,001	58,003	8
4	58,003	58,005	25
5	58,005	58,007	33
6	58,007	58,009	50
7	58,009	58,011	65
8	58,011	58,013	71
9	58,013	58,015	32
10	58,015	58,017	37
11	58,017	58,019	26
12	58,019	58,021	6
13	58,021	58,023	3

1. Определение теоретической функции плотности распределения. Графическое изображение эмпирического и теоретического распределений

плотность распределение доверительный математический ожидание

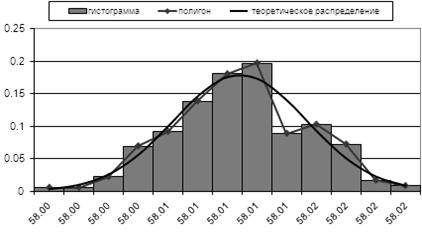
При построении гистограмм и полигонов по оси абсцисс откладывают значения результатов измерений (середины интервалов x_i ), по оси ординат – частности появления результатов измерения в каждом i-м интервале.

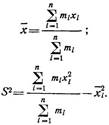
Из-за ограниченности числа результатов измерений при обработке вместо математического ожидания и дисперсии получают их приближенные оценки– соответственно эмпирическое среднее и эмпирическую дисперсию S² , характеризующие средний результат измерений и степень разброса измерений. и S² определяются из выражений:

Значения вероятности попадания результата измерения в конкретный интервал можно определить, используя значения функции:

,

где .

Тогда вероятность попадания результата в i-й интервал величиной h

.

Внесем все вычисления в таблицу и на основании полученных результатов построим кривую теоретического распределения, а так же гистограмму и полигон эмпирического распределения:

Середина интервала xi	Эмпирич. частости P’i	mi xi	xi -	zi	mi xi 2	φi (z)	Pi
								57,998	0,006	115,996	-0,01285	2,874965	6727,536	0,006399	0,002863
58	0,006	116	-0,01085	2,4275	6728	0,020956	0,009377
58,002	0,022	464,016	-0,00885	1,980034	26913,86	0,056179	0,025138
58,004	0,069	1450,1	-0,00685	1,532569	84111,6	0,123277	0,055162
58,006	0,092	1914,198	-0,00485	1,085103	111035	0,221427	0,099081
58,008	0,139	2900,4	-0,00285	0,637638	168246,4	0,325553	0,145674
58,01	0,181	3770,65	-0,00085	0,190173	218735,4	0,391793	0,175314
58,012	0,197	4118,852	0,00115	0,257293	238942,8	0,385954	0,172701
58,014	0,089	1856,448	0,00315	0,704758	107700	0,311212	0,139257
58,016	0,103	2146,592	0,00515	1,152223	124536,7	0,20541	0,091914
58,018	0,072	1508,468	0,00715	1,599689	87518,3	0,110976	0,049658
58,02	0,017	348,12	0,00915	2,047154	20197,92	0,049077	0,02196
58,022	0,008	174,066	0,01115	2,494619	10099,66	0,017765	0,007949
Сумма	20883,91	1211493

=	58,01085
S2 =	1,99775E-05
S=	0,00446962

2. Критерий согласия эмпирического и теоретического распределений

Считают, что эмпирическое распределение хорошо согласуется с теоретическим, если (1 - g) больше 0,1. Согласно критерию Колмогорова, сравнивают эмпирические и теоретические значения, но уже не плотности распределения, а интегральной функции. Значение максимальной (по абсолютной величине) разности между ними D_N подставляют в выражение:

,

где N – объем выборки.

Вычисление эмпирических F’_i и теоретических F_i значений интегральной функции производим путем последовательного суммирования соответственно значений P’_i и P_i . Результаты вычислений сведены в таблицу:

Номер интервала	Pi	P’i	Fi	F’i	Fi-Fi'
1	0,002863	0,005556	0,002863	0,005556	0,002692
2	0,009377	0,005556	0,01224	0,011111	-0,00113
3	0,025138	0,022222	0,037379	0,033333	-0,00405
4	0,055162	0,069444	0,092541	0,102778	0,010237
5	0,099081	0,091667	0,191622	0,194444	0,002823
6	0,145674	0,138889	0,337295	0,333333	-0,00396
7	0,175314	0,180556	0,512609	0,513889	0,00128
8	0,172701	0,197222	0,68531	0,711111	0,025801
9	0,139257	0,088889	0,824566	0,8	-0,02457
10	0,091914	0,102778	0,91648	0,902778	-0,0137
11	0,049658	0,072222	0,966138	0,975	0,008862
12	0,02196	0,016667	0,988098	0,991667	0,003568
13	0,007949	0,008333	0,996048	1	0,003952

D_N = F'₈ – F₈ =0,025801,

N=åm_i =360,

Тогда получаем:

λ= 0,48953

Для l_N =0,52 g» 0,05 Þ (1 – 0,05)=0,95 >0,1.

Отсюда можно сделать вывод: согласие эмпирического распределения с нормальным теоретическим можно считать хорошим.

3. Определение доверительных интервалов

В ряде задач, особенно при малом числе измерений, требуется не только найти эмпирическую оценку для того или иного параметра, но и определить доверительный интервал, в котором с доверительной вероятностью будет находиться теоретическое значение параметра.

Доверительный интервал для математического ожидания определяем из выражения:

интегральный доверительный интервал математический ожидание

Значения t_γ табулированы и равняется t_γ = 2,18 для N=13 и γ*=0,95.

58,00814756<M<58,01355244

Доверительный интервал для среднего квадратического отклонения определяем из выражения:

Значения χ₁ ² , χ₂ ² табулированы и определяется в зависимости от числа измерений N и односторонних вероятностей γ₁ , γ₂ :

Значение χ₁ ² определяем при вероятности (1- γ₁ ), χ₂ ² – при γ₂ .

χ₁ ² =24,1 χ₂ ² =4,18

И тогда

0,003024897

<σ<

0,008194587

4. Определение диапазона рассеивания значений

Определение границ диапазона рассеивания значений по результатам измерений, при вероятности риска 0,0027 .

М » = 58,01085

» S = 0,00446962

М-3 » 57.997442

М+3 » 58.024258

Определение границ диапазона рассеивания значений по результатам измерений, при допускаемом значении вероятности риска 2β=0,001

М±σ

=0,4995 при этом=3,29 (по справочнику)

М-3,29=57,996146

М+3,29=58,025554

Список использованной литературы

1. Зябрева Н.Н. и др. Пособие к решению задач по курсу "Взаимозаменяемость, стандартизация и технические измерения". Учеб. Пособие для вузов. М., "Высш. школа", 1977.