Referat.me
/ / Законы распределения случайных величин. Доверительный интервал

Название: Законы распределения случайных величин. Доверительный интервал

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 46.3 Kb

Скачать файл: referat.me-214576.docx

Краткое описание работы: Определение вероятности появления события в каждом из независимых испытаний. Случайные величины, заданные функцией распределения (интегральной функцией), нахождение дифференциальной функции (плотности вероятности), математического ожидания и дисперсии.

Законы распределения случайных величин. Доверительный интервал

Контрольная работа по дисциплине:

Теория вероятностей и математическая статистика

Законы распределения случайных величин. Доверительный интервал

Задача 1

Вероятность появления события в каждом из независимых испытаний равна 0,8. Найти вероятность того, что в 100 испытаниях событие появится не менее 70 и не более 80 раз.

Решение :

,

где 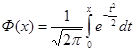- функция Лапласа, значения которой находятся из таблиц.

;

.

Здесь: .

.

Ответ: 0,49.

Задача 2

Среднее число вызовов, поступающих на АТС на 1 минуту, равно двум. Найти вероятность того, что за 4 минуты поступит: а) 3 вызова; б) не менее 3-х вызовов; в) менее 3-х вызовов. Предполагается, что поток вызовов – простейший.

а) Вероятность события «за 4 минуты поступило 3 вызова равна:

,

где

- среднее число вызовов в минуту; ;

t – время, за которое может поступить 3 вызова; t=4 мин.;

k – число возможных вызовов за время t; k=3.

.

- находим из таблицы значений функции распределения Пуассона для k=3 и a==8.

в) События «поступило менее 3-х вызовов» и «поступило не менее 3-х вызовов» являются противоположными. Поэтому найдем сначала вероятность первого события:

.

Здесь: вероятности находятся из таблиц распределения Пуассона соответственно для значений k=0, k=1, k=2 и для a==8.

б) Данное событие является противоположным к событию, описанному в пункте в) (выше), поэтому: .

Ответ : а) 0,03; б) 0,99; в) 0,01.

Задание 3

Случайная величина Х задана функцией распределения (интегральной функцией) f(x). Требуется: а) найти дифференциальную функцию f¢(x) (плотность вероятности); б) найти математическое ожидание и дисперсию Х; в) построить графики функций f(x) и f¢(x).


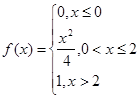
Решение:

а) 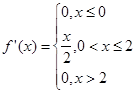- плотность вероятности.

б) Математическое ожидание:

.

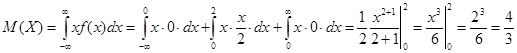Дисперсия величины Х:


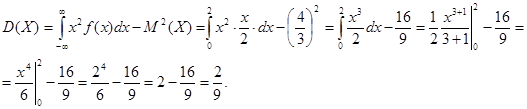
в) График функции f(x):

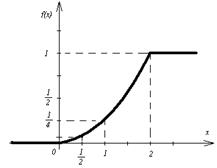
х 1 2
f(х) 1

; ; .

График функции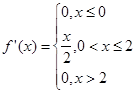

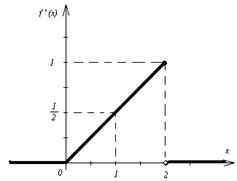
х 1 2
f¢(х) 1

; .

Задание 4

Найти доверительный интервал для оценки математического ожидания Q нормального распределения с надежностью , зная выборочную среднюю , объем выборки n и среднее квадратическое отклонение s.

; ; n=225.

Решение:

.

Здесь: находится из таблицы распределения Стьюдента для n=225 и .

.

;

.

Ответ: (73,12; 77,04).

Похожие работы

  • Шпаргалка по Теории Вероятности

    1) свойство вероятности: 20 стр. Свойство 1. Вероятность невозможного события равна 0, т.е. Свойство 2. Вероятность достоверного события равна 1, т.е.

  • Ряд распределения функция распределения

    Задача 1 (5) Производится контроль партии из 4 изделий. Вероятность изделия быть неисправным равна 0,1. Контроль прекращается при обнаружении первого неисправного изделия. Х – число обследованных приборов. Найти:а) ряд распределения Х б)функцию распределения F(X), в ответ ввести F(3.5). в) m(x) г) d(x) д) p(1.5<X<3.5).

  • Контрольная по теории вероятности

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ Факультет заочного и послевузовского обучения КОНТРОЛЬНАЯ РАБОТА №1

  • Теория вероятности

    Дискретные случайные величины и их распределения. Формула полной вероятности и формула Байеса. Общие свойства математического ожидания. Дисперсия случайной величины. Функция распределения случайной величины. Классическое определение вероятностей.

  • Предельные теоремы. Характеристические функции

    Теория вероятностей и закономерности массовых случайных явлений. Неравенство и теорема Чебышева. Числовые характеристики случайной величины. Плотность распределения и преобразование Фурье. Характеристическая функция гауссовской случайной величины.

  • Моделирование дискретной случайной величины по геометрическому закону распределения

    Распределение дискретной случайной величины по геометрическому закону распределения, проверка теоремы Бернулли на примере моделирования электрической схемы. Математическое моделирование в среде Turbo Pascal. Теоретический расчёт вероятности работы цепи.

  • Теория вероятностей

    Основы комбинаторики. Комбинаторика это раздел математики в котором изучается вопрос о том сколько различных комбинаций подчиненных тем или иным условиям можно составить из конечного числа различных элементов.

  • Определение законов распределения случайных величин и их числовых характеристик на основе опытны

    Самарский государственный аэрокосмический университет им. академика С.П. Королева Кафедра прикладной математики Расчетно-графическая работ по курсу «Теория вероятностей и математическая статистика»

  • Функция плотности распределения

    Графическое изображение теоретической и эмпирической функций плотности распределения; критерии их согласования. Определение доверительных интервалов для математического ожидания. Расчет диапазона рассеивания значений при заданной вероятности риска.

  • Проверка гипотезы о законе распределения случайной величины по критерию Пирсона

    Случайная выборка объема как совокупность независимых случайных величин. Математическая модель в одинаковых условиях независимых измерений. Определение длины интервала по формуле Стерджесса. Плотность относительных частот, критерий согласия Пирсона.