Название: Алгебра
Вид работы: книга
Рубрика: Математика
Размер файла: 444.23 Kb
Скачать файл: referat.me-216341.pdf
Краткое описание работы: ˛˜¯—˘ ˝¨¯ 6 ª º ß 3 6.1 ˚ º ª º . . . . . . . . . . . . . . . . . . . . . . 3 6.2 º ŁŁ æ æ Œ . ` . ı ˆ 6
Алгебра
˛˜¯—˘ ˝¨¯
6 ª º ß 3
6.1 ˚ º ª º . . . . . . . . . . . . . . . . . . . . . . 3
6.2 º ŁŁ æ æ Œ . ` . ı ˆ 6
6.3 ˜ ºŁ æ ª º . ˝˛˜ Ł ˝˛˚ . . . . . . . . . . . . 9
6.4 ˝ Ł Ł æ . ˚ Ł æŒ º Ł . ˚ æ . . 20
6.5 ˇ Ł Ł Œ æ . . . . . . . . . . . . . . . . . . . 26
6.6 ºª Æ Ł æŒŁ Œ ß º . . . . . . . . . . . . . . . . 28
6.7 ª º ß Łæº ß Ł º Ł . . . . . . . . . . . . . 32
7 ˛æ ß ºª Æ Ł æŒŁ æ Œ ß 36
8 ¸Ł Ø ß æ æ 37
8.1 ˇ Ł ºŁ Ø ª æ æ . . . . . . . . . . . . . . . 37
8.2 ` Łæ ºŁ Ø ª æ æ . . . . . . . . . . . . . . . . 39
8.3 ¨ Ł ºŁ Ø ßı æ æ . . . . . . . . . . . . . 43
8.4 ˇ ı ª Æ Łæ Œ ª . Ł ı . . 47
8.5 ¸Ł Ø ß æ æ . . . . . . . . . . . . . . . . . . 50
9 ¸Ł Ø ß ß ºŁ Ø æ æ 58
9.1 ˇ æ æ Ł ºª Æ ºŁ Ø ßı . . . . . . . 58
9.2 Ł ºŁ Ø ª Œ ºŁ Ø
æ æ . . . . . . . . . . . . . . . . . . . . . . . . . . 62
9.3 — ª Ł Œ ºŁ Ø ª . . . . . . . . . . . . . 68
9.4 ˛Æ Ł æ ºŁ Ø ª . . . . . . . . . . . . . . 71
1
2 ˛˜¯—˘ ˝¨¯
9.5 Œ Łæ Ł æŒŁØ ª º Ł ß Ł ºŁ Ø ª -
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
9.6 Ææ ß Œ ß Ł æ Ææ ß Ł ºŁ Ø ª
Ł Ł ß . . . . . . . . . . . . . . . . . . . . . 76
ˆº 6
ª º ß
6.1 ˚ º ª º
ˇ æ k Œ ŁŒæŁ º .
˛ º Ł 6.1.1. ª º Ł æ ª x Œ º k ß æ º ß Ł Ł
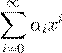 ,
,
ª x æŁ º Ł æ ª , αi º ß º k , Ł æ ß
0, æ (∃ n ∈ N) (∀ i > n ) αi = 0.
´ º Øł ª º ß Æ Æ f (x ), g (x ), h (x ), f 1 (x ), f 2 (x ),...ŁºŁ Œ f , g , h , f 1 , f 2 ,...
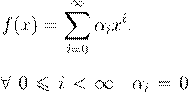 (6.1)
(6.1)
¯æºŁ ª º (6.1), ª º Æ ß º ß Ł Æ 0.
˛ º Ł 6.1.2. º ª ß αi x i Æ ß º Ł ª -
º (6.1), º ß αi Æ ß Œ Ł Ł Ł ª º
(6.1).
3
¯æºŁ ª º (6.1) ∀ i > n αi = 0, Æ Łæ :
![]() ŁºŁ f
(x
) = α
0
+ α
1
x
+ ··· + αn
xn
.
(6.2)
ŁºŁ f
(x
) = α
0
+ α
1
x
+ ··· + αn
xn
.
(6.2)
i =0
˙ æ Ł ı ŁæŁ (6.1) Œ ŁæŁ (6.2) ß Łł α 0 æ α 0 x 0 . ˇ Ł α 0 ß æ æ Æ ß º ª º f (x ).
˛ º Ł 6.1.3. º ª ª º f (x ) ß æ ŁÆ º łŁØ ºŁ ª º Œ Ł Ł ª ª º .
˛Æ Ł degf (x ) æ ª º f (x ).
¯æºŁ ŁæŁ (6.2) αn 6= 0, æ ª º f (x ) n , æ degf (x ) = n . ´ æº , αn xn ß æ æ łŁ º
ª º , αn ß æ æ łŁ Œ Ł Ł ª º .
æ æ ı ª º Ł æ ª x º k Æ -
æ k [x ] Ł ß æ Œ º ª º º k .
ˇ æ
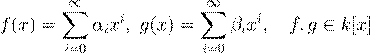 .
.
˛ º Ł 6.1.4. ˜ ª º f (x ),g (x ) ∈ k [x ] ß æ ß Ł, æºŁ ß æ Łı Œ Ł Ł ß Ł Ł Œ ßı æ ı x ,
æ (∀ 0 6 i < ∞) αi = βi .
´ æ k [x ] ŁŁ: æº Ł Ł Ł -
ª º .
˛ º Ł 6.1.5. Ø ı ª º f Ł g ß æ -
ª º
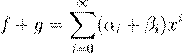 .
.
ˇ Ł Ł ı ª º f Ł g ß æ ª º
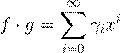 ,
ª γ
i
= X α
ν
β
µ
.
,
ª γ
i
= X α
ν
β
µ
.
νν,µ +µ >=0i
6.1. ˚ º ª º
˙ Ł 6.1.1. º º Ł , º ª , Æß
Ł ª º , æ Œ ßØ º ª ª º Ł Œ ßØ º ª ª º Ł Ł æ Ł Æß º ß.
˛ º Ł 6.1.5 Œ Œ æ ßæº , f + g Ł f · g Øæ Łº Æ ª º Ł. Œ Œ Œ f Ł g ª º ß, (∃ n ∈
∈ N) (∀ i > n ) αi = 0, βi = 0. ª (∀ i > n ) αi + βi = 0 ⇒ f + g
º æ ª º .
˜º f · g æ Ł γi , ∀ i > 2n . Œ Œ Œ i = ν + µ , Ł æº Ł
i > 2n ⇒ ν > n ŁºŁ µ > n ⇒ αν = 0 ŁºŁ βµ = 0 ⇒ γi = P αν βµ = 0 º i > 2n . , f · g º æ ª º . — ææ Ł æ æ Ł æ ß Ł Ł Ł ı ª º .
ˇ æ f 6= 0 Ł g 6= 0 ª º ß Ł k [x ],
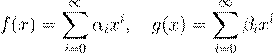 .
.
ˇ æ degf = n , æ αn 6= 0, degg = m , æ βm 6= 0. ˛Æ Ł
N = max(n,m ).
— ææ Ł
æ , 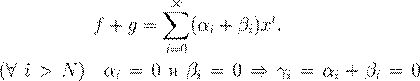 . º -
. º -
![]() º , deg(f
+ g
) 6 N
. ˙ Ł , deg(f
+ g
) 6 max(degf,
degg
). ˙ Œ
º , deg(f
+ g
) 6 N
. ˙ Ł , deg(f
+ g
) 6 max(degf,
degg
). ˙ Œ
æ æ Łª æ , Ł , Ł n 6= m .
— ææ Ł
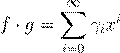 ª γ
i
= X α
ν
β
µ
.
ª γ
i
= X α
ν
β
µ
.
νν,µ +µ >=0i
¯æºŁ i > n + m , ν > n ŁºŁ µ > m ⇒ αν = 0 ŁºŁ βµ = 0 ⇒ γi = 0.
ˇ º degf · g 6 n + m . ˙ Ł , degf · g 6 degf + degg .
æ Ł
![]() .
.
Œ Œ Œ αn 6= 0 Ł βm 6= 0, αn βm 6= 0. ´ æº γn +m 6= 0 Ł
![]() degf
· g
= degf
+ degg
.
degf
· g
= degf
+ degg
.
6.2 º ŁŁ æ æ Œ . ` . ı ˆ
¯˛—¯ 6.2.1 ( º ŁŁ æ æ Œ ). ˇ æ k º , f Ł g ∈ k [x ], Ł g 6= 0. ª æ ø æ Ł æ ª -
º q,r ∈ k [x ] Œ ,
1) f = gq + r ;
2) r = 0 (ŁºŁ r 6= 0, degr < degg ).
˜ Œ º æ . I) ø æ Ł ª º q Ł r .
) ˇ æ f = 0 (ŁºŁ f 6= 0, degf < degg ). ´ æº Łæ f = 0 · g + f, (q = 0, r = f ). æº Ł 1) Ł 2) ß º ß.
Æ) f 6= 0 Ł degf > degg . ˇ æ
f = αn xn + ... + α 0 , αn 6= 0, g = βm xm + ... + β 0 , βm 6= 0.
degf = n, degg = m, n > m . ˇ æ Ł ª º
![]() (1)
(1)
| ª º f 1 æ Œ, Æß Ł Ł f . ¨ f 1 = 0 ŁºŁ f 1 6= 0 Ł degf 1 = n 1 < n . |
æ |
łŁØ º |
ª |
º |
| ¯æºŁ n 1 < m , ææ æ Ł ª |
º |
Π|
Ł |
. ¯æ- |
ºŁ n
1
> m
, , Æ ![]() æ łŁØ Œ Ł Ł f
1
, æ Ł
æ łŁØ Œ Ł Ł f
1
, æ Ł
ª º
![]() (2)
(2)
6.2. º ŁŁ æ æ Œ . ` . ı ˆ ˛ ª º f 2 æ Ł æ ŒŁ Æ , Æß Ł Ł æ -
łŁØ º ª º f 1 . ¨ f 2 = 0 ŁºŁ f 2 6= 0 Ł degf 2 = n 2 < n 1 .
¯æºŁ n 2 < m , ææ æ Ł ª º Œ Ł . ¯æºŁ n 2 > m , º Ł . .
˙ Ł , æ Ł ª º f , f 1 , f 2 , f 3 ,... Æ æ ª
Æß ø æº º æ º ßı Łæ º, ª Œ Œ -
º Ł n > n 1 > n 2 > ... > ns , ª ns < m .
![]() (s
)
(s
)
ª fs = 0 ŁºŁ fs 6= 0 Ł degfs = ns < m .
º Ł º æ æ (1), (2),..., (s ), º Ł
![]()
˛Æ Ł fs r , æ Ł æŒ ÆŒŁ q . ˇ º Ł r = f s −
![]()
![]() − qg
⇒ f
= qg
+ r
, æ º ŁºŁ æ 1), ª r
= 0 ∨ (r
6=
− qg
⇒ f
= qg
+ r
, æ º ŁºŁ æ 1), ª r
= 0 ∨ (r
6=
![]() 6= 0 ∧ degr <
degg
) æº Ł 2).
6= 0 ∧ degr <
degg
) æº Ł 2).
II) ¯ Ł æ æ q Ł r .
![]() ˜ æ Ł , æ Ø ª º q
Ł r
, æ º ßı æ Ł I), æ ø æ ª ª º q
Ł r
, º ø
˜ æ Ł , æ Ø ª º q
Ł r
, æ º ßı æ Ł I), æ ø æ ª ª º q
Ł r
, º ø
![]()
![]() æº Ł 1) Ł 2), æ f
= qg
+ r
Ł r
= 0 ∨ (r
= 06 ∧ degr <
degg
).
æº Ł 1) Ł 2), æ f
= qg
+ r
Ł r
= 0 ∨ (r
= 06 ∧ degr <
degg
).
¨
![]()
![]()
![]()
![]()
![]() qg
+ r
= qg
+ r
⇒ (q
− q
)g
= r
− r.
(∗) ˇ Œ , q
− q
= 0. ˜ æ Ł Ł , æ q
− q
6= 0. ˇ æ α
6= 0
æ łŁØ Œ Ł Ł ª ª º , ª æ łŁØ Œ -
qg
+ r
= qg
+ r
⇒ (q
− q
)g
= r
− r.
(∗) ˇ Œ , q
− q
= 0. ˜ æ Ł Ł , æ q
− q
6= 0. ˇ æ α
6= 0
æ łŁØ Œ Ł Ł ª ª º , ª æ łŁØ Œ -
![]() Ł Ł ª º (q
−q
)g
Æ αβm
6= 0. ¯æºŁ Æß αβm
= 0, α
= 0.
Ł Ł ª º (q
−q
)g
Æ αβm
6= 0. ¯æºŁ Æß αβm
= 0, α
= 0.
![]()
![]() ˙ Ł deg(q
− q
)g
= deg(q
− q
) + degg
> degg
.
˙ Ł deg(q
− q
)g
= deg(q
− q
) + degg
> degg
.
![]()
![]()
![]() ª Ø æ ß r
− r
= 0 ŁºŁ r
− r
6= 0,
deg(r
− r
) <
degg
. ß
ª Ø æ ß r
− r
= 0 ŁºŁ r
− r
6= 0,
deg(r
− r
) <
degg
. ß
º ŁºŁ, æ (∗)
æº æ Ł ª º , æ Œ ª ł degg
, æ æ Ł º Ø ª º ŁºŁ ª º , æ Œ ª ł degg
. Ł æ Ł Ł . ![]() ˛ º Ł 6.2.1. ´ Æ Ł ı ß 6.2.1 ª º ß q
Ł r
ß æ æ æ º ß æ ß Ł æ Œ º Ł
˛ º Ł 6.2.1. ´ Æ Ł ı ß 6.2.1 ª º ß q
Ł r
ß æ æ æ º ß æ ß Ł æ Œ º Ł
ª º f ª º g .
¯˛—¯ 6.2.2 (` ). ˛æ Œ º Ł ª º f (x ) x − γ Ł ª º f (x ) Ł x = γ , æ f (γ ).
˜ Œ º æ . ˇ æ f (x ) = q (x )(x − γ ) + r (x ), r (x ) = 0 ∨ (r (x ) 6= 6= 0 ∧ degr (x ) < 1). ˇ º r (x ) = 0 ∨ degr (x ) = 0, º Æ æº
r (x ) = r ∈ k .
ˇ æ q (x ) = β 0 +β 1 x +... +βs xs , ª f (x ) = q (x )·x −q (x )γ +r =
= β 0 x + β 1 x 2 + ... + βs xs +1 − β 0 γ − β 1 xγ − ... − βs xs γ + r .
æ Ł f (γ ) = β 0 γ +β 1 γ 2 +... +βs γs +1 −β 0 γ −β 1 γ 2 −... +βs γs +1 +r =
= r
. ŒŁ Æ , r
= f
(γ
). ![]()
ˇ æ º Ł æ º Ł ª º f (x ) (x − γ ) Œ ß Ø æı ˆ .
ˇ æ f (x ) = α 0 xn + α 1 xn −1 + ... + αn ,α 0 6= 0. — ºŁ f (x )
(x − γ ) æ æ Œ , º Ł f (x ) = q (x )(x − γ ) + r . ª º q (x )
Æ ŁæŒ Ł q (x ) = β 0 xn −1 + β 1 xn −2 + ... + βn −1 . ˝ ł Ø Ł Œ Ł Ł ß β 0 ,β 1 ,...,βn −1 Ł æ Œ r .
ˇ æ Ł æ ł Ł æ q
(x
)
Ł f
(x
)
Łı Ł . ¨ , ![]() . ˜
. ˜
| ª º |
ß ª Ł º Œ ª |
, Œ ª ß Łı Œ Ł Ł |
ß |
| Ł æ |
æ øŁı æ ı. |
Ł Œ Ł Ł ß. |
|
| x n : α 0 = β 0 |
⇒ β 0 = α 0 ; |
||
| x n −1 : α 1 = β 1 − β 0γ |
⇒ β 1 = β 0 γ + α 1 ; |
||
| x n −2 : α 2 = β 2 − β 1γ ... |
⇒ β 2 = β 1 γ + α 2 ; |
||
| x 1 : α n −1 = β n −1 − β n −2γ |
⇒ β n −1 = β n −2γ + α n −1; |
||
| x 0 : α n = r − β n −1γ |
⇒ r = βn −1 γ + αn . |
ŒŁ Æ Ł , Œ Ł Ł ß º ª æ ª Ł æ -
Œ ı æ æ ø Ł ßı ß Łæº ŁØ, Ł , Æß Ø-
Ł βk = βk −1 γ +αk . Ł ß Łæº Ł Æ Łæß Ł æº ø Ø æı ß ˆ .
| α 0 |
α 1 |
α 2 |
... |
α n −1 |
αn |
|
| γ |
α 0 |
β 0 γ + α 1 |
β 1 γ + α 2 |
... |
βn −2γ + αn −1 |
β n −1γ + α n |
| || |
|| |
|| |
|| |
|| |
||
| β 0 |
β 1 |
β 2 |
... |
β n −1 |
r = f (γ ) |
ˇ Ł : f (x ) = x 5 − 2x 4 + 3x 3 − 4x 2 + x − 1. ˝ Ø f (4).
| 1 |
−2 |
3 |
−4 |
1 |
−1 |
|
| 4 |
1 |
2 |
11 |
40 |
161 |
643 |
f (4) = 643, f (x ) = (x 4 + 2x 3 + 11x 2 + 40x + 161)(x − 4) + 643.
6.3 ˜ ºŁ æ ª º . ˝ ŁÆ º łŁØ ÆøŁØ ºŁ º Ł Ł ł Æø Œ
˛ º Ł 6.3.1. ˆ , ª º f (x ) ºŁ æ ª -
º g (x ) 6= 0 ŁºŁ, ª º g (x ) ºŁ ª º f (x ) ŁºŁ,
ª º g (x ) º æ ºŁ º ª º f (x ) ŁºŁ, ª º f (x ) Œ ª º g (x ) , æºŁ æ ø æ Œ Ø ª º q (x ) ,
f (x ) = q (x ) · g (x ).
˛ º Ł 6.3.2. ˆ , ª º f (x ) ºŁ æ ª º
g (x ) 6= 0, æºŁ æ Œ º Ł f (x ) g (x ) º .
, ª º g (x ) ºŁ f (x ) Æ æ Œ Œ g |f .
˛ º Ł 6.3.3. ˜ º ßı ª º f (x ) Ł g (x ) ß æ ææ ŁŁ ß Ł f ∼ g , æºŁ Ł ºŁ æ ª ª Ł º ß º Ø Œ æ , æ f = αg , α ∈ k ∗ = k {0}.
Øæ ºŁ æ Ł
1. (∀ f 6= 0) f |f .
2. (∀ g 6= 0) g |0.
3. ˜ º ßı ª º ææ ŁŁ ß ª Ł º Œ ª ,
| Œ ª Ł º |
ª ª , æ f ∼ g ⇔ f |g Ł g |f . |
|||
| 4. ¯æºŁ h |g , g |f , |
h |f ( Ł Ł æ ). |
|||
| 5. ¯æºŁ h |g , h |f , |
(∀ u,v ∈ k [x ]) h |(ug + vf ). |
|||
| 6. ˜ ºŁ º Ł |
º ßı Œ æ ª Æß º Œ |
º |
ß Œ |
- |
æ ß, æ æºŁ g |f Ł degf = 0, degg = 0.
7. ˝ º Œ æ ºŁ º Ø ª º , æ æºŁ
degg = 0, (∀ f ) g |f .
8. ¯æºŁ g |f Ł f 6= 0, degg 6 degf , Ł Œ æ æ Łª æ ª Ł º Œ ª , Œ ª g ∼ f .
9. ˛ ł Ł ºŁ æ Ł, æ ł Ł Œº ææ Ł ææ ŁŁ -
ßı ª º , æ æºŁ g |f , g 1 ∼ g , f 1 ∼ f , g 1 |f 1 .
˜ Œ º æ . 1) f (x ) = 1 · f (x ), æ f |f Ł q (x ) = 1.
2) 0 = 0 · g (x ), æ g |0 Ł q (x ) = 0.
3) ) ˝ Æı Ł æ .
ˇ æ f ∼ g , ª f = αg , ª α ∈ k ∗ , æ g |f Ł q = α . Œ Œ Œ
α 6= 0, g = α −1 f , æ f |g Ł q = α −1 .
b) ˜ æ æ .
ˇ æ g |f Ł f |g . ¨ , f = qg , g = q 1 f , æº º f = q (q 1 f ), æ (1−qq 1 )f = 0. Œ Œ Œ f 6= 0, 1−qq 1 = 0, æ qq 1 = 1. ˙ Ł degqq 1 = 0 ⇒ degq + degq 1 = 0 ⇒ degq = degq 1 = 0, æº º q Ł q 1 Œ æ ß. ¨ f = qg , ª q ∈ k ∗ ⇒ f ∼ g .
4) ¨ g = qh, f = q 1 g . ª f = q 1 (qh ) = (q 1 q )h ⇒ h |f .
5) ¨ g = qh , f = q 1 h . ª ug = uqh , vf = vq 1 h . — ææ Ł
ug + vf = (uq + vq 1 )h ⇒ h |(ug + vf ).
6) ¨ degf = 0 Ł f = qg ⇒ degf = degq + degg = 0 ⇒ degq = = degg = 0, æ q Ł g Œ æ ß.
7) Œ Œ Œ degg = 0, g ∈ k ∗ , æ ø æ g −1 ∈ k ∗ . ª
f = (fg −1 )g ⇒ g |f .
8) ¨ f = qg ⇒ degf = degg + degq ⇒ degf > degg . ´Ł ,
| Œ æ Æ ß º æ ª = 0 ⇒ q ∈ k ∗ ⇔ f ∼ g . |
Ł º Œ ª |
, Œ ª degq = |
| 9) ¨ f = qg , g = αq 1 , f = βf 1 , ª |
α,β ∈ k ∗ . ª |
βf 1 = qαg 1 ⇒ |
⇒ f
1
= (β
−1
qα
)g
1
⇒ g
1
|f
1
. ![]()
| ´ º Øł Æ ææ Ł Œ |
æŁæ ª |
º |
|
| {f 1 ,f 2 ,...,fs }, æ Ł Œ ßı Œ Ø Ø º . |
Ł ª º |
ºŁ |
|
| ˛ º Ł 6.3.4. ª º d ß |
æ |
ÆøŁ ºŁ º |
æŁæ - |
| ß ª º {f 1 ,f 2 ,...,fs }, æºŁ æŁæ ß, æ (∀ 1 6 i 6 s ) d |fi . |
ºŁ |
æ ª º ß |
Ø |
| ¯˛—¯ 6.3.1 ( æŁº ßı |
æº |
Ł ı, º |
øŁı |
| ˝˛˜). ˇ æ {f 1 ,f 2 ,...,fs } æŁæ |
ª |
º , æ Ł Œ |
ßı |
| Œ Ø Ø Ł ª º ºŁ |
º , Ł d Œ |
ßØ |
|
| º Ø ª º (d 6= 0). — æŁº Ł : |
ß æº |
øŁ |
- |
| 1) æ Œ æ ºŁ º Ø ª º |
d æ |
æ æ Œ |
æ |
| ÆøŁı ºŁ º Ø æŁæ ß ª º |
{f 1 ,f 2 ,...,fs }; |
||
| 2) ª º d º æ ÆøŁ ºŁ |
º æŁæ ß ª |
º |
|
{f 1 ,f 2 ,...,fs }, Œ ßØ ºŁ æ º Æ Ø ª Ø ÆøŁØ ºŁ º Ø æŁæ ß.
˜ Œ º æ . 1) ⇒ 2)
Œ Œ Œ æ Ł ºŁ º Ø ª º d ı Ł æ æ ª º d , æº Ł 1), d º æ ÆøŁ ºŁ º {f 1 ,f 2 ,...,fs }.
ˇ æ d 0 º Æ Ø ÆøŁØ ºŁ º {f 1 ,f 2 ,...,fs }, ª
æº Ł 1) d 0 æ æ Ł Ł ºŁ º Ø ª º d , æ d
ºŁ æ d 0 .
2) ⇒ 1)
´ß º Ł æº Ł 1) æ Ł ł ª . ) ˇ æ d 0 º Æ Ø ºŁ º ª º d . ¨ d 0 |d , æº Ł
2) (∀ 1 6 i 6 s ) d |fi ⇒ (∀ 1 6 i 6 s ) d 0 |fi , æ d 0 º æ ÆøŁ
ºŁ º æŁæ ß ª º {f 1 ,f 2 ,...,fs }.
Æ) ˛Æ . ˇ æ d 0 º Æ Ø ÆøŁØ ºŁ º æŁæ ß ª º
{f
1
,f
2
,...,fs
}. ª æº Ł 2) ª º d
ºŁ æ d
0
, æ d
0
º æ ºŁ º ª º d
. ![]()
˛ º Ł 6.3.5. ˝ ŁÆ º łŁ ÆøŁ ºŁ º (˝˛˜) æŁæ ß
ª º {f 1 ,f 2 ,...,fs }, ß æ º Æ Ø º Ø ª º d , º øŁØ º Æ Ł æŁº ßı æº ŁØ ß 6.3.1.
˛ º Ł 6.3.6. ˝˛˜ æŁæ ß ª º ß æ Œ Ø ÆøŁØ ºŁ º Ø æŁæ ß, Œ ßØ ºŁ æ º Æ Ø ª Ø ÆøŁØ ºŁ º Ø æŁæ ß ª º .
º æ Ł 6.3.1.1. ¯æºŁ ˝˛˜ æŁæ ß ª º æ ø æ ,
º æ æ ææ ŁŁ æ Ł.
˜ Œ º æ . ˇ æ d 1 , d 2 ˝˛˜ æŁæ ß ª º
f 1 ,f 2 ,...,fs , Æ ææ Ł d 1 Œ Œ ˝˛˜ æŁæ ß, d 2 Œ Œ ˛˜ æŁæ ß f 1 ,f 2 ,...,fs . ª º Ł 6.3.6 d 2 |d 1 . ˇ º Ł d 1 Ł d 2 , æ d 1 Æ ææ Ł Œ Œ ˛˜, d 2 Œ Œ ˝˛˜
æŁæ ß f
1
,f
2
,...,fs
. ˇ º Ł 6.3.6 d
1
|d
2
, ª 3 æ Øæ ºŁ æ Ł d
1
∼ d
2
. ![]()
´ ŁŒ æ æ ßØ æ: æ ø æ ºŁ ˝˛˜ æŁæ ß ª º {f 1 ,f 2 ,...,fs }? ˛ æ º Ł º ßØ. Æ Ł æ æ º º æŁæ ß Ł 2-ı ª º . ß Œ æ ø æ Ł ˝˛˜ 2-ı ª º Ł Œ ºª Ł ª ı Ł .
ºª Ł ß æ ºª Ł ¯ ŒºŁ Ł æ æº º ª º Ł . ˇ æ f Ł g º ßı ª º , degf > degg . — ºŁ f g æ æ Œ , º Ł
f = q 1 g + r 1 , ª r 1 = 0 ŁºŁ (r 1 = 06 Ł degr 1 < degg ).
¯æºŁ r 1 = 0 , ææ º Ł Œ Ł æ . ¯æºŁ r 1 6= 0 , ºŁ g r 1 æ æ Œ , º Ł
g = q 2 r 1 + r 2 , ª r 2 = 0 ŁºŁ (r 2 = 06 Ł degr 2 < degr 1 ).
¯æºŁ r 2 = 0 , ææ º Ł Œ Ł æ . ¯æºŁ r 2 6= 0 , ºŁ r 1 r 2 æ æ Œ , º Ł
r 1 = q 3 r 2 + r 3 , ª r 3 = 0 ŁºŁ (r 3 = 06 Ł degr 3 < degr 2 ).
¨ Œ º . ´ ŁŒ æ: ł ææ Œ ŁºŁ Æ æŒ ? ˙ Ł , æ Ł æ Œ Æ æ ª Æß ø æº -
º æ º ßı Łæ º, Ł degg > degr 1 > degr 2 > degr 3 > ... , Œ Æß Æ æŒ Ø. ´ Œ Œ º -
Ł æ
r k −2 = q k r k −1 + r k ;
r k −1 = q k +1r k ,
ª rk æº ŁØ ßØ º æ Œ ºª Ł ¯ ŒºŁ .
¯˛—¯ 6.3.2. ˝ ŁÆ º łŁØ ÆøŁØ ºŁ º 2-ı º ßı ª -
º f Ł g æ ø æ Ł æº º æ Œ
ºª Ł ¯ ŒºŁ , Ł Œ ª º f Ł g .
˜ Œ º æ . ˙ Łł æ , º øŁ ºª Ł ¯ ŒºŁ
Œ ª º f Ł g
f = q 1 g + r 1 ⇒ r 1 = f − q 1 g ; (1) g = q 2 r 1 + r 2 ⇒ r 2 = g − q 2 r 1 ; (2) r 1 = q 3 r 2 + r 3 ⇒ r 3 = r 1 − q 3 r 2 ; (3)
...
r k −2 = q k r k −1 + r k ⇒ r k = r k −2 − q k r k −1; (k )
r k −1 = q k +1r k . (k + 1) ¨ æº ª æ Ł , rk |rk −1 .
¨ æ (k ) Ł , rk |rk −2 .
¨ æ (k − 1) Ł , rk |rk −3 .
... r k |r 2, r k |r 1
¨ æ (2) Ł , rk |g .
¨ æ (1) Ł , rk |f .
º º rk º æ ÆøŁ ºŁ º æŁæ ß ª º
{f,g }. ˇ æ d º Æ Ø ÆøŁØ ºŁ º {f,g }, ª
Ł æ (1) Ł , d |r 1 , Ł æ (2) Ł , d |r 2 ,
...
Ł æ (k ) Ł , d |rk , æ rk ÆøŁØ ºŁ º {f,g } , Œ ßØ ºŁ æ º Æ Ø ª Ø
ÆøŁØ ºŁ º {f,g
}. ª º Ł 6.3.6 rk
˝˛˜ {f,g
}. ![]()
ø æ Ł ˝˛˜ º Æ Ø Œ Ø æŁæ ß ª º æ -
ºŁ æ æº ø Ø Ø, Œ Œ ª ı -
Ł .
¯˛—¯ 6.3.3 ( Œ º ). ˝˛˜ Œ Ø æŁæ -
ß ª º æ ø æ Ł Ł æ ºŁ æ ł Ł
HOD {f 1 ,f 2 ,...,fs −1 ,fs } = HOD {HOD {f 1 ,f 2 ,...,fs −1 },fs }.
˜ Œ º æ . ˇ Ł Ł Ł æŒ Ø Ł Œ ŁŁ s . ¯æ-
ºŁ s = 2 , Ł ß Ł . ˇ º Ł ,
º (s − 1) ª º , æ ß º ª æ , æ ø æ ŁÆ º łŁØ ÆøŁØ ºŁ º d æŁæ ß ª º
{f 1 ,f 2 ,...,fs −1 }. ˛Æ Ł d ¯ = HOD {d,fs }. ¨ , d ¯|d, d ¯|fs ,
Œ ª (∀ 1 6 i 6 s − 1) d |fi , ª Ł Ł æ Ł ºŁ-
æ Ł (∀ 1 6 i 6 s − 1) d ¯|fi , d ¯|fs , æº º d ¯ º æ ÆøŁ ºŁ º {f 1 ,f 2 ,...,fs −1 ,fs }. ˇ æ d 0 º Æ Ø ÆøŁØ ºŁ º
{f 1 ,f 2 ,...,fs −1 ,fs }, ª (∀ 1 6 i 6 s − 1) d 0 |fi Ł d 0 |fs æº -
º d 0 º æ ÆøŁ ºŁ º {f 1 ,f 2 ,...,fs −1 }. ª º Ł 6.3.6 d 0 |d . ŒŁ Æ d 0 |d, d 0 |fs æº º d 0 º æ ÆøŁ ºŁ º {d,f s }. ª Ł º Ł 6.3.6 æº d 0 |d ¯ .
¨ Œ d ¯ º æ ÆøŁ ºŁ º {f 1 ,f 2 ,...,fs −1 ,fs } Ł d ¯ ºŁ æ º Æ Ø ÆøŁØ ºŁ º {f 1 ,f 2 ,...,fs −1 ,fs }. ª º Ł 6.3.6
d
¯
= HOD {f
1
,f
2
,...,fs
−1
,fs
}. ![]()
¯˛—¯ 6.3.4 (Œ Ł ŁØ ˝˛˜ æŁæ ß ª º ).
˜º ª Æß ª º d º ºæ ˝˛˜ æŁæ ß ª º
{f 1 ,f 2 ,...,fs } Æı Ł Ł æ , Æß ª º d Æߺ
˛˜ Ø æŁæ ß Ł Æß ºŁ Ø ß ºæ Ł ª º -
ß, æ (∃ u 1 ,u 2 ,...,us , ∈ k [x ]) d = u 1 f 1 + u 2 f 2 + ... + us fs .
˜ Œ º æ . 1) ˜ æ æ .
ˇ æ d º æ ˛˜ {f 1 ,f 2 ,...,fs } Ł ∃ u 1 ,u 2 ,...,us ∈ k [x ] d =
= u 1 f 1 +u 2 f 2 +... +us fs . ˇ æ d 0 º Æ Ø ÆøŁØ ºŁ º {f 1 ,f 2 ,...,fs }.
, (∀ 1 6 i 6 s ) d 0 |f i . ª 5 æ Øæ ºŁ-
æ Ł d 0 |(u 1 f 1 + u 2 f 2 + ... + us fs ), æ d 0 |d . ˇ º Ł 6.3.6 d = HOD {f 1 ,f 2 ,...,fs }.
2)˝ Æı Ł æ .
| ˇ æ d º æ |
˝˛˜ {f 1 ,f 2 ,...,fs }. |
ª |
d |
º |
æ ˛˜ |
|||
| {f 1 ,f 2 ,...,fs }. ˛æ |
æ Œ , d ºŁ |
Ø |
ß |
æ |
||||
| f 1 ,f 2 ,...,fs . æ Ł |
Π|
Ł |
æŒ Ø Ł |
Œ ŁŁ. |
||||
| ˇ æ |
s = 2. ˛Æ Ł |
f 1 = f,f 2 = g . ˙ Łł |
æ |
, |
º - |
|||
| ø |
ºª |
Ł |
¯ ŒºŁ |
. |
||||
| f = q 1 g + r 1 ; |
(1) |
|||||||
| g = q 2 r 1 + r 2 ; ... |
(2) |
|||||||
| r k −3 = q k −1r k −2 + r k −1; |
(k − 1) |
|||||||
| r k −2 = q k r k −1 + r k ; |
(k ) |
|||||||
| r k −1 = q k +1r k . |
(k + 1) |
|||||||
| ¨ |
æ |
, |
˝˛˜ d |
ª º {f,g } |
rk . ¨ |
æ |
(k ) Ł - |
|
| , |
||||||||
d = r k −2 − q k r k −1 = r k −2 − q k (r k −3 − q k −1r k −2) =
= (1 + qk qk −1 )rk −2 − qk rk −3 = ... = ug + vf.
ˇ º Ł , Ł ß æ ºŁ º æŁæ ß, æ æ ø Ø Ł (s − 1) ª º . ˜ Œ æ ºŁ æ º æŁæ , æ æ øŁı Ł s ª º . ˇ 6.3.3 ŁÆ º łŁØ ÆøŁØ ºŁ º d æŁæ ß ª º {f 1 ,f 2 ,...,fs } æ æ ˝˛˜
2-ı ª º {d 1 ,fs }, ª d 1 ˝˛˜ {f 1 ,...fs −1 }. ˇ º Ł Ł Œ ŁŁ æ ø æ ª º ß v 1 ,...,vs −1 ∈ k [x ] ŒŁ ,
d 1 = v 1 f 1 + v 2 f 2 + ... + vs −1 fs −1 . Œ Œ Œ d º æ ˝˛˜ {d 1 ,fs }, æ ø æ ª º ß w 1 ,w 2 ∈ k [x ] ŒŁ , d = w 1 d 1 +w 2 fs . ¨
d
= w
1v
1f
1 + ··· + w
1v
s
−1f
s
−1 + w
2f
s
= u
1f
1 + u
2f
2 + ...
+ u
s
f
s
. ![]() ˛ º Ł 6.3.7. ª º ß æ Ł ß , æºŁ ª æ łŁØ Œ Ł Ł 1.
˛ º Ł 6.3.7. ª º ß æ Ł ß , æºŁ ª æ łŁØ Œ Ł Ł 1.
æ , Œ Œº ææ ææ ŁŁ ßı ª º æ ø æ
Ł ßØ ª º . ´ æ æ Ł æ Ł ˝˛˜ æŁæ ß ª º -
, Œ ß º æ æ æ ææ ŁŁ æ Ł, æ ø æ Ł æ ßØ Ł ßØ ˝˛˜. Ł ßØ ˝˛˜
Æ Æ (f 1 ,f 2 ,...,fs ).
˛ º Ł 6.3.8. Łæ ª º {f 1 ,f 2 ,...,fs } ß æ Ł æ Ø æ Œ æ Ł, æºŁ Ł ßØ ˝˛˜
(f 1 ,f 2 ,...,fs ) = 1. ´ æº ı ª º ª , Ł Ł æ ß .
¯˛—¯ 6.3.5 (æ Øæ Ł æ ßı ª º ).
ºŁ ß æº øŁ Ł .
1. Łæ ª º {f 1 ,f 2 ,...,fs } Ł æ æ Œ æ Ł ª Ł º Œ ª , Œ ª Œ Łı ºŁ Ø Œ ÆŁ -
Ł Ł Ł , æ (∃ u 1 ,...,us ∈ k [x ]) u 1 f 1 +... +us fs = 1;
2. ¯æºŁ![]() ;
;
3. ¯æºŁ (f,h ) = 1 Ł (g,h ) = 1, (fg,h ) = 1;
4. ¯æºŁ h |fg Ł (h,g ) = 1 , h |f ;
5. ¯æºŁ h |f Ł g |f Ł (h,g ) = 1, hg |f .
˜ Œ º æ . 1) ˇ º Ł 6.3.4 d = 1. æ , d -
º æ ˛˜ æŁæ ß {f 1 ,f 2 ...,fs }, ª 6.3.4 d = 1 Æ
˝˛˜ {f 1,f 2 ...,f s } ª Ł º Œ ª , Œ ª æ ø æ ª º ß
u 1 ,u 2 ,...,us ∈ k [x ] ŒŁ , u 1 f 1 + ... + us fs = 1.
2) Œ Œ Œ HOD{f 1 ,f 2 ...,fs } = d , 6.3.4 æ ø æ
ª º ß u 1 ,u 2 ,...,us ∈ k [x ] ŒŁ , d = u 1 f 1 +... +us fs . — ºŁ
Æ æ Ł æ ![]() , Ł æ Øæ 1 æº ,
, Ł æ Øæ 1 æº ,
![]() .
.
3) Œ Œ Œ (f,g ) = 1, 6.3.4 ∃ u,v ∈ k [x ] 1 = uf +
+ vh . Œ Œ Œ (g,h ) = 1, (∃ u 1 ,v 1 ∈ k [x ]) 1 = u 1 g + v 1 h . ˇ º
Ł Ł æ ł Ł . 1 = (uu 1 )fg + (vu 1 g + uv 1 f + vv 1 h )h . ˇ
æ Øæ 1 Ł ºŁ Ø Œ ÆŁ Ł ª º fg Ł h
Ł Ł , æº º (fg,h ) = 1.
4) Œ Œ Œ (h,g ) = 1, ∃ u,v ∈ k [x ] uh + vg = 1. Ł Æ æ Ł ª æ f , º Ł uhf + vgf = f . Œ Œ Œ h |fg ,
fg = qh , ª uhf + vqh = f ⇒ (uf + vq )h = f ⇒ h |f .
5) Œ Œ Œ h |f , f = qh . ¨ g |qh Ł (g,h ) = 1, æ Øæ 4 º , g |q , æº º q = q 1 g . ŒŁ Æ f = q 1 gh ⇒
⇒ gh
|f
. ![]()
` ææ Ł æŁæ ª º {f 1 ,f 2 ,...,fs },
Œ ßØ Ł Œ ßı º . ˜º ŒŁı æŁæ ª º Ł º -
Ł Ł Ł ł ª Æø ª Œ ª (˝˛˚) æı , º ªŁ Ø Ł Ł ˝˛˜.
˛ º Ł 6.3.9. ª º m ß æ ÆøŁ Œ ß æŁæ ß
ª º {f 1,f 2,...,f s }, Œ ßØ Ł Œ ßı ºŁ º , æºŁ ºŁ æ æ ª º ß Ø æŁæ ß, æ (∀ 1 6 i 6 s ) f i |m .
¯˛—¯ 6.3.6. ˇ æ {f 1 ,f 2 ,...,fs } æŁæ º ßı ª -
º Ł m 6= 0 ( Œ ßØ º Ø ª º ). — æŁº ß æº øŁ Ł :
1) æ Œ æ Œ ßı ª º m æ æ æ Œ æ
˛˚ æŁæ ß ª º {f 1 ,f 2 ,...,fs };
2) ª º m º æ ˛˚ {f 1 ,f 2 ,...,fs }, Œ ºŁ º Æ ª ˛˚ Ø æŁæ ß.
| ˛ º |
Ł 6.3.10. ˝ Ł łŁ ÆøŁ Œ |
ß (˝˛˚) æŁæ |
ß |
|
| ª º |
{f 1 ,f 2 ,...,fs } ß |
æ º Æ Ø |
º Ø ª º |
m , |
| º |
øŁØ º Æ Ł |
æŁº ßı æº |
ŁØ ß 6.3.6. |
|
| ˛ º |
Ł 6.3.11. ˝˛˚ æŁæ |
ß ª º |
ß æ Œ |
Æ- |
| ø Œ |
Ø æŁæ ß, Œ |
ºŁ º Æ |
ª Æø Œ |
|
| Ø æŁæ |
ß ª º . |
|||
| º æ Ł |
6.3.6.1. ¯æºŁ ˝˛˚ æŁæ |
ß ª º |
æ ø æ , |
|
| º |
æ æ ææ ŁŁ |
æ Ł. |
||
¯˛—¯ 6.3.7. ¯æºŁ æ ø æ ˝˛˚ 2-ı º Æßı º ßı -
ª º , æ ø æ ˝˛˚ Ł º Æ Ø Œ Ø æŁæ ß ª º -
, Ł Ł æ æº ø Ł Œ Ł º :
HOK{f 1 ,f 2 ,...,fs −1 ,fs } = HOK{HOK{f 1 ,f 2 ,...,fs −1 },fs }.
6.3.7 æ Ł ı Ł ˝˛˚ æŁæ ß ª º Œ ı Ł ˝˛˚ 2-ı ª º .
¯˛—¯ 6.3.8. ¯æºŁ f Ł g º ßı ª º , Łı ˝˛˚
| ˜ Œ |
º æ |
. ˛Æ |
Ł |
ª |
º |
fg . ´Ł = m (f,g ) |
, |
![]() æ ø æ Ł
æ ø æ Ł ![]() .
.
![]()
Ł
![]()
| æ m º æ ˛˚ ª º {f,g }. ˇ æ M |
º Æ |
˛˚ {f,g }. |
| , M = uf, M = vg ⇒ uf = vg . — ª æ (f,g ). ˇ º Ł |
ºŁ |
Æ æ Ł |
![]() .
.
ˇ æ Øæ 2 ß 6.3.5 Ł ![]() . ˇ 4 æ Øæ -
. ˇ 4 æ Øæ -
ß 6.3.5 Ł ![]() . ª u
= (
. ª u
= (
![]() f,g
g
)
q. M
= uf
= (
f,g
g
)
q. M
= uf
= (
![]() f,g
fg
)
q
= mq
. ´Ł , m
|M
. ˇ º Ł 6.3.11 m
º æ ˝˛˚ {f,g
}.
f,g
fg
)
q
= mq
. ´Ł , m
|M
. ˇ º Ł 6.3.11 m
º æ ˝˛˚ {f,g
}. ![]()
6.4 ˝ Ł Ł æ . ˚ Ł æŒ º Ł . ˚ æ
ˇ æ f ª º º Ł º Ø æ Ł, α ∈ k ∗ = k {0 }. ¨ æ ,
α |f Ł αf |f .
˛ º Ł 6.4.1. Ł Ł º ß Ł ºŁ º Ł ª º f º Ł-
º Ø æ Ł ß æ º ß Œ æ ß Ł ª º ß, ææ ŁŁ ß æ ª º f .
º æ Ł . ˜ ºŁ º d ª º f º æ Ł Ł º ß ª Ł
º Œ ª , Œ ª 0 < degd < degf .
º æ Ł . ª º f º Ł º Ø æ Ł Ł Ł Ł º ß
ºŁ ºŁ ª Ł º Œ ª , Œ ª ª æ Ł Ł Ł Ł 2-ı ª º , æ Ł Œ ßı ł æ Ł ª º
f , æ (∃ u,v ∈ k [x ]) f = uv , ª degu, degv < degf .
˛ º Ł 6.4.2. ª º P º Ł º Ø æ Ł ß æ Ł Ł ß º k , æºŁ Ł Ł º º Œ Ł Ł º ß ºŁ ºŁ. ´ Ł æº , ª º P ß æ
Ł Ł ß .
˛ º Ł 6.4.3. ª º P º Ł º Ø æ Ł ß æ Ł Ł ß º k , æºŁ ª º æ Ł Ł º Ł Ł Ł 2-ı ª º , æ Ł Œ ßı ł æ Ł
ª º P .
˙ Ł 6.4.1. ˇ Ł Ł Ł æ Ł æ ø æ ŁæŁ æ-
ª º k
. Œ, Ł , ª º f
= x
2
−2 = (x
+√2)(![]() x
−√2)
x
−√2)![]()
Ł Ł º Q. ˝ Ł Ł º R.
˙ Ł 6.4.2. ª º ß 1-Ø æ Ł º æ Ł Ł ß Ł º Æß º .
æº Ł ª , ª º ß 1-Ø æ Ł Ł º Œ Ł-
Ł º ß ºŁ ºŁ.
¯˛—¯ 6.4.1 (æ Øæ Ł Ł ßı ª º ). ºŁ ß æº øŁ Ł :
1. ¯æºŁ ª º P º æ Ł Ł ß , Ł º Æ Ø ææ ŁŁßØ æ Ł ª º Œ º æ Ł Ł ß .
2. ¯æºŁ P Ł Ł ßØ ª º , f º Æ Ø ª º , ºŁÆ
(P,f ) = 1, ºŁÆ P |f .
3. ¯æºŁ P Ł Ł ßØ ª º Ł P |fg , P |f ŁºŁ P |g .
4. ¯æºŁ P Ł Q Ł Ł ßı ª º , ºŁÆ (P,Q ) = 1, ºŁÆ P Ł Q ææ ŁŁ ß.
˜ Œ º æ . 1) ˇ æ P Ł Ł ßØ ª º . — ææ Ł αP , ª α ∈ k ∗ . ˝ Œ , αP º æ Ł Ł ß . ˜ æ Ł Ł , æ αP æ Ł Ł º ßØ ºŁ º , æ
(∃ d ∈ k [x ]) d |αP , ª 0 < degd < degαP = degP . ¨ , d |αP Ł αP |P ⇒ d |P Ł 0 < degd < degP . Ł Ł Ł Ł æ Ł ª º P .
2) ˛Æ Ł (P,f ) = d . ¨ d |P . Œ Œ Œ P Ł Ł , d
º Æß Ł Ł º ß ºŁ º , æ ºŁÆ d = α ∈ k ∗ , ºŁÆ d ∼ P . ´ æº Ł (P,f ) = 1. ´ æº , Ł P |d
Ł d |f ⇒ P |f .
3) ˇ æ P |fg . ¯æºŁ P |f , æ Œ . ¯æºŁ P - f , æ Øæ 2 (P,f ) = 1. ¨ Œ, P |fg Ł (P,f ) = 1, ª æ Øæ 4 ß 6.3.5
P |g .
4) ˇ æ P Ł Q Ł Ł ßı ª º . ¯æºŁ (P,Q ) = 1 ,
æ Œ . ˇ æ (P,Q ) 6= 1, ª æ Øæ 2 P |Q . º Ł
P
Ł Q
, º Q
|P
⇒ P
∼ Q
. ![]()
¯˛—¯ 6.4.2 ( º ŁŁ Ł Ł ß Ł ºŁ).
¸ Æ Ø ª º f º Ł º Ø æ Ł º k Æß
æ º Ł f = αP 1 · P 2 · ... · Ps , ª α ∈ k ∗ , Pi Ł -
ß Ł Ł ß k ª º ß. æ º Ł Ł æ
æ æ Œ æº Ł æ Ł º Ø Ł Ł Æı Ł , Æß α º º æ æ łŁ Œ Ł Ł ª º f .
˜ Œ º æ . 1) ø æ Ł .
— ææ Ł æ M æ ı Ł ßı ºŁ º Ø º Ł-
º Ø æ Ł ª º f . ´ æ M ßÆ ª º
P 1 Ł ł Ø æ Ł. ˇ Œ , ª º P 1 º æ Ł-
Ł ß . ˜ æ Ł Ł , æ ª º P 1 º æ Ł Ł-
ß . º º P 1 = du , ª 0 < degd < degP 1 , Ł Ł
ßÆ ª º P 1 . ¨
f = P 1 f 1 , ª 0 6 degf 1 < degf. (1) ¯æºŁ degf 1 = 0 , ææ ß º Ł Ł Ł ßı Ł º Ø Œ Ł æ . ¯æºŁ degf 1 > 0 , æ ª º f 1 Ł ææ Ł , Ł æ ª º f . ˇ º Ł , ª º f 1 æ Ł ßØ Ł Ł ßØ Ł º P 2 . ` Ł
f 1 = P 2 f 2 , ª 0 6 degf 2 < degf 1 . (2)
¯æºŁ degf 2 = 0 , ææ ß º Ł Ł Ł ßı Ł º Ø -
Œ Ł . ¯æºŁ degf 2 > 0 , ææ º . ¨ Œ º . ´ Ł-
Œ æ: ł ææ Œ ŁºŁ Æ æŒ ? ˙ Ł , æ Ł ª º f 1 ,f 2 ,... Æ æ ª Æß ø æº º æ
º ßı Łæ º degf > degf 1 > degf 2 > ... , Œ Æß
Æ æŒ Ø. ´ Œ Œ º Ł
fs −1 = Ps fs , ª degfs = 0. (s )
, f s = α ∈ k ∗. ˇ Ł º æ æ
(1), (2),..., (s ), º Ł f = αP 1 ·P 2 ·... ·Ps . Œ Œ ŒPi º æ Łß Ł ª º Ł, æ Ł æ Œ Ł Ł ß Ł æ ł Ø æ Ł x , º Ł , α º æ æ łŁ Œ Ł Ł -
ª º f .
2) ¯ Ł æ æ .
ˇ æ æ æ º Ł f = αP 1 · P 2 · ... · Ps Ł æ
ª æ º Ł f = βQ 1 · Q 2 · ... · Qt , ª β ∈ k ∗ , Qj Ł ß Ł Ł ß k ª º ß. ª , Œ ßł , β º æ æ łŁ Œ Ł Ł ª º f , æ β = α .
f = αP 1 · P 2 · ... · Ps = βQ 1 · Q 2 · ... · Qt . (∗)
— æ (∗) Œ ß , P 1 |(Q 1 · Q 2 · ... · Qt ). ˇ æ Øæ 3 ß 6.4.1 (∃ 1 6 j 6 t ) P 1 |Qj . ` æ Ł , P 1 |Q 1 . ª
æ Øæ 4 ß 6.4.1 P 1 ∼ Q 1 . Œ Œ Œ Æ ª º Ł ß, P 1 = Q 1 . ª æ (∗) æ Œ ø P 1 . ˇ º Ł
P 2 · ... · Ps = Q 2 · ... · Qt . (∗∗)
ª º P 2 ææ Œ , Œ Œ æ ª º P 1 . — æ
(∗∗) Œ ß , P 2 |(Q 2 ·... ·Qt ) ⇒ (∃ 2 6 j 6 t ) P 2 |Qj . ` æ Ł , P 2 |Q 2 . ª P 2 ∼ Q 2 ⇒ P 2 = Q 2 . ¨ Œ º . ¯æºŁ s = t ,
Œ Œ º Ł Ps = Qs . ºŁ s 6= t ? ˇ º Ł , s < t , ª æ Œ ø æ
(∗) P 1 · P 2 · ... · Ps º Ł , 1 = Qs +1 · ... · Qt ª Æß
Œ Œ Œ æº æ Ł ª º º Ø æ Ł, æ ª -
º º Ł º Ø æ Ł. º ªŁ Æß Ł s > t ŒŁ
Æ Qj
æ ß Pi
, º Œ Łæ ß ª Œ . ![]()
¯˛—¯ 6.4.3 ( Œ Ł æŒ æ º ŁŁ). ¸ Æ Ø ª -
º f º Ł º Ø æ Ł º k Æß æ º
Ł ![]() , ª α
∈ k
∗
, Pi
ºŁ ß Ł ß , Ł Ł ß k
ª º ß, ki
∈ N. æ º Ł
, ª α
∈ k
∗
, Pi
ºŁ ß Ł ß , Ł Ł ß k
ª º ß, ki
∈ N. æ º Ł
Ł æ æ æ Œ æº Ł æ Ł º Ø Ł Ł α Æı Ł º æ æ łŁ Œ Ł Ł ª º f .
˜ Œ º æ . ˇ 6.4.2 Ł f = αP 1 ·P 2 ·... ·Ps . ˛Æœ Ł
æ º ŁŁ Ł Ł Ł Œ ßı Ł º Ø æ Ł,
º Ł
![]() .
.
![]()
˛ º Ł 6.4.4. ˇ æ º Ł ª º f
Ł ![]()
![]() ß æ Œ Ł æŒŁ æ º Ł ª º
ß æ Œ Ł æŒŁ æ º Ł ª º
f
. ª º ß![]() ß æ º ß Ł ºŁ º Ł
ß æ º ß Ł ºŁ º Ł
ª º f . ˝ º ß Łæº k 1 ,k 2 ,...,kt ß æ Œ æ Ł Ł Ł ßı ª º P 1 ,P 2 ,...,Pt ª º f .
ˇ æ γ ∈ k . ß ŁºŁ, ª º ß 1-Ø æ Ł Ł -
Ł ß º Æß º k . ´ æ æ Ł x − γ º æ Ł ß
Ł Ł ß k ª º , ª Ł Œ æ Ł
ª º x − γ ª º f .
˛ º Ł 6.4.5. ˚ æ º γ ∈ k ª º f ßæ Œ æ Ł Ł ª ª º x − γ ª º f .
˛ º Ł 6.4.6. º γ ∈ k ß æ Œ ª º
f (x ), æºŁ f (γ ) = 0.
ˇ º Ł 6.4.1. ˜º ª , Æß º γ ∈ k Æߺ Œ -
ª º f (x ) Æı Ł Ł æ , Æß ª º f ºŁºæ x − γ , æ , Æß º γ Ł º º Ł º Œ æ
ª º f .
˜ Œ º æ . ´ æ º , ` f (x ) = Q (x )(x − γ ) +
+ f
(γ
), ª (x
− γ
)|f
(x
) ⇔ f
(γ
) = 0, æ º Ł 6.4.6 γ
º æ Œ f
(x
). ![]()
º æ Ł . º γ ∈ k º æ Œ ª º f (x ) ª Ł º Œ ª , Œ ª º γ Ł º Œ æ ª º
f (x ).
˛ º Ł 6.4.7. ˚ γ ª º f (x ) ß æ æ ß , æºŁ Ł Œ æ .
ˇ æ Œ Ł æŒ æ º Ł ª º f Ł Ł
![]() ,
ª degPi
> 2.
,
ª degPi
> 2.
´Ł ,
deg ![]() æ
æ
k 1 + k 2 + ... + ks 6 degf.
æ , (∀ 1 6 i 6 s ) f (γi ) = 0, æ γ 1 ,γ 2 ,...,γs º æ Œ -
Ł ª º f . ¯æºŁ Œ ßØ Œ γi æ Ł ki , Łæº k 1 + k 2 + ... + ks Łæº Œ Ø ª º f æ Łı Œ æ Ø.
ˇ º Ł 6.4.2. Łæº Œ Ø ª º f (x ) æ Łı Œ -
æ Ø æı Ł æ ª º f .
| 6.5 |
ˇ |
Ł |
Ł Œ |
æ |
|
| ˇ æ |
k |
Π|
ŁŒæŁ |
Łæº |
º . |
![]() ˛ º Ł 6.5.1. ˇ Ł Ø ª ºß æ
˛ º Ł 6.5.1. ˇ Ł Ø ª ºß æ
ª º Ł
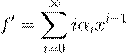 .
.
| ¯˛—¯ 6.5.1 ( æ |
ß Łº Ł |
Ł Ł ). |
| ¨ æ æº øŁ æ 1. α 0 = 0, ª α ∈ k ; 2. (αf )0 = αf 0 , ª α ∈ k ; 3. (f ± g )0 = f 0 ± g 0 ; 4. (fg )0 = f 0 g + fg 0 ; 5. (fn )0 = nfn −1 f 0 , n ∈ N. |
Øæ : |
|
| ˛ º Ł 6.5.2. ˇ º ª |
f (0) = f, f (l +1) = (f (l ))0, ª |
l > 0, l ∈ Z. |
| æ , æºŁ degf = n , |
(∀ l > n ) f (l ) = 0. |
|
| ¸ 6.5.1. ¯æºŁ f ª Ł degf 0 = n − 1. |
º º Ł º Ø æ |
Ł n , f 0 6= 0 |
˜ Œ º æ . ¨ f = αn xn +... +α 1 x +α 0 , ª αn 6= 0, n > 1. ˇ
º Ł 6.5.1 f 0 = nαn xn −1 +... +α 1 . łŁØ Œ Ł Ł -
ª º f 0 nαn , ª n ∈ N, αn 6= 0. ª nαn 6= 0, æº º
f
0
6= 0 Ł degf
0
= n
− 1. ![]()
¯˛—¯ 6.5.2. ˇ æ f ª º º Ł º Ø æ Ł Ł
Ł Ł ßØ Ł º P Ł º Ł º Œ æ k
ª º f . ª Ł Ł ßØ Ł º P Ł Œ æ k − 1 Ł Ø f 0 .
6.5. ˇ Ł Ł Œ æ
˜ Œ º æ . ¨ f = P l g , ª P - g . æ Ł f 0 = lP l −1 P 0 g +
+ P l g 0 = P l −1 (lP 0 g + Pg 0 ). ´Ł , P l −1 |f 0 , æ Œ æ P f 0 ł , l −1 . ˇ Œ , P l - f 0 . ˜ æ Ł Ł , æ
P l
|f
0
. ª P
|(lP
0
g
+ Pg
0
). ´Ł , P
|Pg
0
, æº º P
|(lP
0
g
). æ , (P,l
) = 1. ˇ º P
0
6= 0 Ł degP
0
<
degP
⇒ (P,P
0
) = 1. ˇ æ Øæ 3 ß 6.4.1 Ł , P
|g
, Ł Ł , . º º P l
- f
0
Ł Œ æ P
æ æ f
0
l
− 1
. ![]() º æ Ł
6.5.2.1.
º γ
Ł Œ æ k
ª º f
ª Ł
º æ Ł
6.5.2.1.
º γ
Ł Œ æ k
ª º f
ª Ł
º Œ ª , Œ ª f (γ ) = f 0 (γ ) = ... = f (k −1) (γ ) = 0, f (k ) (γ ) 6= 0.
˜ Œ º æ . 1) ˝ Æı Ł æ .
ˇ æ γ Ł Œ æ k ª º f . ˇ º Ł -
, (x − γ ) Ł Œ æ k ª º f . ˇ 6.5.2
x − γ Ł Œ æ k − 1 f 0 , x − γ Ł Œ æ k − 2 f 00 , ..., x −γ Ł Œ æ 1 f (k −1), x −γ Ł Œ æ 0 f (k ). ˇ Ł
º Ł 6.4.1 f (γ ) = f 0 (γ ) = ... = f (k −1) (γ ) = 0, f (k ) (γ ) 6= 0.
2) ˜ æ æ .
ˇ æ f (γ ) = f 0 (γ ) = ... = f (k −1) (γ ) = 0, f (k ) (γ ) 6= 0. ˇ æ Œ -
æ γ ª º f l .˝ Œ , l = k . ˜ æ Ł
Ł . ˇ æ , Ł , l < k . ª Ø æ Ł Œ º -
æ Æ Ł f (γ ) = f 0 (γ ) = ... = f (l −1) (γ ) = 0, f (l ) (γ ) 6= 0. ª
Æß , æº Ł f (l ) (γ ) = 0 Œ Œ Œ l 6 k −1. -
º ªŁ Ł Ł Œ Ł Ł Ł º Ł , l > k
. ![]()
º æ Ł 6.5.2.2. ˚ æ º γ ª º f Ł ł Œ Ł Ø ª º f , Ł ø ª γ æ Ł Œ .
¯˛—¯ 6.5.3 ( Æ º ŁŁ Œ ßı Ł º Ø). ˇ æ
f
ª º º Ł º Ø æ Ł º k
. ª ª º ![]() Ł æ ß Ł Ł ß Ł ºŁ, Ł
Ł æ ß Ł Ł ß Ł ºŁ, Ł
ª º f , º Œ Ø Œ æ Ł.
˜ Œ º æ . ˇ æ ![]() Œ Ł æŒ º Ł
Œ Ł æŒ º Ł
ª º f . ª 6.5.2
![]() ª (∀ 1 6 i
6 t
) Pi
- g.
ª (∀ 1 6 i
6 t
) Pi
- g.
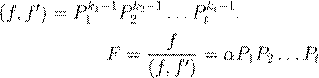 æ Ł
æ Ł
.
![]()
| 6.6 ºª Æ Ł |
æŒŁ Œ ß |
º |
|
| ˇ æ k æ |
º . |
||
| ¯˛—¯ 6.6.1 ( |
æŁº ßı æº |
Ł ı, º øŁı º- |
|
| ª Æ Ł æŒŁ Œ |
º ). ˛ æŁ |
º ŁŒæŁ |
ª æ- |
| ª º k æ |
ºŁ ß æº øŁ |
æŁº ß |
Ł . |
| 1) º Æ Ø ª º |
f º Ł º Ø æ |
Ł æ Œ Ł Ł |
Ł Ł |
| º k , Ł |
º k , Œ Ø Ø |
, Ł Œ ; |
|
| 2) Ł Ł ß Ł æ Ł; |
º k º æ |
ª º ß º Œ |
Ø |
| 3) ª º º ºŁ; |
k æ æ º |
k ºŁ Ø ß |
Ł- |
| 4) º Æ Ø ª º |
f º Ł º Ø æ |
Ł æ Œ Ł Ł |
Ł Ł |
| º k Ł |
º k æ º Œ Œ Ø æ Łı Œ |
æ Ø, |
|
Œ Œ æ ª º f .
˜ Œ º æ . 1) ⇒ 2)
ˇ æ f º Æ Ø ª º , degf > 2. ª æº Ł 1)
ª º Ł º k Œ Ø Ł Œ γ . ª -
º Ł 6.4.1 f = (x −γ )g . º º f º æ Ł Ł ß k .
6.6. ºª Æ Ł æŒŁ Œ ß º
2) ⇒ 3)
| ˇ æ f ª º º Ł º Ø æ Ł. ª 6.4.2 ª æ Ł Ł f = αP 1 · P 2 · ... · Ps , ª α ∈ k ∗ , Pi Ł ß Ł Ł ß k ª º ß. ¨ æº Ł 2) æº , Pi = x − γi ⇒ f = α (x − γ 1 )(x − γ 2 )... (x − γn ). ŒŁ Æ |
|
| ª º æ æ ºŁ Ø ß Ł ºŁ. 3) ⇒ 4) |
|
| ¨ f = α (x − γ 1 )(x − γ 2 )... (x − γs ). ˛Æœ Ł Œ ßı Ł º Ø æ Ł. |
Ł Ł Ł Ł |
| f = (x − γ 1 )k 1 (x − γ 2 )k 2 ... (x − γt )k t , |
ki ∈ N. |
| ´Ł , γ 1 ,...,γt Œ Ł ª º f æ Œ |
æ Ł k 1 ,...,kt Ł |
| degf = k 1 +... +kt . ŒŁ Æ Łæº Œ Ø Łı Œ æ Ø æ Ł ª º f . 4) ⇒ 1) |
ª º f æ |
| ˇ æ ª º f Ł deg > 0 . ª æº |
Ł 4) k 1 +k 2 +... + |
| + kt = degf > 1 ⇒ (∃ 1 6 i 6 t ) ki > 1. ˙ Ł , |
ª º f Ł |
Œ Ø Ø Œ γi
. ![]()
˛ º Ł 6.6.1. ˇ º k ß æ ºª Æ Ł æŒŁ Œ ß , æºŁ º º Æ Ł æŁº ßı æº ŁØ ß 6.6.1.
˙ Ł 6.6.1. ˇ º Q Ł R º æ ºª Æ Ł æŒŁ Œ ß Ł, Œ Œ Œ ß º æ 1) æº Ł ß 6.6.1. ˇ Ł æº -
Ł ª º f = x 2 + 1 . ˛ Ł Ł ª Œ Ł º Q,
Ł º R.
˛ º Ł 6.6.2. ºª Æ Ł æŒŁ ߌ Ł º k ß æ Ł ł ºª Æ Ł æŒŁ Œ æłŁ Ł º k .
˛ º Ł 6.6.3. ˇ º k
![]() ß æ ºª Æ Ł æŒŁ ߌ Ł º k
, æºŁ ß º ß æº øŁ 3 æº Ł :
ß æ ºª Æ Ł æŒŁ ߌ Ł º k
, æºŁ ß º ß æº øŁ 3 æº Ł :
| 2. k º æ ºª Æ Ł æŒŁ Œ ß º ; |
|
| 3. æºŁ k ⊂ k 0 ⊂ k Ł k 0 ºª Æ Ł æŒŁ Œ º , |
k 0 = k . |
| ¯˛—¯ 6.6.2 ( æ ºª Æ ß). ˇ º Œ Łæ º C º æ ºª Æ Ł æŒŁ Œ ß º . |
º Œæ ßı |
| º æ Ł 6.6.2.1. ºª Æ Ł æŒŁ ߌ Ł º Øæ Łæ º R º æ º Œ º Œæ ßı Łæ º, æ R = C. |
Ł º ßı |
| ˜ Œ º æ . ˜ Øæ Ł º , æ R ºª Æ Ł æŒ |
ߌ Ł |
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]() º R. ª R ⊂ R. ˜ º , ª º x
2
+1
Ł Œ R, æ i
∈ R. ß º æ ª Ł º Œ ª , Œ ª (∀ x,y
∈ R) x
+ +yi
∈ R, æ C ⊂ R. ¨ R ⊂ C ⊂ R. ˇ 6.6.2 C º æ ºª Æ Ł æŒŁ Œ ß , ª º Ł 6.6.3 Ł C = R.
º R. ª R ⊂ R. ˜ º , ª º x
2
+1
Ł Œ R, æ i
∈ R. ß º æ ª Ł º Œ ª , Œ ª (∀ x,y
∈ R) x
+ +yi
∈ R, æ C ⊂ R. ¨ R ⊂ C ⊂ R. ˇ 6.6.2 C º æ ºª Æ Ł æŒŁ Œ ß , ª º Ł 6.6.3 Ł C = R.
ˇ æ γ 1 ,γ 2 ,...,γn º ß º k .
˛ º Ł 6.6.4. º ß Ł æŁ Ł æŒŁ Ł ª º Ł º γ 1,...,γ n ß æ æ ß Ł :
σ 1 = γ 1 + γ 2 + ... + γn ;
σ 2 = γ 1 γ 2 + γ 1 γ 3 + ... + γ 1 γn + γ 2 γ 3 + ... + γ 2 γn + ... + γn −1 γn ;
...
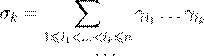 ;
;
σn = γ 1 ...γn .
ˇ º Ł 6.6.1. ¯æºŁ γ 1 ,γ 2 ,...,γn ∈ k ,
f (x ) = (x +γ 1 )(x +γ 2 )... (x +γn ) = xn +σ 1 xn −1 +... +σk xn −k +... +σn ,
ª σ 1 ,σ 2 ,...,σn º ß æŁ Ł æŒŁ ª º ß
γ 1 ,γ 2 ,...,γn .
6.6. ºª Æ Ł æŒŁ Œ ß º
˜ Œ º æ . Æß æ Ł Œ , æ -
Ł æŒ ÆŒŁ æ øŁ æº Ł Ł æ Ł Æ ß æº ª ß . ![]()
º æ Ł . ¯æºŁ γ 1 ,γ 2 ,...,γn ∈ k , f (x ) = (x − γ 1 )(x − γ 2 )... (x −
− γ n ) = x n − σ 1x n −1 + σ 2x n −2 − ... + (−1)k σ k x n −k + ... + (−1)n σ n ,
ª σ 1 ,σ 2 ,...,σn º ß æŁ Ł æŒŁ ª º ß
γ 1 ,γ 2 ,...,γn .
| ˜ Œ |
º æ |
. ´ æ |
º , æ º |
ŁŁ 6.6.1 |
æ |
|
| γi |
æ |
Ł |
−γi . ª |
σk Ł æ (−1)k σk Ł |
æ ß æº |
æ Ł |
Æ æ º . ![]()
| ¯˛—¯ 6.6.3 ( |
´Ł |
). ˇ æ |
f (x ) = xn + α 1 xn −1 + |
| + α 2 xn −2 + ... + αn Ł |
ª |
º Ł |
ºª Æ Ł æŒ ß- |
![]()
Œ ŁŁ k Œ Ł γ 1 ,γ 2 ,...,γn . ª σk = (−1)k αk , ª σ 1 ,σ 2 ,...,σn
º ß æŁ Ł æŒŁ ª º ß Œ Ø γ 1 ,γ 1 ,...,γn .
˜ Œ º æ . ˝ º k
![]() ª º
ª º
f (x ) = (x − γ 1 )(x − γ 2 )... (x − γn ),
ª γ 1 ,γ 2 ,...,γn Œ Ł f (x ) k . ˇ æº æ Ł Ł º Ł 6.6.1
Ł :
f (x ) = xn − σ 1 xn −1 + σ 2 xn −2 − ... + (−1)k σk xn −k + ... + (−1)n σn .
ª Ø æ ß, æº Ł f (x ) = xn +α 1 xn −1 +... +αn . ŒŁ Æ -
Ł ß Ł ª Ł ª ª º Æß øŁ æ x . ª , Œ Ł Ł ß Ł Ł Œ ßı æ ı x º ß æ . ¨ −σ 1 = α 1 , σ 2 = α 2 ,..., (−1)k σk = αk ,..., (−1)n σn =
= αn . ¨ (∀ 1 6 k 6 n ) (−1)k σk = αk . Ł (−1)k , º Ł
σk = (−1)k αk .
32
![]() æ ßØ æº Ø ß 6.6.3:
æ ßØ æº Ø ß 6.6.3:
n=2, f (x ) = x 2 + px + q . ˇ æ x 1 , x 2 Œ Ł f (x ), ª
( σ 1 = x 1 + x 2 = −p ; σ 2 = x 1 · x 2 = q.
n=3, f (x ) = x 3 + px 2 + qx + r . ˇ æ x 1 , x 2 x 3 Œ Ł f (x ), ª
σ 1 = x 1 + x 2 + x 3 = −p ; σ 2 = x 1 x 2 + x 1 x 3 + x 2 x 3 = q ; .
σ 3 = x 1x 2x 3 = −r
6.7 ª º ß Łæº ß Ł º Ł
— ææ Ł æº Ø, Œ ª k = C. ˇ æ Ø ºª Æ ß, º
C º æ ºª Æ Ł æŒŁ Œ ß , ª º ß º
C ƺ º Æß Ł æŁº ßı æº ŁØ ß 6.6.1. ´ æ æ Ł, Ł Ł ß Ł º C º æ ª º ß º Œ Ø æ Ł. ˜ º , º Æ Ø ª º º Ł º Ø æ Ł º C Ł , Œ Ø , Ł Œ . ˝ Œ , Œ Ł æŒ º Ł º Æ ª ª º f º Ł º Ø æ Ł º C Ł Ł :
f (x ) = α (x − γ 1 )k 1 (x − γ 2 )k 2 ... (x − γt )k t ,
ª γ 1 ,γ 2 ,...,γt ∈ C.
— ææ Ł æº Ø, Œ ª k = R. ˇ æ γ = α +βi , ª α,β ∈ R, β 6=
6= 0 . ´ æº ª , γ æ ø æ Œ º Œæ Łæº .
ˇ º Ł 6.7.1. ¯æºŁ γ æ ø æ Œ º Œæ Łæº ,
![]() ª º (x
−γ
)(x
−γ
) º æ Œ ß ı º æ Øæ Łº ß Ł Œ Ł Ł Ł Ł Ł º ß ŁæŒ Ł Ł .
ª º (x
−γ
)(x
−γ
) º æ Œ ß ı º æ Øæ Łº ß Ł Œ Ł Ł Ł Ł Ł º ß ŁæŒ Ł Ł .
˜ Œ º æ . ˜ Øæ Ł º , (x − γ )(x − γ ¯) = x 2 − (γ + ¯γ )x + γγ ¯ =
= x 2 −2αx +α 2 +β 2 ∈ R[x ], ª D = (−2α )2 −4(α 2 +β 2 ) = −4β 2 < 0,
Œ Œ Œ γ æ ø æ Œ º Œæ Łæº .
6.7. ª º ß Łæº ß Ł º Ł
¯˛—¯ 6.7.1. ¯æºŁ æ ø æ Œ º Œæ Łæº γ º æ
Œ ª º f æ Øæ Ł º ß Ł Œ Ł Ł Ł, Œ -
º Œæ æ Łæº γ ¯ Œ º æ Œ ª ª º Ł Ł Ø Œ æ Ł, Ł Œ γ .
˜ Œ º æ . ˇ æ f (x ) = αn xn + ... + α 1 x + α 0 , ª αi ∈ R Ł γ æ ø æ Œ º Œæ ßØ Œ f (x ), æ f (γ ) = 0.
αn γn + ... + α 1 γ + α 0 = 0.
ˇ Ø Œ Œ º Œæ æ ß Łæº , º Ł
![]()
αn γn + ... + α 1 γ + α 0 = 0.
´ æ º æ æ Øæ Ł Œ º Œæ æ ßı Łæ º, Ł
α ¯n · γ ¯n + ... + ¯α 1 · γ ¯ + ¯α 0 = ¯0.
Œ Œ Œ αi Ł 0 ∈ R, α ¯i = αi , ¯0 = 0. ˇ º
αn (¯γ )n + ... + α 1 γ ¯ + α 0 = 0.
æ Œ ß , f (¯γ ) = 0 æ γ ¯ º æ Œ
ª º f (x ) . ˇ Œ , Œ æ Œ γ ¯ æ æ Œ æ Œ γ . ˇ æ Œ æ γ k , Œ æ γ ¯ l . ˝ Æı Ł Œ , k = l . ˜ æ Ł Ł , æ k 6= l . ˇ æ ,
Ł , k > l , ª f = (x − γ )k (x − γ ¯)l g (x ), ª g (γ ) 6= 0,g (¯γ ) = 06.
ª f (x ) = [(x − γ )(x − γ ¯)]l (x − γ )k −l g (x ) = [(x − γ )(x − γ ¯)]l g 1 (x ),
æ![]() . ˇ º Ł (x
− γ
)(x
− γ
¯) ∈ R[x
],
. ˇ º Ł (x
− γ
)(x
− γ
¯) ∈ R[x
],
![]() .
.
´Ł , g 1 (x ) = (x − γ )k −l g (x ) Ł γ æ Ł Œ º Ł º Ø
Œ æ Ł, k − l > 0, Ł æ Ł Œ γ ¯. Ł Ł
Ł Œ ß Ø Ø. º ªŁ Ł Ł Œ Ł Ł º Ł , l > k .
34
º æ Ł 6.7.1.1. ø æ Œ º Œæ ß Œ Ł ª º æ Øæ Ł º ß Ł Œ Ł Ł Ł Œ º Œæ æ ß.
¯˛—¯ 6.7.2 ( Ł Ł ßı ª º ı R). ˝ -
º Øæ Ł º ßı Łæ º R Ł Ł ß Ł º æ ª º ß
Ø æ Ł Ł Ł º Œ Œ ß ı º ß, ŁæŒ Ł ŁŒ ßı Ł º ßØ.
˜ Œ º æ . ˇ æ f (x ) ∈ R[x ] Ł degf (x ) > 3. ª º
![]() Ł ºª Æ Ł æŒ ßŒ ŁŁ R = C Ł Œ Ø Ł
Ł ºª Æ Ł æŒ ßŒ ŁŁ R = C Ł Œ Ø Ł
Œ α . ¯æºŁ α ∈ R , f (x ) = (x − α )g (x ), ª g (x ) ∈ R[x ] æ
ª º f Ł Ł R. ¯æºŁ α æ ø æ Œ º Œæ Łæº , α ¯ Œ Æ Œ ª º f . ˇ º Ł
f (x ) = (x − α )(x − α ¯)g (x ) = (x 2 − 2Reα · x + |α |2 )g (x ).
´ æº
![]() .
.
´Ł , f (x ) æ Ł Ł R. ŒŁ Æ , º Æ Ø ª º f , æ Œ ª degf > 3, º æ Ł Ł ß R.
ˇ æ f = ax 2 +bx +c,a 6= 0. ¨ æ , Œ ßØ ı º æ æ ºŁ Ø ß Ł ºŁ f = a (x −x 1 )(x −x 2 ) R ª Ł
º Œ ª , Œ ª ª ŁæŒ Ł Ł D > 0. ´ æº , ª º
f
Ł Ł R. º º , Æ Ł Ł R ª Ł º Œ ª , Œ ª D
= b
2
− 4ac <
0. ª º ß Ø æ Ł º æ Ł Ł ß Ł º Æß º . ![]()
º æ Ł 6.7.2.1. ¸ Æ Ø ª º º Ł º Ø æ Ł º Øæ Ł º ßı Łæ º Ł Œ Ł æŒ æ º Ł Ł :
f = α (x − γ 1 )k 1 ... (x − γt )k t (x 2 + β 1 x + δ 1 )l 1 ... (x 2 + βr x + δr )l r ,
![]()
![]() ª α,βi
,δi
,γj
∈ R, βi
2
− 4δi
<
0, kj
,li
∈ N Ł i
= 1,r, j
= 1,t
.
ª α,βi
,δi
,γj
∈ R, βi
2
− 4δi
<
0, kj
,li
∈ N Ł i
= 1,r, j
= 1,t
.
6.7. ª º ß Łæº ß Ł º Ł
º æ Ł 6.7.2.2. ¸ Æ Ø ª º æ Øæ Ł º ß Ł Œ Ł Ł -
Ł Ø æ Ł Ł , Œ Ø , Ł Øæ Ł º ßØ Œ .
˜ Œ º æ . ´ æ º , æº æ Ł 6.7.2.1 degf = k 1 + ... + +kt +2l 1 +... +2lr . ˇ æº Ł æ f Łæº , æº º k 1 + ... + kt Łæº , Ł (∃ 1 6 i 6 t ) ki > 1, æ γi
º æ Øæ Ł º ß Œ ª º f
. ![]()
ˆº 7
˛æ ß ºª Æ Ł æŒŁ æ Œ ß
36
ˆº 8
¸Ł Ø ß æ æ
8.1 ˇ Ł ºŁ Ø ª æ æ
˛ º Ł 8.1.1. ˇ æ k Ł V Ł º ßı æ . ˆ -
, æ V º ł ºª Æ Ł æŒ Ł æ æ º Ł ºŁŒ k , æºŁ Æ Ł Œ ª Ł Ł k × V → V . ˇ Ł Æ ŁŁ, Æ -
ßØ ß (α,a ), ª α ∈ k, a ∈ V ß æ Ł Ł α a Ł Æ æ αa .
˙ Ł 8.1.1. ºª Æ Ł æŒŁ ŁŁ, Ł ß æ V , ß æ Ł Ł ºª Æ Ł æŒŁ Ł Ł Ł. ´ Œ æ æ k ø æ ª Æ ßæ º , Œ Æ ßæ ß . º ß º k Æ Æ α,β,γ,α 1 ,α 2 ,...
˛ º Ł 8.1.2. ¸Ł Ø ß ( Œ ß ) æ æ º
k ß æ æ V , ææ æ æ º Ø
Ø ºª Æ Ł æŒ Ø Ł Ø æº Ł Ł ł Ø ºª Æ Ł æŒ Ø Ł Ø Ł æŒ º ß º k , º ß Ł æº øŁ æ Ł ŒæŁ .
1. a + b = b + a ;
2. a + (b + c ) = (a + b ) + c ;
37
3. (∀ a,b ∈ V ) (∃ x ∈ V ) b + x = a ;
4. α (a + b ) = αa + αb ;
5. (α + β )a = αa + βa ;
6. (αβ )a = α (βa ) = β (αa );
7. 1 · a = a ,
ª a,b,c,x ∈ V ; α,β, 1 ∈ k .
˙ Ł 8.1.2. æ V æ ß Æ Łæ ß æ
ºŁ Ø ª æ æ . ¯ª º ß Æ Æ a,b,c,a 1 ,a 2 ,...
Ł ß Œ Ł.
Øæ ºŁ Ø ßı æ æ
1. (∀ a ∈ V ) (∃ 0 ∈ V ) a + 0 = a ;
2. (∀ a ∈ V ) (∃ (−a ) ∈ V ) a + (−a ) = 0;
3. (∀ a,b ∈ V ) (∃ (a − b ) ∈ V ) a − b = a + (−b );
4. αa = 0 ⇔ α = 0 ŁºŁ a = 0;
5. α (−a ) = (−α )a = −αa ;
6. α (a − b ) = αa − αb ;
7. (α − β )a = αa − βa .
˜ Œ º æ . ŒæŁ ß 1 3 ºŁ Ø ª æ æ Œ ß , (V, +) Æ Ł Ł ª , æ ºŁ ß æ Øæ 1) 3).
4) ˝ Æı Ł æ .
¨ αa = (α + 0)a = αa + 0a ⇒ 0a = αa − αa = 0. ˇ º ,
0a = 0.
8.2. ` Łæ ºŁ Ø ª æ æ
¨ αa = α (a + 0) = αa + α 0 ⇒ α 0 = αa − αa = 0. ˇ º ,
α 0 = 0.
˜ æ æ .
ˇ æ αa = 0 . ¯æºŁ α = 0 , æ Œ . ¯æºŁ α 6= 0 Æ æ ø -
æ α −1 ∈ k . ª a = 1 · a = (α −1 α )a = α −1 (αa ) = α −1 · 0 = 0.
5) — æ Ł αa + α (−a ) = α (a + (−a )) = α · 0 = 0 ⇒ α (−a ) = −αa .
˜ º , αa + (−α )a = (α + (−α ))a = 0 · a = 0 ⇒ (−α )a = −αa .
6) ¨ , α (a − b ) = α (a + (−b )) = αa + α (−b ) = αa − αb .
7) ˇ æ Ł (α
− β
)a
= (α
+ (−β
))a
= αa
+ (−β
)a
= αa
− βa
. ![]()
| ˇ Ł ß ºŁ Ø ßı æ æ : |
|||
| 1. V = {0} º ºŁ Ø |
æ |
æ ( Ł Ł º |
). |
| 2. V = kn = {(α 1 ,...,αn )|αi ∈ k } æ º k . |
Π|
Ł ºŁ Ø |
æ - |
| 3. V = M (m ×n,k ) Ł ß |
æ Ł m ×n æ º |
Ł Ł k . |
|
| 4. V = L æ ł ŁØ ŁØ. |
Ø æŁæ ß ºŁ |
Ø ßı - |
|
| 5. V = k [x ] æ ª º Ł Ł Ł Ł k . 6. V = {f (x ) ∈ k [x ]|deg f 6 n }. |
ª Ł æ |
ª æ Œ - |
|
| 8.2 ˚ ß Ł Æ æŒ |
ß |
ºŁ Ø ß |
|
| æ æ . ` Łæ ºŁ |
Ø ª æ |
æ |
|
| ¸ ªŒ Ł , æ ß Ł |
Ł Œ ß, º |
ß Œ - |
|
| Ł ºŁ Ø æ æ |
æ æ Ææ Œ |
ß ºŁ Ø ß |
|
æ æ . æ , Ł Ł Ł Œ ß Łæ º ºŁ
º Œ æ Øæ ŁØ Œ Ł, Łæ º ºŁ Ł
æ Łı Œ . Œ Œ Ł Ł º Ł 8.1.2, ŁŁ Ææ Œ ºŁ Ø æ æ ƺ Ł æ ß Ł æ Øæ Ł, Ł
ŁŁ Œ Ł ºŁ Ø æ æ . ˇ , Ææ Œ ßı ºŁ Ø ßı æ æ ı ª Ł ºŁ Ø Ø Œ ÆŁ ŁŁ Œ , ºŁ Ø ŁæŁ ßı Ł ºŁ Ø ŁæŁ ßı æŁæ ı Œ , Œ Ł ŁŁ Ł æ Øæ ı ºŁ Ø Ø ŁæŁ æ Ł, Æ æ Ø
ºŁ Ø Ø ŁæŁ æ Ł, ºŁ Ø ß ŁŁ Ø æŁæ ß Œ -
ª , Æ Œ Ł º ßı æŁæ ı Œ , Æ Łæ Ł ª æŁæ ß Œ . ˝ æ Ł ºŁ Ł .
ˇ Ł : V = k [x ] . — ææ Ł æº ø æŁæ Œ :
1,x,x 2 ,...,xn ∈ V . æŁæ Œ º æ ºŁ Ø ŁæŁØ. ˜ Øæ Ł º ,
α 0 · 1 + α 1 x + α 2 x 2 + ... + αn xn = 0 ⇔ α 0 = α 1 = α 2 = ... = αn = 0,
Ł , 1,x,x 2,...,x n º æ ºŁ Ø ŁæŁ Ø æŁæ -
Ø Œ . ł æ , n Æ º Æß Ł Œ Œ ª Æ º łŁ . ˇ æ æ V æ ø æ ºŁ Ø ŁæŁ ß æŁæ ß Œ æ Œ ŒŁ ª Æ º łŁ Łæº Łı Œ .
˛ º Ł 8.2.1. ¸Ł Ø æ æ V ß æ Œ ß , æºŁ æ ø æ º Łæº N Œ , Łæº ºŁ Ø
ŁæŁ ßı Œ º Æ Ø æŁæ æ æ V æı Ł N . ´ Ł æº , ºŁ Ø æ æ V ß æ Æ æŒ ß .
ˇ Ł :
1. V = k n Œ ºŁ Ø æ æ .
2. V = k [x ] Æ æŒ ºŁ Ø æ æ .
8.2. ` Łæ ºŁ Ø ª æ æ
´ Œ ßı ºŁ Ø ßı æ æ ı ª Ł Æ Łæ
Œ Œ Œ Ø, Œ Ł Æ æŒ Ø æŁæ ß Œ . ´ æ æ Ł,
ª Ł Æ Łæ æ ª Œ ª ºŁ Ø ª æ æ V .
| ˛ º Ł 8.2.2. ` Łæ |
º ª Œ |
ª |
æ æ |
|
| V ß æ ºŁ |
Ø ŁæŁ |
æŁæ |
Π|
|
| B = {e 1 ,e 2 ,...,en }, º æº ŁØ: |
º Æ Ł æº |
øŁı |
æŁº |
ßı |
| 1. º Æ Ø Œ a ∈ V ºŁ Ø |
ß æ |
æŁæ |
B ; |
|
| 2. ∀ a ∈ V æŁæ (B,a ) |
º æ ºŁ Ø |
ŁæŁ Ø; |
||
| 3. æ æ V æ ø æ |
ºŁ Ø |
ŁæŁ ßı |
æŁæ |
æ |
| Łæº Œ Æ º łŁ , |
B . |
˛ º Ł 8.2.3. — æ º ª ºŁ Ø ª æ æ æ Ł æ Łæº 0. — æ º ª Œ ª ºŁ Ø ª æ æ V ß æ Łæº Œ º Æ Æ Łæ ª -
æ æ ŁºŁ ŒæŁ º Łæº ºŁ Ø ŁæŁ ßı Œ ª æ æ V .
— æ Œ ª ºŁ Ø ª æ æ V Æ Æ dim V ŁºŁ rang V .
ˇ Ł :
1. dim {0} = 0;
2. dim kn = n ;
3. dim M (m × n,k ) = mn ;
4. dim L = n − r ;
5. dim {f (x ) ∈ k [x ]|deg f (x ) 6 n } = n + 1.
ˇ æ V Œ ºŁ Ø æ æ Ł e 1 ,e 2 ,...,en ª Æ Łæ. ª º Æ Ø Œ a ∈ V ß Ł Æ Łæ
a = α 1 e 1 + α 2 e 2 + ... + αn en . (8.1)
Œ Œ Œ Æ Łæ º æ ºŁ Ø ŁæŁ Ø æŁæ Ø Œ , ß Ł (8.1) º Œ a Ł æ . ŒŁ Æ , Œ -
Œ a ∈ V æ Ł æ æ æ Ł æŁæ
(α 1 ,α 2 ,...,αn ) æŁ º Æ Łæ e 1 ,e 2 ,...,en .
˛ º Ł 8.2.4. ˚ Ł Ł (Œ Ł) Œ a ∈ V æŁ º ª Æ Łæ e 1 ,e 2 ,...,en ºŁ Ø ª æ æ V ß æ æ Œ æ Œ Ł Ł ºŁ Ø ª ß Ł Œ a Æ Łæ.
ˇŁł , Œ a = (α 1 ,α 2 ,...,αn ).
| ˛ |
º Ł 8.2.5. ˚ Ł |
ß |
æ ºÆ Œ a æŁ º |
|
| ª |
Æ Łæ e 1 ,e 2 ,...,en |
ß |
æ æ ºÆ , æ æ º ßØ Ł Œ - |
|
| Ł |
Œ a æŁ º |
ª |
Æ Łæ . |
|
| ˛Æ |
α 1 α 2 Ł a ˇ = . ... αn |
|||
| ˛ |
º |
Ł 8.2.6. æ |
º Ł |
Œ a ∈ V ª Œ Ł - |
| ª æ |
ºÆ |
æŁ º |
ª Æ |
Łæ æ æ V ß æ |
| æ |
ß Æ Ł ºŁ |
Ø ª |
æ æ V æ Ł n |
|
| Π|
Ł |
ºŁ Ø æ |
æ |
k n . |
| æ |
, |
Œ ßØ Æ Łæ e 1 ,e 2 ,...,en º æ æ |
||
Æ Ł V → kn .
8.3. ¨ Ł ºŁ Ø ßı æ æ
ˇ º Ł 8.2.1. ˚ Ł ßØ æ ºÆ æ ß ı Œ æ Œ Ł ßı æ ºÆ æº ª ßı Œ . ˚ Ł ßØ æ ºÆ Ł Ł Œ æŒ º , Œ Ł æ ºÆ-
ª Œ , æŒ º .
º Ł 8.2.1 , a +ˇ b = a ˇ +ˇb Ł αa ˇ = αa ˇ.
˜ Ł ª ŁæŁ (8.1). æ , a ˇ> = (α 1 ,α 2 ,...,αn )
Ł æ Ł 1×n . — ææ Ł Æ Łæ ßØ æ ºÆ æ æ
![]() Ł æ Ł n
×1. ª a
ˇ>
e
˜ = α
1
e
1
+α
2
e
2
+
Ł æ Ł n
×1. ª a
ˇ>
e
˜ = α
1
e
1
+α
2
e
2
+
. ŒŁ Æ , a = a ˇ> e ˜ Ł Łæ æ
8.3 ¨ Ł ºŁ Ø ßı æ æ
ˇ æ V Ł V 0 ºŁ Ø ßı æ æ Ł Ł æ ß º k .
˛ º Ł 8.3.1. ¨ Ł ºŁ Ø ª æ æ V ºŁ-
Ø æ æ V 0 Ł Ł æ ß º k ß æ æ Œ ÆŁ Œ Ł f : V → V 0 , º ø æº Ł ºŁ Ø æ Ł:
1. (∀ a,b ∈ V ) f (a + b ) = f (a ) + f (b );
2. (∀ α ∈ k, a ∈ V ) f (αa ) = αf (a ).
æº Ł 1 , Æ Ł f º æ Ł Ł -
Ł Ł Ø ª ß (V,
+)
Ł Ł ª ![]() .
.
˛ º Ł 8.3.2. ¸Ł Ø æ æ V ß æ Ł ß ºŁ Ø æ æ V 0 (V ∼ = V 0 ), æºŁ æ ø æ ı Æß
Ł Ł Ł f : V → V 0 .
ˇ º Ł 8.3.1. ˛ ł Ł Ł Ł º æ ł Ł
Œ Ł º æ Ł Œº ææ ºŁ Ø ßı æ æ Ł Ł æ ß º k .
º Ł 8.3.1 , º ł Ł Ł æ Ł
| æ ºŁ ß æº |
øŁ |
Ł |
||
| 1. V ∼ = V , æ |
ß º æ |
æ Øæ |
º ŒæŁ |
æ Ł; |
| 2. æºŁ V ∼= V 0, |
V 0 ∼= V (æŁ |
Ł |
æ |
); |
3. æºŁ V 00 ∼= V 0 Ł V 0 ∼= V , V 00 ∼= V ( Ł Ł æ ).
¯˛—¯ 8.3.1 ( æ Øæ ı Ł ßı ºŁ Ø ßı æ æ ). ºŁ ß æº øŁ Ł :
1. Ł Ł Ł ºŁ Ø ŁæŁ Ø æŁæ ß Œ ı
ºŁ Ø ŁæŁ ß , ºŁ Ø ŁæŁ ß æŁæ ß Œ
| ı |
ºŁ Ø |
ŁæŁ ß ; |
||||
| 2. Ł |
ß |
ºŁ Ø ß |
æ æ |
ºŁÆ |
Π|
- |
| ß , ºŁÆ |
Æ æŒ |
ß ; |
3. Ł Ł Ł Æ Łæ æŁæ ß Œ ı Ł Æ Łæ, ª æŁæ ß Œ Ł Ł Ł Ł æ .
˜ Œ º æ . 1) ˇ æ f : V → V 0 º æ Ł Ł . ´ -
ºŁ Ø ŁæŁ æŁæ Œ a 1 ,a 2 ,...,as Ł V . , æ ø æ æŒ º ß α 1 ,α 2 ,...,αs æ ß º ŒŁ , α 1 a 1 + α 2 a 2 + ... + αs as = 0. ˇ Ø Œ Æ Łı Œ -
f (α 1 a 1 + α 2 a 2 + ... + αs as ) = f (0). Œ Œ Œ f Ł Ł ,
α 1 f (a 1 ) + α 2 f (a 2 ) + ... + αs f (as ) = 0, æ æ αi = 0. ˇ æº æ ł Ł Œ ß , Œ ß f (a 1 ),f (a 2 ),...,f (as ) º æ ºŁ Ø ŁæŁ ß Ł V 0 .
8.3. ¨ Ł ºŁ Ø ßı æ æ ˇ æ a 1 ,a 2 ,...,as ºŁ Ø ŁæŁ æŁæ Œ Ł V . ˝
Œ , f (a 1 ),f (a 2 ),...,f (as ) Œ º æ ºŁ Ø ŁæŁ-
Ø. ˜ æ Ł Ł , æ æŁæ f (a 1 ),f (a 2 ),...,f (as ) º æ ºŁ Ø ŁæŁ Ø. ª ææ Ł Æ Ł f −1 : V 0 → V ,
Œ Œ º æ Ł Ł . ˇ Ł Æ ŁŁ ºŁ Ø-
ŁæŁ ß Œ ß f (a 1 ),f (a 2 ),...,f (as ) Ø ºŁ Ø ŁæŁß Œ ß a 1 ,a 2 ,...,as , Ł Ł ºŁ Ø Ø ŁæŁ æ Ł
a 1 ,a 2 ,...,as .
2) ˇ æ f : V → V 0 Ł V º æ Œ ß ºŁ Ø ß æ æ . , æ ø æ º Łæº N Œ ,
| Łæº |
Œ º Æ Ø ºŁ Ø ŁæŁ Ø æŁæ ß Ł |
æ - |
| æ V |
æı Ł ª Łæº N . Œ Œ Œ Ł Ł Ł |
º Œ |
| ºŁ Ø |
ŁæŁ æŁæ Œ ı Ł ºŁ Ø |
Ł- |
| æŁ , |
æ æ V 0 Łæº Œ º Æ Ø ºŁ Ø |
Ł- |
| æŁ Ø æŁæ |
Œ Æ ª Ł Ł Łæº N , æº |
º |
| æ æ |
V 0 Æ Œ ß . |
|
| ˇ æ V |
º æ Æ æŒ ß ºŁ Ø ß æ æ |
. ˝ |
Œ , Ł V 0 æº Œ Æ Æ æŒ ß . ˜ æ Ł Ł , æ V 0 º æ Œ ß ºŁ Ø ß -
æ æ . ª ææ Ł Ł Ł f −1 : V 0 → V . ˇ Ł
Ł Ł Ł Œ æ Ł V 0 Æ æº Œ æ
V , Ł Ł æº Ł .
3) ˇ æ A æŁæ Œ Ł V , B Æ Łæ æŁæ ß Œ A Ł
f : V → V 0 Ł Ł . ª , Œ Œ Œ B ⊂ A , f (B ) ⊂ f (A ). ˜ º ,
A ºŁ Ø ß æ B , ª f (A ) Æ ºŁ Ø ß æ f (B ) . ˝ Œ , Œ Œ Œ B ºŁ Ø ŁæŁ æŁæ Œ -
, f (B ) Œ º æ ºŁ Ø ŁæŁ Ø. ŒŁ Æ , f (B ) º æ Æ Łæ f (A ) , æ Æ Łæ B æŁæ ß Œ A ı Ł
Æ Łæ f
(B
)
æŁæ ß Œ f
(A
)
. ΠΠΠf
º æ ÆŁ Œ Ł Ø, Łæº Œ B
Łæº Œ f
(B
), æ r
(A
) = r
(f
(A
)). ![]()
º æ Ł 8.3.1.1. ¨ ß Œ ß ºŁ Ø ß æ æ
Ł Ł Œ æ .
˜ Œ º æ . ˜ Øæ Ł º , f : V → V 0 Ł Ł Ł V Ł V 0 º æ Œ ß Ł ºŁ Ø ß Ł æ æ Ł. ª Æ Łæ
e
1
,e
2
,...,en
æ æ V
ı Ł Æ Łæ f
(e
1
),f
(e
2
),...,f
(en
) æ æ V
0
, æ dim V
= n
= dim V
0
. ![]()
| ¯˛—¯ 8.3.2. ¸ Æ Œ ºŁ Ø |
æ æ V |
||
| æ Ł n Ł |
Œ Ł ºŁ Ø |
æ æ kn |
|
| Ł Ł Ł Ł |
æ Łª æ æ ø |
æ |
ª Æ- |
| Ł f : V → kn |
æŁ º º Æ ª Æ Łæ |
æ |
æ V . |
| ˜ Œ º æ . ˇ æ |
e 1 e 2 dim V = n Ł e ˜ = ... en |
Æ |
Łæ V . — ææ - |
| Ł æ Æ |
Ł f : V → kn . ¨ æ |
, |
æºŁ a = a ˇ> e ˜, |
| f (a ) = a ˇ. ˇ Œ , |
Æ Ł f º |
æ |
Ł Ł . |
| ´ - ßı, f º æ a ˇ = ˇb ⇒ a = b . |
Ł œ Œ Ł Ø. ˜ Øæ Ł º |
, æºŁ f (a ) = f (b ), |
|
| ´ - ßı, f º æ æ œ Œ Ł Ø. ´ æ |
º , º Æ Ø |
||
æ ºÆ a ˇ ∈ kn Ł æ Ł Œ a = a ˇ> e ˜. ª f (a ) = a ˇ.
˛æ æ Œ , Æ Ł f æ ı ŁŁ. — ææ -
Ł f (a + b ) = a +ˇ b = a ˇ + ˇb = f (a ) + f (b ). f (αa ) = αa ˇ = αa ˇ = αf (a ).
ŒŁ Æ f : V → k n º æ Ł Ł , æº º
V
∼
= kn
. ![]()
º æ Ł 8.3.2.1. ˚ ß ºŁ Ø ß æ æ Ł Œ Ø æ Ł Ł ß.
8.4. ˇ ı ª Æ Łæ Œ ª . Ł ı
˜ Œ º æ . ˜ Øæ Ł º , æ æ dim V = n Ł dim V 0 = n . ª 8.3.2 V ∼ = kn Ł V 0 ∼ = kn , æº º -
V
∼
= V
0
. ![]()
| º æ Ł 8.3.2.2. — ª æŁæ ß Œ Œ |
ª ºŁ Ø |
ª |
|
| æ æ V ª æŁæ ß Œ Ł |
ßı æ |
ºÆ Œ |
|
| Ø æŁæ ß æŁ º º Æ ª Æ Łæ æ |
æ |
V . |
|
| ˜ Œ º æ . ˇ æ a 1 ,a 2 ,...,as æŁæ |
Π|
Ł V . — ææ |
- |
| Ł f : V → k n æ ßØ Ł Ł |
, ª |
æŁæ Œ |
- |
| a 1 ,a 2 ,...,as ı Ł a ˇ1 ,a ˇ2 ,...,a ˇs . ˝ |
Ł 3 |
- |
ß 8.3.1 r
(a
1,a
2,...,a
s
) = r
(a
ˇ1,a
ˇ2,...,a
ˇs
). ![]()
8.4 ˇ ı ª Æ Łæ Œ ª . Ł ı
ˇ æ V Œ ºŁ Ø æ æ k , dim V = n Ł æ
e 1 u 1
e 2 u 2 e = Ł u e = ... e ...
en un
Æ Łæ æ æ V . ´ß Ł Œ ß Æ Łæ u e Œ ß
![]() Łæ e
e:
Łæ e
e:
| u 1 = α 11e 1 + α 21e 2 + ... + α n 1e n ; |
|
| u 2 = α 12e 1 + α 22e 2 + ... + α n 2e n ; ... u n = α 1n e 1 + α 2n e 2 + ... + α nn e n . |
(8.2) |
˛ º Ł 8.4.1. Ł Ø ı Æ Łæ e e Œ Æ Łæ u e ß æ Ł , æ Ł Œ Ł , æ æ º Ø Ł Œ Ł-
Ł ºŁ Ø ª ß Ł Œ![]() Łæ u
e Œ ß Æ Łæ
Łæ u
e Œ ß Æ Łæ
| e . e |
||
| ˛ |
º Ł 8.4.1 , Ł ı > α 11 α 21 ... α n 1 α 11 α 12 ... α 1n α 12 α 22 ... α n 2 α 21 α 22 ... α 2n Q = = . ... ... ... ... ... ... ... ... α 1n α 2n ... α nn α n 1 α n 2 ... α nn |
|
| ˇ ß |
æ ºÆ Ł ß º æ Œ Ł ßØ æ ºÆ Œ |
u 1 . |
| ´ ß |
Œ Ł ßØ æ ºÆ Œ u 2 , Ł . . |
|
| ˛ |
º Ł 8.4.2. Ł Ø ı Æ Łæ e e Œ Æ Łæ |
u ß- e |
| æ |
Ł Q , æ ºÆ Ł Œ Ø º æ Œ Ł ß æ ºÆ ß |
|
| Π|
Æ Łæ u e æŁ º Æ Łæ e e , æ |
|
![]() .
.
| ˛ º Ł 8.4.3. Ł |
Ø |
ı |
Æ Łæ e e Œ Æ Łæ u e ß - |
||||||||||
| æ Ł Q , º æŁæ ß (8.2). |
æ |
u = Q > e e e |
Ł Łæ |
||||||||||
| ¯˛—¯ 8.4.1 ( Ł |
Ł |
ı |
). |
ºŁ ß æº øŁ |
|||||||||
| 1. Ł ı |
ª |
Æ Łæ |
Œ ª |
º æ æ - |
|||||||||
| Æ Ø. ˛Æ , º Æ |
æ Æ |
Ł |
ææ - |
||||||||||
| Ł Œ Œ Ł ª Æ Łæ . |
ı |
ª Æ |
Łæ Œ Œ |
||||||||||
| 2. Ł ß ı Æ |
Łæ |
e Œ Æ e |
Łæ u Ł e |
Æ Łæ u Œ Æ Łæ e e e |
|||||||||
| º æ Ł Æ |
ß Ł. |
||||||||||||
| ˜ Œ º æ . 1) ˇ æ Q º Æ |
æ Æ |
Ł Ł e e - |
|||||||||||
| ßØ Æ Łæ æ æ V . ˇ æ Ł |
Œ ß u 1 ,u 2 ,...,un ŒŁ |
||||||||||||
| 8.4. ˇ ı ª Æ |
Łæ Œ ª |
. Ł |
ı |
||||||||||
| Æ , Æß Łı Œ |
Ł ß æ |
ºÆ ß |
æŁ |
º |
Æ |
Łæ |
e æ e |
- |
|||||
| ºŁ æ æ ºÆ Ł |
Ł ß Q . |
||||||||||||
| ΠΠΠ|Q | 6= 0, |
æ ºÆ ß |
Ł ß Q |
º |
æ |
ºŁ |
Ø |
Ł- |
||||||
æŁ ß Ł, Ł Œ ß u 1,u 2,...,u n Æ ºŁ Ø ŁæŁ ß Ł.
´ æŁº ª , Œ ß u 1 ,u 2 ,...,un Œ æ Æ Łæ u e æ æ V .
ˇ æ Ł Æ Ł u e = Q > e e , æ Ł Q º æ Ł Ø ı ª Æ Łæ e e Œ æ Æ Łæ
u e .
2) ˇ æ ![]() Ł Æ Łæ æ æ V
. ˇ æ Q
Ł ı e
e
Πu
e
, R
Ł ı
Ł Æ Łæ æ æ V
. ˇ æ Q
Ł ı e
e
Πu
e
, R
Ł ı ![]() . ª º Ł 8.4.3 Æ
. ª º Ł 8.4.3 Æ
Ł u e = Q > e e , e e = R > u e . ˛ æ , e e = R > (Q > e e ) = (R > Q > )e e = (QR )> e e .
| æ Œ |
ß |
, |
Ł |
QR º æ |
Ł Ø |
||
| ı e e Œ e e . ˝ |
Ø |
Ł Ø |
º |
æ |
Ł E , æº |
º |
|
| QR = E . æ |
ł Ł |
Π|
ß |
, |
Q Ł R |
æ Æ |
ß |
Ł Æ ß Ł ß, æ Q
= R
−1
. ![]()
| ¯˛—¯ 8.4.2. ˚ |
Ł |
ßØ æ |
ºÆ |
Π|
æŁ º |
- |
| ª Æ Łæ Œ Ł |
æ |
ºÆ |
ª |
Π|
æŁ |
º |
| æ ª Æ Łæ , Łæ Œ æ , æ |
æº |
Ł |
ı |
ª Æ - |
![]() ,
,
| ª R |
Ł |
ı |
Æ |
Łæ u Œ Æ Łæ e |
e . e |
|
| ˜ Œ |
º æ |
. ˇ æ e e |
æ |
ßØ Æ Łæ, u e |
ßØ Æ |
Łæ, R - |
| Ł |
ı |
u Πe e , e |
æ |
e = R > u . e e |
Ø æ |
ß, Œ |
![]() . ª Ø æ ß, Œ
. ª Ø æ ß, Œ ![]()
| (a ˇ> |e e· R > )u e = (R · a ˇ|e e)> u e . |
||||||
| Œ Œ Œ ß Ł Œ |
a |
Æ |
Łæ u e |
º æ |
Ł æ |
ß , |
a
ˇ>
|u
e
= (R
·a
ˇ|e
e)>
. æ Ł Ł Ł ß, º Ł a
ˇ|u
e = R
·a
ˇ|e
e. ![]()
8.5 ¸Ł Ø ß æ æ
ˇ æ V ºŁ Ø æ æ º k .
˛ º Ł 8.5.1. ˇ æ L Æ Łæ ª æ V ß æ æ Ø Ł ß æ , æºŁ æ Ø Ł æŁ º -
ª æº Ł Ł ł ª Ł , æ
1. (∀ a,b ∈ L ) a + b ∈ L ;
2. (∀ α ∈ k, a ∈ L ) αa ∈ L .
º æ Ł . æ Ø Ł æ L , ææ æ æ Ł Ł ß Ł Ł Ł, Æ ºŁ Ø æ æ .
˜ Œ º æ . L ⊂ V Ł L æ Ø Ł æ , ª L ææ Ł Ł ß ŁŁ ª æº Ł Ł
ł ª Ł . ˇ Œ , (∀ a,b ∈ L ) a − b ∈ L . ˜ Øæ Ł-
º , −b = −(1 · b ) = (−1)b ∈ L , ª a − b = a + (−b ) ∈ L . ŒŁ
Æ , (L, +) Æ Ł Ł ª ª ß (V, +). ˇ ß Ł ŒæŁ ß ºŁ Ø ª æ æ ß º æ L , æ º -
ß ß ŒæŁ ß, æ øŁ æ Œ ł Ł , ß º æ æ æ V
, Æ ß º æ Ł æ Ø Ł æ L
. Ł æ º , L
º æ ºŁ Ø ß æ æ . ![]()
˛ º Ł 8.5.2. ¸Ł Ø ß æ æ æ æ V ß æ æ Œ ª æ Ø Ł æ L , ææ æ
æ Ł Ł ß Ł Ł Ł.
ˇ º Ł 8.5.1. ˇ æ Ł æ Øæ ºŁ Ø ßı -
æ æ ºŁ Ø ª æ æ V æ º æ æ æ æ æ V .
| ˜ Œ |
º æ |
. ´ æ |
º , æ |
{Li } |
æ |
Øæ |
ºŁ |
Ø ßı |
- |
| æ |
æ |
æ æ |
V . — ææ |
Ł |
æ |
![]() .
.
| ˝ |
Œ , L æ |
Ø Ł |
æ |
æ |
æ |
V . |
| ˇ æ |
a,b ∈ L ⇒ (∀ i ) |
a,b ∈ Li . |
ΠΠΠLi |
ºŁ Ø |
- |
æ æ , ![]() . º º , L
. º º , L
| æ |
Ø Ł |
æŁ º |
ª æº Ł . |
|
| º ªŁ |
Œ ß |
æ , |
(∀ α ∈ k,a ∈ L ) |
αa ∈ L . |
º º , L
æ æ æ æ V
. ![]()
| ˇ æ |
A |
æ ºŁ |
Ø ª |
æ æ V . — ææ |
- |
||
| Ł æ ºŁ |
Ø ß |
æ |
æ L |
æ |
æ |
V , æ øŁ |
- |
| æ A . |
ŒŁ |
æ |
æ æ ø æ |
, |
Ł , æ æ |
||
| V . æ Ł |
æ |
Ł æ ı |
Łı |
æ |
æ |
L , æ |
![]() .
.
| ˇ º |
Ł |
8.5.2. æ L (A ) |
Ł |
ł |
ºŁ Ø |
- |
| æ |
æ |
æ æ V , æ ø |
æ |
A . |
||
| ˜ Œ |
º æ |
. ˜ Øæ Ł º , Œ , |
L (A ) |
º æ |
- |
æ æ æ æ V æº Ł º Ł 8.5.1. ˜ º , æ A æ Ł æ æ ı L Œ ß ß æ Œ , æº º
A ⊂ L (A ).
˝ Œ , º Æ ºŁ Ø æ æ L 0 , Œ , A ⊂ L 0 . ª ı Ł æ æ Ł æ Œ ßı æ æ L ,
æº º L
(A
) ⊂ L
0
. ![]()
˛ º Ł 8.5.3. ¸Ł Ø Ø Æ º Œ Ø æ A æ æ V ß æ Ł ł ºŁ Ø æ æ L (A ) æ æ V , æ ø æ A .
æ ª , æ æ L (A ) æ A ŁºŁ æ A .
| ˇ º Ł 8.5.3 (æ |
Ł L (A )). ¸Ł Ø |
Æ º |
Œ L (A ) æ - |
|
| æ Ł Ł æ ºŁ |
Ø ßı Œ ÆŁ ŁØ Œ |
ßı |
æ |
|
| æ A æ Œ Ł Ł |
Ł Ł æ ª |
º |
k , |
æ |
![]() )
)
Ł Ł æ αa = 0 .
˜ Œ º æ . ´ æ º , Æ Ł : ![]() .
.
˝ Æı Ł Œ , L (A ) = L 0 .
Ø æ ß, Œ Œ Œ A ⊂ L (A ) , L (A ) æ Ł º Æ ºŁ-
Ø Œ ÆŁ Ł Œ ª æ æ Œ A ,
æ L 0 ⊂ L (A ).
ª Ø æ ß, æ , L 0 æ Ø Ł æ æ æ V , æº º , L 0 ºŁ Ø æ æ æ æ V .
˚ ª , æ A ⊂ L 0 ( Œ Œ Œ a = 1 · a + 0 · a 1 + 0 · a 2 + ... ).
ª º Ł 8.5.2 L (A ) ⊂ L 0 .
´ Ł ª º , L
(A
) = L
0
. ![]()
º æ Ł 8.5.0.1. ¯æºŁ A = {a 1 ,a 2 ,...,as }, ª Œ ß a 1 ,a 2 ,...,as
º æ ºŁ Ø ŁæŁ ß Ł, L (A ) Œ , dim L (A ) =
= s Ł
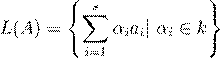 .
.
˜ Œ º æ . ˜ Øæ Ł º , Œ , L (A ) Ł Œ ßØ
Ł æº Ł º Ł 8.5.3. ª Œ ß a
1
,a
2
,...,as
Œ æ Æ Łæ L
(A
), æº º , dim L
(A
) = s
. ![]()
º æ Ł 8.5.0.2. ¯æºŁ ºŁ Ø æ æ V Œ , º Æ ª ºŁ Ø æ æ L Œ º æ Œ ß Ł
dim L 6 dim V . ¯æºŁ dim L = dim V , L = V .
˜ Œ º æ . ´ æ º , æ dim V = n Ł e 1 ,e 2 ,...,en Æ -
Łæ V . Œ Œ Œ L æ æ ºŁ Ø ª æ æ V ,
º Æß Œ ß . ´ Ł æº , Ł Æ æŒ -
æ Ł æ æ L ß Œ º Æß Æ æŒ æ æ æ V .
ˇ æ a 1 ,a 2 ,...,as Æ Łæ L , æ dim L = s . Œ Œ Œ a 1 ,a 2 ,...,as ºŁ Ø ß æ Æ Łæ e 1 ,e 2 ,...,en æ æ V , æØ ºŁ Ø Ø ŁæŁ æ Ł s 6 n , æ dim L 6 dim V .
¯æºŁ dim L = dim V , æ s = n , Œ ß a 1 ,a 2 ,...,an
Œ æ Æ Łæ æ æ V . ´ æŁº º Ł 8.5.3 Æ
Ł
![]()
˛ º Ł 8.5.4. Ø æ Øæ ºŁ Ø ßı æ æ {L i } æ æ V ß æ ºŁ Ø Æ º Œ æ ,
ŁŒ - æ Æœ Ł Ł Æ Łæ ßı æ Łı ºŁØ ßı æ æ , æ
.
![]() ˛ º Ł 8.5.5. Ø æ Øæ ºŁ Ø ßı æ æ {L
i
}
æ æ V
ß æ Ł ł ºŁ Ø æ æ -
˛ º Ł 8.5.5. Ø æ Øæ ºŁ Ø ßı æ æ {L
i
}
æ æ V
ß æ Ł ł ºŁ Ø æ æ -
æ æ V , æ ø æ æ æ ª æ Øæ .
ˇ º Ł 8.5.4 (æ Ł æ ß). L 1 + L 2 ı ºŁ-
Ø ßı æ æ æ æ æ Œ Ł
{a 1 + a 2 | a 1 ∈ L 1 ,a 2 ∈ L 2 }.
˜ Œ º æ . ˜ Øæ Ł º , º Ł 8.5.4 Ł L 1 +L 2 =
= L (L 1 ∪ L 2 ). ´ Æ Ł L 0 = {a 1 + a 2 | ai ∈ Li , i = 1, 2}. ˝ Œ , L 1 + L 2 = L 0 .
Ø æ ß, æ , L 0 æ Ø Ł æ æ æ V , L 0 ºŁ Ø æ æ æ æ V .
˜ º , L 1 ⊂ L 0 . ˜ Øæ Ł º , (∀ a 1 ∈ L 1 ) a 1 = a 1 + 0, ª 0 ∈ L 2 .
º ªŁ , L 2 ⊂ L 0 , Ł (∀ a 2 ∈ L 2 ) a 2 = 0+a 2 , ª 0 ∈ L 1 . ˛ æ ,
L 1 ∪ L 2 ⊂ L 0 , æº º L (L 1 ∪ L 2 ) ⊂ L 0 , æ L 1 + L 2 ⊂ L 0 .
ª Ø æ ß, Ł º ßØ Œ a ∈ L 0 . ¯ª
æ Ł Ł a = a 1 + a 2 , ª a 1 ∈ L 1 , a 2 ∈ L 2 . ´ Œ ß a 1 ,a 2 ∈
| ∈ L 1 ∪ L 2 , æº |
º a = a 1 + a 2 ∈ L (L 1 ∪ L 2 ) = L 1 + L 2 , |
æ |
| a ∈ L 1 + L 2 . ¨ |
L 0 ⊂ L 1 + L 2 . |
ŒŁ Æ , Ł ı Œº ŁØ º , L
1
+ L
2
= L
0
. ![]()
| ˙ |
Ł 8.5.1. Œ , Æø |
æº |
||
| X X Ł Ł L i = a i | a i ∈ L i (i ) (i ) |
æ |
ai = 0 . |
||
| ˛ |
º Ł 8.5.6. ºŁ Ø ßı |
æ |
æ L 1 +L 2 ß - |
|
| æ |
Ø, æºŁ L 1 ∩ L 2 = {0}. |
|||
| ˇ |
æ Æ æ L 1 ⊕ L 2 . |
|||
| ¸ |
8.5.1. ¸ Æ ºŁ Ø ŁæŁ |
æŁæ |
ΠΠ- |
|
| ª ºŁ Ø ª æ æ V |
º Ł Æ Łæ - |
|||
| æ |
æ |
V . |
||
| ˜ Œ |
º æ . ˇ æ a 1 ,a 2 ,...,as ºŁ |
Ø |
ŁæŁ æŁæ |
|
| Π|
Ł V Ł e 1 ,e 2 ,...,en Æ Łæ æ |
æ |
V , dim V = n . — æ- |
|
| æ |
Ł |
æº ø æŁæ Œ |
||
| a 1 ,a 2 ,...,as ,e 1 ,e 2 ,...,en . |
(8.3) |
|||
| ¨ |
Ø æŁæ ß Œ (8.3) º |
Œ ß, Œ ß ºŁ- |
||
| Ø |
ß æ ß øŁ . ˇ ß s |
Œ æ æ |
||
| æ |
, Œ Œ Œ Ł ºŁ Ø ŁæŁ ß . ˇ º Ł |
|||
| a 1 ,a 2 ,...,as ,ei 1 ,ei 2 ,...,ei k . |
(8.4) |
|||
Łæ Œ (8.4) Æ ºŁ Ø ŁæŁ Ø, Œ Œ Œ Ł Ł Œß æ æ º ß Œ ß.
˜ º , º Æ Ø Œ a ∈ V , ºŁ Ø ß æ æŁæ (8.3),
Æ ºŁ Ø ß æ Ł æŁæ (8.4), Œ Œ Œ º ß Œß Ł æŁæ ß (8.3), ºŁ Ø ß æ æŁæ (8.4). ŒŁ
Æ , æŁæ Œ (8.4) Æ æ æ º Æ Łæ æ æ V .
Æ Łæ º Ł æŁæ ß a
1
,a
2
,...,as
Æ º Ł Œ ßı Œ. k
= n
− s
. ![]()
¯˛—¯ 8.5.1 ( æ Ł æ ß ı ºŁ Ø ßı æ æ ). — æ æ ß ı ºŁ Ø ßı æ æ Œ -
ª ºŁ Ø ª æ æ V æ æ Ø Łı
ºŁ Ø ßı æ æ Æ æ Ł Łı æ Ł , æ
dim (L 1 + L 2 ) = dim L 1 + dim L 2 − dim (L 1 ∩ L 2 ).
| ˜ Œ º æ . ˇ æ L 1 Ł L 2 ºŁ Ø ßı |
æ |
æ |
- |
||
| æ |
æ V . ˛Æ Ł L = L 1 ∩ L 2 . ˇ æ |
æŁæ |
Π|
||
| e 1 ,e 2 ,...,er |
(8.5) |
||||
| Æ Łæ L . ¯æºŁ L = {0}, r = 0 Ł Æ Łæ Æ |
æ |
æ . |
|||
| ˇ |
º Æ Łæ L º Ł Æ Łæ L 1 |
||||
| e 1 ,e 2 ,...,er ,ur +1 ,...,us , |
(8.6) |
||||
| ª |
(8.6) Æ Łæ L 1 , dim L 1 = s . º ªŁ , º Ł Æ Łæ L 2 |
º |
Æ |
Łæ L |
|
| e 1 ,e 2 ,...,er ,vr +1 ,...,vt , |
(8.7) |
||||
| ª |
(8.7) Æ Łæ L 2 , dim L 2 = t . — ææ Ł æº ø æŁæ Œ |
||||
e 1 ,e 2 ,...,er ,ur +1 ,...,us ,vr +1 ,...,vt . (8.8)
ˇ Œ æŁæ (8.8) º æ Æ Łæ L 1 + L 2 . ˜ Øæ Ł º ,
Ł º ßØ Œ x ∈ L 1 + L 2 . ª x = a + b , ª a ∈ L 1 , b ∈ L 2 . — º ª Œ a Æ Łæ (8.6), Œ b Æ Łæ (8.7) Ł
挺 ß º ß ß Ł , ß º Ł , Œ x ºŁ Ø ß æ æŁæ (8.8).
˛æ æ Œ , æŁæ Œ (8.8) º æ ºŁ Ø -
ŁæŁ Ø. — ææ Ł ºŁ Ø Œ ÆŁ Ł
α 1e 1 +... +α r e r +β r +1u r +1 +... +β s u s +γ r +1v r +1 +... +γ t v t = 0. (8.9)
˝ Œ , æ æŒ º ß α i ,β i ,γ i = 0. — ææ Ł Œ
x = α 1 e 1 + ... + αr er + βr +1 ur +1 + ... + βs us . (8.10)
¨ æ (8.9) Ł , Œ
x = −γr +1 vr +1 − ... − γt vt . (8.11)
— æ (8.10) Œ ß , Œ x ∈ L 1 , æ (8.11)
Œ ß , Œ x ∈ L 2 , æº º x ∈ L 1 ∩ L 2 = L .
º º , Œ x ß Ł Æ Łæ L .
![]() .
(8.12)
.
(8.12)
Ł (8.10) Ł (8.12). ´ß Ł Œ x Æ Łæ (8.6) º
Æß Ł æ ß , ª
![]() .
.
ª æ (8.9) Ł Ł Ł
α 1 e 1 + ... + αr er + γr +1 vr +1 + ... + γt vt = 0. (8.13)
Œ Œ Œ Æ Łæ (8.7) º æ ºŁ Ø ŁæŁ Ø æŁæ Ø Œ ,
Ł æ (8.13) æº , æ æŒ º ß α 1 = ... = αr = γr +1 =
= ... = γt = 0.
´Ł , æŁæ Œ (8.8) º æ ºŁ Ø ŁæŁ Ø, æº º , æŁæ Œ (8.8) º æ Æ Łæ L 1 + L 2 . ª
dim (L 1 +L 2 ) = Łæº Œ Æ Łæ (8.8) = r +(s −r )+(t −r ) = s +
+t
−r
= dim L
1
+dim L
2
−dim L
= dim L
1
++dim L
2
−dim
(L
1
∩L
2
). ![]()
º æ Ł 8.5.1.1. — æ Ø æ ß æ æ Ø æº ª ßı.
˜ Œ º æ . ˜ Øæ Ł º , æºŁ L 1 + L 2 æ ,
º Ł L 1 ∩L 2 = {0}, dim {0} = 0. ˇ º , dim (L 1 ⊕L 2 ) =
= dim L
1
+ dim L
2
. ![]()
ˆº 9
¸Ł Ø ß ß ºŁ Ø æ æ
9.1 ˇ æ æ Ł ºª Æ ºŁ Ø ßı
ˇ æ V Ł V 0 ºŁ Ø ßı æ æ Ł Ł æ ß º k .
˛ º Ł 9.1.1. ¸Ł Ø ß Ł æ æ V æ æ V 0 Ł Ł º k ß æ æ Œ Æ Ł f : V → V 0 , º ø æº Ł :
1. (∀ a,b ∈ V ) f (a + b ) = f (a ) + f (b );
2. (∀ α ∈ k,a ∈ V ) f (αa ) = αf (a ).
´Ł , Ł ºŁ Ø ßØ ¿ º æ Æ Æø Ł -
Ł Ł Ł ¿. ´ æº Ł Ł , Æ º æ Æß f Æߺ
ÆŁ Œ Ł Ø. æº Ł 1) , f º æ ª Ł (V, +)
![]() . æº Ł 1) ß æ æº Ł Ł Ł æ Ł, æº Ł 2) ß æ æº Ł æ Ł.
. æº Ł 1) ß æ æº Ł Ł Ł æ Ł, æº Ł 2) ß æ æº Ł æ Ł.
˛ º Ł 9.1.2. ¸Ł Ø ß Ł æ æ V æ æ V 0 Ł Ł æ ß º k ß æ æ Œ
58
9.1. ˇ æ æ Ł ºª Æ ºŁ Ø ßı
Æ Ł f : V → V 0 , º ø æº Ł ºŁ Ø æ Ł:
(∀ α,β ∈ k, a,b ∈ V ) f (αa + βb ) = αf (a ) + βf (b ).
˛Æ Ł L (V,V 0 ) æ æ ı ºŁ Ø ßı Ł æ æ V æ æ V 0 . ˝ æ ææ Ł
ºª Æ Ł æŒŁ ŁŁ: æº Ł Ł ł Ł .
˛ º Ł 9.1.3. ˇ æ f,g ∈ L (V,V 0 ) Ł α ∈ k . ˇ º ª , (f +
g )(a ) = f (a ) + g (a ) Ł (αf )(a ) = αf (a ).
˛ º Ł 9.1.3 Œ Œ æ ßæº , f + g Ł αf º æ ºŁ Ø ß Ł Ł.
˜ Øæ Ł º , (∀ α,β ∈ k, a,b ∈ V ) (f +g )(αa +βb ) = f (αa +βb )+
+g (αa +βb ) = αf (a )+βf (b )+αg (a )+βg (b ) = α (f (a )+g (a ))+β (f (b )+
+ g (b )) = α (f + g )(a ) + β (f + g )(b ). º º f + g ∈ L (V,V 0 ).
¯ø ø Œ ß æ , αf ∈ L (V,V 0 ).
¯˛—¯ 9.1.1. æ L (V,V 0 ), ææ æ æ -
º ß Ł Ø ºª Æ Ł æŒ Ø Ł Ø æº Ł Ł ł Ø ºª Æ Ł æŒ Ø Ł Ø Ł , Æ ºŁ Ø æ æ º k .
˜ Œ º æ . ˇ æ f,g,h ∈ L (V,V 0 ),α,β, 1 ∈ k . ˜º Œ º æ ß æ Œ , ß º æ 7 ŒæŁ ºŁ Ø ª æ æ , Ł
1. f + g = g + f ;
2. f + (g + h ) = (f + g ) + h ;
3. (∀ f,g )(∃ h ) g + h = f ;
4. α (f + g ) = αf + αg ;
5. (α + β )f = αf + βf ;
6. (αβ )f = α (βf ) = β (αf );
7. 1 · f = f .
ˇ Ł Œ ß Ł Łı.
1) ¨ (∀ a ∈ V ) (f +g )(a ) = f (a )+g (a ) = g (a )+f (a ) = (g +f )(a ).
º º , f + g = g + f .
3) ¨ f,g ∈ L (V,V 0 ). — ææ Ł Æ Ł h : V → V 0 , -
º æº øŁ Æ (∀ a ∈ V ) h (a ) = f (a ) − g (a ). ¸ ªŒ -
| Π|
, |
Æ |
Ł |
º æº |
Ł ºŁ Ø æ Ł, æº - |
| º |
, h ∈ L (V,V 0 ). ˇ |
æ Ł |
(∀ a ∈ V ) |
(g +h )(a ) = g (a )+h (a ) = |
= g
(a
) + (f
(a
) − g
(a
)) = f
(a
). º º , g
+ h
= f
. ![]()
| ˇ æ V,V 0 ,V 00 Ł ºŁ Ø ßı |
æ æ |
º k , |
æ |
|
| f ∈ L (V,V 0 ), ϕ ∈ L (V 0 ,V 00 ). ª |
ææ |
Ł |
Π|
Ł Ł |
| ºŁ Ø ßı ϕ ◦f : V → V 00 , Œ |
º |
æ æº |
øŁ |
|
| Æ (ϕ ◦ f )(a ) = ϕ (f (a )). Œ |
Ł Ł |
ϕ ◦ f Æ |
Æ |
ϕf .
ˇ Œ , ϕf æ ºŁ Ø ßØ Ł æ æ V V 00 .
˜ Øæ Ł º , ϕf (αa + βb ) = ϕ (f (αa + βb )) = ϕ (αf (a ) + βf (b )) = = αϕ (f (a )) + βϕ (f (b )) = α (ϕf )(a ) + β (ϕf )(b ). º º , ϕf ∈
∈ L (V,V 00 ).
¯˛—¯ 9.1.2. ˇ æ f,g ∈ L (V,V 0 ), ϕ,ψ ∈ L (V 0 ,V 00 ), h ∈ L (V 00 ,V 000 ), α ∈ k . ª æ ºŁ ß æº øŁ æ ł Ł :
1. ϕ (f + g ) = ϕf + ϕg ;
2. (ϕ + ψ )f = ϕf + ψf ;
3. h (ϕf ) = (hϕ )f ;
4. α (ϕf ) = (αϕ )f = ϕ (αf ).
9.1. ˇ æ æ Ł ºª Æ ºŁ Ø ßı
| ˇ æ f,g,ϕ,ψ,h ∈ L (V,V ), æ ºŁ Ø ß Ø ª æ æ V æ Æ . |
ß Ł ºŁ- |
||
| ˛ º Ł 9.1.4. ¸Ł Ø ßØ Ł V V ß æ Ł . |
- |
||
| ˝ æ L (V,V ) ææ Ł ºª Æ |
Ł æŒ |
||
| Ł Ł . ¯æºŁ f,ϕ ∈ L (V,V ), |
º ª |
||
| ϕf = ϕ ◦ f : V → V , ϕf ∈ L (V,V ). ˜º |
Ø |
ŁŁ |
Ł |
| æ ºŁ ß æ ł Ł 1) 4) |
ß 9.1.2. |
||
| ¯˛—¯ 9.1.3. æ L (V,V ), ææ |
æ |
æ - |
|
| º ß Ł ºª Æ Ł æŒŁ Ł |
Ł Ł: |
Ł Ł |
|
| æº Ł Ł Ł Ł ł Ł º k . |
Ł |
, Æ |
ºª Æ |
| 9.1.3 , ŁŁ æº øŁ 10 ŒæŁ : 1) 7) ŒæŁ ß ºŁ Ø ª æ æ ; 8) f (g + h ) = fg + fh , (f + g )h = fh + gh ; 9) f (gh ) = (fg )h ; 10) α (fg ) = (αf )g = f (αg ). |
æ |
L (V,V ) |
º - |
| ˚ Œ Ł æ Œ ºª Æ , ºª Æ ºŁ Ø ßı |
æ æ |
Ł Ł |
|
ı ºª Æ Ł æŒŁı æ Œ : æ Œ ß ºŁ Ø ª æ æ ( ŒæŁ ß 1) 7)) Ł æ Œ ß Œ º ( ŒæŁ ß 1) 3) Ł 8) 9)). Ł æ Œ ß æ ß æ Æ Ø æ Øæ 10).
´ º ł Øł , æ L (V,V ) Æ Æ L (V ). ˇ Ł ß :
1) ˝ º Ø ºŁ Ø ßØ Ł L (V ) . ˛ Æ æ 0V .
˛ º æ ŒŁ Æ (∀ a ∈ V ) 0V (a ) = 0. æ ,
(∀ f ∈ L (V )) f + 0V = f .
| 2) æ ßØ ºŁ Ø ßØ Ł L (V ) . ˛Æ |
æ 1V . |
|||
| ˛ º æ ŒŁ Æ (∀ a ∈ V ) 1V (a ) |
= |
a . æ , |
||
| (∀ f ∈ L (V )) 1V · f = f · 1V = f . |
, |
ºª Æ L (V ) |
||
| æ Ł Ł . |
||||
| 9.2 Ł ºŁ |
Ø ª |
Π|
||
| ºŁ Ø |
æ æ |
|||
| ˙ æ ß º Ł Æ ª dim V = n . |
Ł æ ı ºŁ Ø ßı |
ºª Æ ß L (V ) , |
||
| ¯˛—¯ 9.2.1. ˇ æ |
e 1 ,e 2 ,...,en Æ |
Łæ ºŁ |
Ø |
ª æ - |
| æ V . ˇ æ V 0 |
ª ºŁ Ø æ |
æ |
º k Ł |
|
![]() Ł º æŁæ Œ Ł V
0
. ª æ ø æ -
Ł º æŁæ Œ Ł V
0
. ª æ ø æ -
| Ł æ |
ßØ ºŁ |
Ø ßØ |
f ∈ L (V,V 0 ), |
øŁØ Æ Łæ |
|
| æ æ |
V |
æŁæ |
Œ æ |
æ |
V 0, |
æ
![]() .
.
˜ Œ º æ . 1) ¯ Ł æ æ .
ˇ æ æ ø æ ºŁ Ø ßØ f ∈ L (V,V 0 ) Œ Ø, (∀ 1 6
6 i
6 n
) f
(ei
) = a
0
i
. ¸ Æ Ø Œ a
∈ V
æ Ł Ł ![]() . ª
. ª
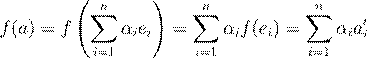 .
.
˜ æ Ł , æ ø æ ª Ø ºŁ Ø ßØ f 1 ∈ L (V,V 0 ) , -
º øŁØ æº Ł ![]() . ª
. ª
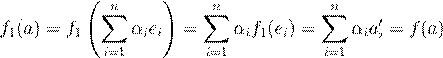 .
.
º º f 1 = f .
2) ø æ Ł .
ˇ æ a
∈ V
. ª ![]() n
. ˛ ºŁ Æ Ł f
: V
→ V
0
æº øŁ Æ
n
. ˛ ºŁ Æ Ł f
: V
→ V
0
æº øŁ Æ
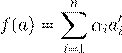 .
.
ˇ Œ , Æ Ł º æº Ł ºŁ Ø æ Ł. ˜ Øæ Ł º , æ ![]() . ª
. ª
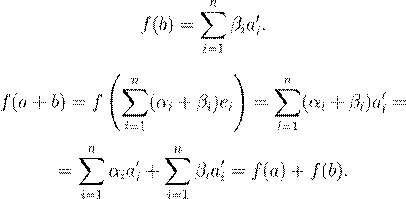
¯ø ø Œ ß æ , f (αa ) = αf (a ), ª α ∈ k . ŒŁ Æ ,
Æ Ł f ∈ L (V,V 0 ). ˝ Œ , (∀ 1 6 i 6 1) f (ei ) = f (0·e 1 +... +
![]() .
. ![]()
º æ Ł 9.2.1.1. ¸Ł Ø ßØ Ł V V 0 º æ Æ Ł Æ Łæ ßı Œ æ æ V . ß Œ Ł Œ º æ Ø æ Ł ß 9.2.1.
| º æ Ł 9.2.1.2. |
æ |
ºŁ |
Ø ßı |
Ł V V 0 |
ı Ł - |
|
| æ Ł |
æ |
æ ŁŁ æ |
æ |
ßı |
||
| æŁæ Ł n - |
Π|
æ |
æ |
V . |
||
| ˇ æ V |
ºŁ Ø |
æ |
æ |
º k , dim V |
= n , |
|
| e 1 ,e 2 ,...,en |
Æ Łæ |
æ |
æ |
V . ˇ æ , |
º , f ∈ L (V ), |
æº - |
| æ Ł Ł |
ß 9.2.1, |
Ł æ |
ß Æ |
º - |
||
| æ Æ |
Ł Æ Łæ ßı |
Π|
f (e 1 ),f (e 2 ),...,f (en ) ∈ V . — |
º Ł |
||
Ł Æ ß Æ Łæ æ æ V , º Ł
f (e 1) = α 11e 1 + α 12e 2 + ... + α 1n e n ;
f (e 2 ) = α 21 e 1 + α 22 e 2 + ... + α 2n en ; (9.1)
...
f (e n ) = α n 1e 1 + α n 2e 2 + ... + α nn e n .
| ˛ º Ł 9.2.1. Ł Ø ºŁ |
Ø |
ª |
f ∈ L (V ) - |
|
| æŁ º Æ Łæ e 1 ,e 2 ,...,en ß |
æ |
Ł |
, |
æ Ł Œ |
| Ł , æ æ º Ø Ł Œ Ł Ł Æ Łæ ßı Œ Æ Łæ. |
ºŁ Ø |
ª |
ß Ł Æ |
|
| > α 11 α 12 ... α 1n α 21 α 22 ... α 2n A f |e e = ... ... ... ... α n 1 α n 2 ... α nn |
= |
α 11 α 12 ... α 1n |
α 21 α 22 ... α 2n |
... αn 1 ... αn 2 . ... ... ... αnn |
| ˛ º Ł 9.2.2. Ł Ø ºŁ Ø |
ª |
f ∈ L (V ) æŁ- |
||
| º Æ Łæ e 1 ,e 2 ,...,en ß æ |
Ł , æ |
ºÆ |
Ł Œ Ø º - |
|
| æ Œ Ł ß æ ºÆ ß Œ f (e 1 ),f (e 2 ),...,f (en ) æŁ º - |
||||
![]() Łæ e
, æ
Łæ e
, æ
e
Af | e e = (f ˇ (e 1 )|e e,f ˇ (e 2 )|e e,...,f ˇ (en )|e e).
˛ º Ł 9.2.3. ¯æºŁ Æ Ł
e 1 f (e 1 )
e 2 f (e 2 )
e = Ł f (e ) = , e ... e ...
en f (en )
![]() Ø ºŁ Ø ª f
æŁ º Æ Łæ e
ß æ
Ø ºŁ Ø ª f
æŁ º Æ Łæ e
ß æ
e
Ł Af , º Ł æ
f (e e) = A > f e. e
¯˛—¯ 9.2.2. ˇ Ł ŁŒæŁ Æ Łæ e e ºŁ Ø ª æ æ V , dim V = n , Æ Ł σ : L (V ) → M (n,k ), æ æ º ø
ºŁ Ø f
ª Ł æŁ º Æ Łæ ![]() ),
),
º æ Ł Ł ºª Æ ß ºŁ Ø ßı L (V ) ºª Æ Œ ßı Ł n -ª Œ M (n,k ).
˜ Œ º æ . ˇ e e Œ ßØ Æ Łæ æ æ V . — ææ Ł
Æ Ł σ : L (V ) → M (n,k ), σ (f ) = Af , ª Af Ł ºŁ Ø-
ª f æŁ º Æ Łæ e e . ˇ Œ , Æ Ł º æ Ł Ł .
1) ¨ œ Œ Ł æ σ .
ˇ æ σ (f ) = σ (g ), ª f,g ∈ L (V ). , Af = Ag ⇒
![]() . ß º ŁºŁ, Æ ß
. ß º ŁºŁ, Æ ß
Æ Łæ ßı º æ æ V æ . ª æº æ Ł Ł ß 9.2.1 æº , f = g .
2) œ Œ Ł æ σ .
ˇ æ A ∈ M (n,k ). ˇ æ Ł n Œ æ æ V Œ, Æß Œ Ł ß æ ºÆ ß Łı Œ æŁ º Æ Łæ e e æ ºŁ æ æ ºÆ Ł Ł ß A . ª 9.2.1 æ ø æ ºŁ Ø ßØ f ∈ L (V ), øŁØ Æ Łæ e e æ ß Ł Œ ß.
ˇ æ Ł Æ Ł ![]() . ˛ æ Ł , æºŁ æ Ł
. ˛ æ Ł , æºŁ æ Ł
æ º Ł 9.2.3, A > = A > f . ŒŁ Æ , σ (f ) = Af = A .
3) ı Ł ŁØ.
ˇ æ f,g
∈ L
(V
) Ł Af
,Ag
Ł ß Łı ºŁ Ø ßı æŁ º Æ Łæ e
e
. ª ![]() .
.
— ææ Ł Øæ Ł æ ß ºŁ Ø ßı f + g Æ Łæ ß
Œ ß. Ø æ ß, ![]() .
.
ª Ø æ ß, ![]()
= (Af + Ag )> e .
˛ æ , 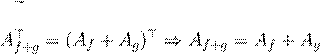 . ŒŁ Æ , -
. ŒŁ Æ , -
Ł æ ß ºŁ Ø ßı æ Ł Łı . º º
σ (f + g ) = Af +g = Af + Ag = σ (f ) + σ (g ), æ Æ Ł σ æ ı æº Ł .
— ææ Ł Øæ Ł Ł Ł ºŁ Ø ßı fg
Æ Łæ ß Œ ß. Ø æ ß, ![]() .
.
ª Ø æ ß, ![]()
![]() .
.
˛ æ , A >fg = (A f A g )> ⇒ A fg = A f A g , æ Ł Ł -
Ł ºŁ Ø ßı Ł Ł Ł Łı . º º
σ (fg ) = Afg = Af Ag = σ (f )σ (g ),
| æ |
Æ |
Ł σ æ ı |
Ł . |
|||
| ˝ Œ |
, æ |
æ æ |
Π|
ß |
æ , |
Aαf = αAf ⇒ σ (αf ) = |
= ασ
(f
), ª α
∈ k
. ![]()
| ˇ º Ł |
9.2.1. ˚ |
Ł ßØ æ ºÆ Æ |
Π|
Ł Ø- |
| æ ŁŁ ºŁ Ø ß |
Œ Ł æ |
ºÆ |
ª Œ- |
|
| , æ |
æº |
Ł ª ºŁ Ø f (ˇ a ) = Af a. ˇ |
ª |
, |
| ˜ Œ º æ |
. ˜ Øæ Ł |
º , Œ a = a ˇ> e e . |
Ø æ ß, |
![]() . ª Ø æ ß,
. ª Ø æ ß,![]()
![]() . ¨ , f
(ˇ
a
)>
= (Af
a
ˇ)>
⇒ f
(ˇ
a
) = Af
a
ˇ.
. ¨ , f
(ˇ
a
)>
= (Af
a
ˇ)>
⇒ f
(ˇ
a
) = Af
a
ˇ. ![]()
˛ º Ł 9.2.4. Ł B ß æ Æ Ø Ł A (B ∼
A ) º k , æºŁ æ ø æ æ Æ Ł Q æ º Ł Ł º k Œ ,
B = Q −1 AQ.
| ¨ ª ª , Ł B º |
æ Ł |
Ł - |
| Ł ß A æ ø Ł ß Q , ŁºŁ Ł Ł ß A æ ø Ł ß Q . |
B Æ |
Ł - |
| ˙ Ł 9.2.1. ¯æºŁ Ł ß B Ł A Œ ß Ł Ł Œ Ø æ Ł. |
Æ ß, Ł |
º ß Æß |
| ˇ º Ł 9.2.2. ˛ ł Ł ÆŁ Ł º æ Ł æ M (n,k ). ˜ Œ º æ . 1) — º ŒæŁ æ . |
º æ |
ł Ł Œ- |
| ¨ A = E −1 AE , ª A ∼ A , º Ł . 2) Ł Ł æ . |
Ł ß Q Łª |
Ł Ł |
| ˇ æ B ∼ A . , (∃ Q, |Q | 6= 0) B = Q −1 AQ ⇒ ⇒ QBQ −1 = Q (Q −1AQ )Q −1 ⇒ QBQ −1 = A ⇒ A = (Q −1)−1BQ −1 ⇒ ⇒ A ∼ B , º Ł ß Q Łª Q −1 . 3) Ł Ł æ . |
||
ˇ æ C ∼ B, B ∼ A , ª (∃ R, |R | 6= 0) C = R −1 BR , Ł
(∃ Q,
|Q
| 6= 0) B
= Q
−1
AQ
. º º C
= R
−1
(Q
−1
AQ
)R
= = (QR
)−1
A
(QR
) ⇒ C
∼ A
, º Ł ß Q
Łª QR
. ![]()
| ¯˛—¯ 9.2.3. |
Ł ß ª Ł ª ºŁ |
Ø ª |
f |
||
| ºŁ ßı Æ |
Łæ ı |
Æ ß. ˇ Ł Ł |
A f |u º e |
æ |
Ł |
| Ł ß A f |e e |
æ |
Ł Ł Ł øŁ |
Ł ß |
ı |
|
| Æ Łæ e Œ Æ Łæ e |
u , e |
æ A f |u = Q −1A f |e Q, e e |
|||
| ª Q Ł |
ı e Œ u . |
||||
e e
˜ Œ º æ . ˇ æ dim V = n, e e Ł u e Æ Łæ æ æ
V , f ∈ L (V ), Af | e e Ł Af | u e Ł ß f æŁ º e e Ł u e æ æ . ª
![]()
ˇ æ , Œ , Q
Ł ı ![]() Œ , æ
Œ , æ ![]() .
.
Ø æ ß, ![]()
= (Af
|
e
Q
)>
e
e. ª Ø æ ß, ![]()
![]() . ŒŁ Æ ,
. ŒŁ Æ , ![]()
![]() .
. ![]()
| º æ |
Ł 9.2.3.1. ¯æºŁ Af |
Ł ºŁ Ø ª |
f æŁ- |
| º |
Æ Łæ e e Ł B ∼ Af , |
Ł B ææ |
Ł Œ Œ |
| Ł æ . |
ºŁ Ø ª f |
æŁ º Œ ª |
ª ª Æ Ł- |
| ˜ Œ |
º æ . ˜ Øæ Ł º , |
Œ Œ Œ B ∼ Af , |
(∃ Q, |Q | 6= |
| 6= 0) |
B = Q −1 Af Q . — ææ Ł |
ßØ Æ Łæ u e = Q > e e . |
ΠΠΠQ |
| æ Æ |
Ł , u e Æ ß Æ Łæ . ˇ |
9.2.3 Ł |
|
![]() .
. ![]()
| 9.3 — ª Ł |
Œ ºŁ Ø ª |
|||||
| ˇ æ V Ł V 0 ∈ L (V,V 0 ). |
ºŁ Ø ßı æ |
æ |
º |
k , |
æ |
f ∈ |
˛ º Ł 9.3.1. ˛Æ ºŁ Ø ª f (Im f ) ß æ æ Æ æ ı º æ æ V . ºŁ Ø ª f (Ker f ) ß æ æ ı Œ æ æ V , Œ ß Ł Æ ŁŁ f æ º æ æ V 0 .
¨ ª º Ł Ł ,
Im f = {f (a )| a ∈ V }, Ker f = {a ∈ V | f (a ) = 0}.
9.3. — ª Ł Œ ºŁ Ø ª
ˇ º Ł 9.3.1. Ł Æ ºŁ Ø ª f ∈ L (V,V 0 )
º æ ºŁ Ø ß Ł æ æ Ł æ æ V Ł V 0 æ æ .
˜ Œ º æ . ˜ Øæ Ł º , (∀ α,β ∈ k,a,b ∈ Ker f ) Ł
f (αa + βb ) = αf (a ) + βf (b ) = α · 0 + β · 0 = 0 ⇒ αa + βb ∈ Ker f.
, Ker f º æ æ Ø Ł ß æ æ æ V , æº º , º æ ª ºŁ Ø ß æ æ .
ˇ æ a 0 ,b 0 ∈ Imf . , (∃ a,b ∈ V ) f (a ) = a 0 ,f (b ) = b 0 .
ª (∀ α,β ∈ k,a 0 ,b 0 ∈ Im f ) Ł
αa 0 + βb 0 = αf (a ) + βf (b ) = f (αa + βb ) ∈ Im f.
˛ æ Im f
º æ æ Ø Ł ß æ æ æ V
0
, æº º , º æ ª ºŁ Ø ß æ æ . ![]()
| ˇ º Ł 9.3.2. ¯æºŁ V |
Π|
ºŁ |
Ø |
æ |
æ |
||
| Ł f ∈ L (V,V 0 ), Ł Æ |
ºŁ |
Ø |
ª |
f |
º |
æ |
Π- |
ß Ł ºŁ Ø ß Ł æ æ Ł.
˜ Œ º æ . ´ æ º , Œ Œ Œ V Œ ºŁ Ø æ æ , Ł º Æ ª æ æ , æ æ Ł Ker f , Œ º æ Œ ß .
ˇ Ø Œ Æ Im f . ˇ æ e 1 ,e 2 ,...,en Æ Łæ æ æ V .
ª![]() . ª
. ª
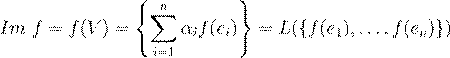 .
.
˝ ºŁ Ø Æ º Œ , Œ ß Łæº Œ , º æ Œ Ø Ł Ł
dim L ({f (e 1 ),...,f (en )}) = rang {f (e 1 ),...,f (en )}.
º º , Im f º æ Œ ß ºŁ Ø ß æ -
æ . ![]()
˛ º Ł 9.3.2. ¯æºŁ V Œ ºŁ Ø æ æ
Ł f ∈ L (V,V 0 ), ª ºŁ Ø ª f r (f ) ß æ æ ª Æ , Œ ºŁ Ø ª f d (f ) ß æ æ ª .
¨ ª º Ł Ł , r (f ) = dim Im f , d (f ) =
= dim Ker f .
º æ Ł . r (f ) = r {f (e 1 ),...,f (en )}.
º æ Ł . ¯æºŁ f ∈ L (V ) , ª ºŁ Ø ª f ª Ł ß ª ºŁ Ø ª æŁ º º Æ ª Æ Łæ , æ
r (f ) = r (Af ).
˜ Œ º æ . ˜ Øæ Ł º , ß ø æº æ Ł Ł
r (f ) = r {f (e 1 ),...,f (en )}. — ææ Ł æ ßØ Ł Ł σ :
V
→ k
n
æŁ º Æ Łæ![]() . ª
. ª ![]() . ˇ Ł Ł Ł ª æŁæ ß Œ Ł æ ,
. ˇ Ł Ł Ł ª æŁæ ß Œ Ł æ ,
![]() .
.
![]()
| ¯˛—¯ |
9.3.1 ( ª Ł Œ ºŁ Ø ª ). ¯æºŁ |
| V Π|
ºŁ Ø æ æ , dim V = n , f ∈ L (V,V 0 ), |
| æ |
ª Ł Œ ºŁ Ø ª f æ Ł |
| æ æ |
V , æ r (f ) + d (f ) = n . |
| ˜ Œ º æ |
. ´ Æ Ł d = d (f ) = dim Ker f . ˇ æ |
| e 1 ,e 2 ,...,ed |
Æ Łæ Ker f . ˜ º Ł Æ Łæ Æ Łæ æ - |
| æ V , º |
Ł e 1 ,e 2 ,...,ed ,ed +1 ,...,en Æ Łæ V . ˇ æº æ Ł Œ |
| º Ł |
9.3.2 Ł |
r (f ) = r {f (e 1 ),f (e 2 ),...,f (ed ),f (ed +1 ),...,f (en )} = r {f (ed +1 ),...,f (en )}.
9.4. ˛Æ Ł æ ºŁ Ø ª
ˇ Œ , Œ ß f (ed +1 ),...,f (en ) º æ ºŁ Ø ŁæŁ ß-
Ł. ˇ æ
αd +1 f (ed +1 ) + ... + αn f (en ) = 0;
f (α d +1e d +1 + ... + α n e n ) = 0 ⇒ α d +1e d +1 + ... + α n e n ∈ Ker f.
— º Ł º Æ Łæ Ker f . ¨
α d +1e d +1 + ... + α n e n = β 1e 1 + ... + β d e d ;
−β 1e 1 − ... − β d e d + α d +1e d +1 + ... + α n e n = 0.
Œ Œ Œ e 1 ,e 2 ,...,en Æ Łæ æ æ V , β 1 = ... = βd = αd +1 =
= ...
= αn
= 0. ŒŁ Æ , Œ ß f
(ed
+1
),...,f
(en
) º æ ºŁ Ø ŁæŁ ß Ł. ª r
(f
) = r
{f
(ed
+1
),...,f
(en
)} = n
− d
⇒ ⇒ r
(f
) + d
(f
) = n
− d
+ d
= n
. ![]()
9.4 ˛Æ Ł æ ºŁ Ø ª
| ˇ æ V ºŁ Ø æ æ º k . — ææ Ł ºª Æ |
|
| L (V ) . ´ Ø ºª Æ æ Ł Ł , º Ł Ł ß ß º æ ßØ 1V . ˝ Ł , (∀ a ∈ V ) 1V (a ) = a . |
- |
| ˛ º Ł 9.4.1. ¸Ł Ø ßØ f ∈ L (V ) ß æ |
Æ - |
| Ł ß , æºŁ Æ Ł Œ Œ º º Ł ºŁŒ Ł Ø º ª Œ º L (V ), æ (∃ f −1 ∈ L (V )) ff −1 = f −1 f = 1V . |
ß |
| ¯˛—¯ 9.4.1 (Œ Ł ŁØ Æ Ł æ Ł ºŁ Ø ª |
). |
| ˜º ª , Æß ºŁ Ø ßØ f ∈ L (V ) Æߺ Æ Ł ß |
Æ- |
| ı Ł Ł æ , Æß Œ Œ Æ Ł Æߺ ÆŁ Œ Ł |
ß . |
| ˜ ªŁ Ł æº Ł, f Æ Ł ª Ł º Œ ª , Œ ª f Ł Ł V V . ˜ Œ º æ . 1) ˝ Æı Ł æ . |
Ł - |
ˇ æ f ∈ L (V ) º æ Æ Ł ß . ˇ º Ł 9.4.1 (∃ f −1 ∈
L (V )) ff −1 = f −1 f = 1V . ˝ Œ , f º æ ÆŁ Œ Ł Ø.
ˇ æ f (a ) = f (b ). ˇ Ł Ł Œ æ Æ Ł f −1, º -
Ł f −1 (f (a )) = f −1 (f (b )) ⇒ (f −1 f )(a ) = (f −1 f )(b ) ⇒ 1V (a ) = 1V (b ) ⇒
⇒ a = b . ˇ æ b ∈ V . ˝ Œ , (∃ a ∈ V ) f (a ) = b . ˇ æ -
Ł Œ b Œ a = f −1 (b ). ª f (a ) = f (f −1 (b )) =
= (ff −1 )(b ) = 1V (b ) = b , æ f º æ ÆŁ Œ Ł Ø.
2) ˜ æ æ .
ˇ æ ∈ L (V ) Ł f º æ ÆŁ Œ Ł Ø. ª (∃ f −1 : V → V ) ff −1 =
= ff −1 = 1V . Æ Ł f −1 Œ º æ ÆŁ Œ Ł Ø. ˝
Œ , f −1 ∈ L (V ), æ f −1 º æº Ł ºŁ Ø-
æ Ł. ˇ æ a,b ∈ V , ª (∃ a 0 ,b 0 ∈ V ) f (a 0 ) = a,f (b 0 ) = b . ˛ æ f −1 (a ) = a 0 , f −1 (b ) = b 0 . ´ Ł º ß α,β ∈ k , æ æ Ł
f (αa 0 + βb 0 ) = αf (a 0 ) + βf (b 0 ) = αa + βb ⇒
⇒ f −1 (αa + βb ) = αa 0 + βb 0 = αf −1 (a ) + βf −1 (b ).
˛ Æ Ł f −1 º æº Ł ºŁ Ø æ Ł, æº º
f
−1
∈ L
(V
). ![]()
| 9.5 Œ Łæ Ł æŒŁØ |
ª º |
Ł ß Ł ºŁ- |
||||
| Ø |
ª |
|||||
| ˇ æ k æ |
º Ł k [λ ] Œ º |
ª |
º |
Ł |
æ ª λ . |
|
| ˛ º Ł |
9.5.1. λ - Ł Ø ( |
ª º |
Ø |
Ł |
Ø) |
º |
| k ß æ |
Ł , º Ł Œ |
Ø |
º æ |
º |
ß Œ º |
|
| k [λ ], æ |
ª º ß λ æ Œ |
Ł Ł |
Ł Ł |
º |
k . |
|
| λ - Ł ß |
挺 ß , |
, |
æŒ º ß |
|||
| Łº , Ł æŒ º |
ß |
Ł ß. ˇ æ |
A = |
|||
![]() = (αij
), αij
∈ k, i,j
= 1,n
. ŒŁ Ł ß Æ ß æŒ º ß Ł.
= (αij
), αij
∈ k, i,j
= 1,n
. ŒŁ Ł ß Æ ß æŒ º ß Ł.
9.5. Œ Łæ Ł æŒŁØ ª º Ł ß Ł ºŁ Ø ª
˛ º Ł 9.5.2. Œ Łæ Ł æŒ Ø Ł Ø º Œ Ø æŒ º Ø Ł ß A ß æ λ - Ł Ł λE − A , æ
| λ − α 11 −α 12 ... −α 1n α 21 λ − α 22 ... α 2n λE − A = . ... ... ... ... −α n 1 −α n 2 ... λ − α nn |
||
| ˛ º Ł 9.5.3. Œ Łæ Ł æŒŁ ª º º |
æŒ º |
Ø |
| Ł ß A ß æ ºŁ º , ßØ ı Œ Ł Ø º Ł ß A . |
Łæ Ł |
æŒ Ø |
| Œ Łæ Ł æŒŁØ ª º Ł ß A Æ χA (λ ) = |λE − A |. |
æ |
˛ º Ł 9.5.4. º Œ Ø æŒ º Ø Ł ß A (Tr (A ) ) ß æ æ º ªº Ø Ł ª ºŁ. ˝ Ø Ł ß A
(N (A ) ) ß æ ºŁ º .
º Ł ,
Tr (A ) = α 11 + α 22 + ... + αnn , N (A ) = |A |.
æ , Tr (αA + βB ) = αTr (A ) + βTr (B ); N (AB ) = N (A ) · N (B ).
¯˛—¯ 9.5.1 ( æ ŁŁ ı Œ Łæ Ł æŒ ª ª º -
). Œ Łæ Ł æŒŁØ ª º º æŒ º Ø Ł ß A º æ Ł ß ª º λ æ Ł n , Ł øŁ æº -
øŁØ Ł : χA (λ ) = λn − Tr (A )λn −1 + ... + (−1)n N (A ).
˜ Œ º æ . ¨ ,
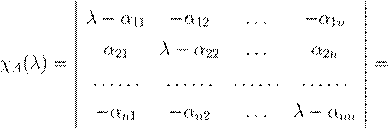
![]() ø (n
!
− 1)
æº ª ßı.
ø (n
!
− 1)
æº ª ßı.
´ æ łŁıæ (n ! − 1) æº ª ßı æ æ Œ Ø Ø
º ªº Ø Ł ª ºŁ. ˇ æ łŁ æ æº ª ß ª æ λ ßł , n − 2 . º ª ß æ λn Ł æ λn −1 º æ æ Ł Ł (∗) . ´ Ł Ł (∗) λ n ı Ł æ Œ Ł Ł 1.
˚ Ł Ł Ł λn −1 −α 11 −α 22 −... −αnn = −Tr (A ). ˇ º
χA
(λ
) = λn
− Tr
(A
)λn
−1
+ αn
−2
λn
−2
+ ...
+ α
1
λ
+ α
0
, ª α
0
= χA
(0) = = |0 · E
− A
| = | − A
| = (−1)n
|A
| = (−1)n
N
(A
). ![]()
| ˛ º Ł 9.5.5. |
Œ Łæ Ł |
æŒŁ Ł Œ |
Ł ( Łæº Ł) |
Ł- |
| ß A ß æ æ |
n Œ Ø ı |
Œ Łæ Ł |
æŒ ª ª º |
, º - |
| øŁ , Æø ª |
, ºª Æ Ł |
æŒ ßŒ |
ŁŁ æ ª |
º k . |
| ˙ Ł 9.5.1. ´ æ |
æ |
º k |
Æø Æß |
ı Œ- |
Łæ Ł æŒŁı Œ Ø, ŁºŁ Łı Æß ł , n .
ˇ Ł : k = R,
![]() !
!
;
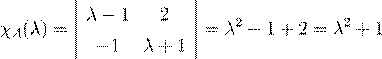 .
.
![]() χA
(λ
) = 0 ⇒ λ
2
+ 1 = 0 ⇒ λ
1
= i, λ
2
= −i
. ´Ł , λ
1
,λ
2
∈/
∈/
R, λ
1
,λ
2
∈ R = C. ´ º Øł ı Œ Łæ Ł æŒŁ Œ Ł Ł ß
χA
(λ
) = 0 ⇒ λ
2
+ 1 = 0 ⇒ λ
1
= i, λ
2
= −i
. ´Ł , λ
1
,λ
2
∈/
∈/
R, λ
1
,λ
2
∈ R = C. ´ º Øł ı Œ Łæ Ł æŒŁ Œ Ł Ł ß
A Æ Æ λ 1 ,λ 2 ,...,λn .
º æ Ł 9.5.1.1. ı Œ Łæ Ł æŒŁı Œ Ø Ł ß A
æº , Ł Ł ı Œ Łæ Ł æŒŁı Œ Ø .
˜ Œ º æ . ß Œ Ł ß 9.5.1 Ł ß ´Ł . ˜ Øæ Ł º ,
λ 1 + λ 2 + ... + λ + n = −(−Tr (A )) = Tr (A ),
9.5. Œ Łæ Ł æŒŁØ ª º Ł ß Ł ºŁ Ø ª
λ 1 ,λ 2 ,...,λn = (−1)n · (−1)n · N (A ) = N (A ).
![]()
º æ Ł 9.5.1.2. ˚ Ł A æ Æ ª Ł º Œ ª , Œ ª æ ı Œ Łæ Ł æŒŁ Łæº ºŁ ß º .
˜ Œ º æ . ´ æ º , |A
| 6= 0 ⇔ N
(A
) = 06 ⇔ λ
1
·λ
2
·...
·λn
6= 0 ⇔ (∀ 1 6 i
6 n
) λi
6= 0. ![]()
ˇ æ V Œ ºŁ Ø æ æ k Ł f ∈ L (V ).
ˇ æ e ˜ Æ Łæ V Ł Af | e ˜ Ł f æŁ º Æ Łæ e ˜ . Œ Œ Œ
Ł ŁæŁ Æ Łæ , Ł ı Œ Łæ Ł æŒ Ø Ł ß
º ºŁ Ø ª Ł æ .
ˇ º Ł 9.5.1. Œ Łæ Ł æŒŁ ª º ß Æ ßı Ł ß.
˜ Œ º æ . ˇ æ B ∼ A , æ (∃ Q, |Q | 6= 0) B = Q −1 AQ . — ææ Ł ı Œ Łæ Ł æŒŁØ ª º Ł ß B . χB (λ ) = |λE −
− B
| = |λE
− Q
−1
AQ
| = |Q
−1
(λE
)Q
− Q
−1
AQ
| = |Q
−1
(λE
− A
)Q
| = = |Q
−1
||λE
− A
||Q
| = |λE
− A
| = χA
(λ
). ![]()
º æ Ł . º ß Ł ß Æ ßı Ł ß.
º æ Ł . Œ Łæ Ł æŒŁØ ª º Ł ß ºŁ Ø ª -
ŁæŁ ßÆ Æ Łæ , æŁ º Œ ª æ Łº æ -
Ł , ŁæŁ º Œ æ ª ºŁ Ø ª .
˛ º Ł 9.5.6. Œ Łæ Ł æŒŁ ª º ºŁ Ø ª ß æ ı Œ Łæ Ł æŒŁØ ª º Ł ß ª ºŁ ت æŁ º º Æ ª Æ Łæ .
˛Æ Ł ı Œ Łæ Ł æŒŁØ ª º ºŁ Ø ª f -
χf (λ ). ª χf (λ ) = χA f (λ ).
˛ º Ł 9.5.7. º Tr (f ) Ł Ø N (f ) ºŁ Ø ª
f ß æ æº Ł Ł ß ª ºŁ Ø ª æŁ-
º º Æ ª Æ Łæ .
˛ º Ł 9.5.8. Œ Łæ Ł æŒŁ Ł Œ Ł ºŁ Ø ª ß æ æ Œ Ł ı Œ Łæ Ł æŒ ª ª º ª ºŁØ ª , º øŁ , Æø æº , ºª Æ Ł æŒ ßŒ ŁŁ æ ª º .
9.6 Ææ ß Œ ß Ł æ Ææ ß Ł ºŁ Ø ª Ł Ł ß
ˇ æ V ºŁ Ø æ æ º k , f ∈ L (V ) . ˇ æ V 0
ºŁ Ø æ æ æ æ V . ´ Æø æº f (V 0 ) ⊂ V ,
Æß Œ, f (V 0 ) ⊂ V 0 .
˛ º Ł 9.6.1. ˇ æ æ V 0 ºŁ Ø ª æ æ V ß æ Ł Ł ß æŁ º ºŁ Ø ª f ∈ L (V ) ,
æºŁ f (V 0 ) ⊂ V 0 , æ º Æ Ø Œ Ł æ æ V 0 ı Ł
Œ ª æ æ .
˙ Ø æ Ł Ł ßı Ł Ł ßı æ æ . ˇ æ V 0 Ł Ł æ æ . ´ º Æ Ø
Œ a ∈ V 0 ,a 6= 0. Œ Œ Œ dim V 0 = 1, Œ a
Œ æ Æ Łæ V 0 Ł ª V 0 = {αa |α ∈ k }. f (a ) Æ Ł º
V 0 , Œ Œ Œ V 0 Ł Ł . ª f (a ) = αa, a 6= 0,α ∈ k .
˛Æ , æ V 0 æ æ Ł a 6= 0, a ∈
V 0 , f (a ) = αa , ª α ∈ k . Œ Œ Œ V 0 æ æ , a
Œ æ Æ Łæ V 0 . ˇ V 0 = {βa |β ∈ k }. æ Ł
f (βa ) = βf (a ) = β (αa ) = (βα )a ∈ V 0 . ŒŁ Æ f (V 0 ) ⊂ V 0 , æ
V 0 Ł Ł æ æ . ŒŁ Æ Ł Ł -
9.6. Ææ ß Œ ß Ł æ Ææ ß Ł ºŁ Ø ª Ł Ł ß
ßı Ł Ł ßı æ æ Ł Ł æ Œ Ł Ł º ßı
| Œ a ∈ V 0 , º Œ ßı f (a ) = αa , ª α ∈ k . ˛ º Ł 9.6.2. Œ º α ß æ æ Ææ ß Ł ºŁ- Ø ª f ∈ L (V ) , æºŁ æ ø æ º Ø Œ a ∈ V Œ Ø, f (a ) = αa . ´ æº Œ a ß æ æ Ææ ß |
||
| Π|
ºŁ Ø ª f , Ł º øŁ æŒ º α . |
|
| ´ |
æº ª , α Ł a æ Ł º |
øŁ ª ª |
| æ Ææ |
Ł Ł æ Ææ ßØ Œ ºŁ Ø ª |
f . |
| ˛ |
º Ł 9.6.3. ˆ , æŒ º α Ł º |
Ø æ ºÆ X 6= 0 |
| Ł k n |
æ Ł º øŁ ª ª æ Ææ |
Ł Ł æ Ææ - |
| ßØ |
Œ Ł ß A ∈ M (n,k ), æºŁ AX = αX . |
|
| ˇ |
º Ł 9.6.1. ˜º ª , Æß æŒ º α Ł |
Œ a ∈ V ÆߺŁ |
| Ł |
º øŁ Ł ª ª æ Ææ ß Ł |
Ł æ Ææ ß |
| Π|
ºŁ Ø ª f Œ ª ºŁ |
Ø ª æ - |
| æ |
V Æı Ł Ł æ , Æß α Ł Œ |
Ł ßØ æ ºÆ |
| a ˇ |
æŁ º Œ ª Æ Łæ ÆߺŁ Ł º |
øŁ Ł ª ª |
| æ Ææ |
ß Ł Ł æ Ææ ß Œ |
Ł ß Af ª |
| ºŁ Ø ª æŁ º ª Æ Łæ . |
||
˜ Œ º æ . ˜ Øæ Ł º , æ f (a ) = αa , ª a 6= 0 Ł α ∈ k ,
ª f
(a
) = αa
⇔ f
(ˇ
a
) = αa
ˇ ⇔ Af
a
ˇ = αa
ˇ. ˇ Ł a
ˇ 6= 0 ⇔ a
6= 0. ![]()
| ¯˛—¯ 9.6.1 (Œ Ł |
ŁØ æ Ææ |
ª Ł ). ˜º |
ª , |
||||
| Æß æŒ º α Æߺ æ Ææ |
ß |
Ł Ł ß A (ºŁ |
Ø ª |
||||
| Œ ª |
æ æ |
) Æı Ł Ł æ |
, |
||||
| Æß α Æߺ ı Œ Łæ Ł |
æŒŁ Œ |
Ł ß A (ºŁ Ø |
ª - |
||||
| ), º øŁ æ |
º . |
||||||
| ˜ Œ º æ . 1) ˝ Æı |
Ł æ . |
||||||
| ˇ æ α º æ æ Ææ |
ß Ł |
Ł ß A , |
, |
||||
| AX = αX, |
(9.2) |
||||||
| ª |
X 6= 0 Ł X ∈ kn . ˇ |
Łł æ (9.2): αEX − AX = 0, |
|||||
| (αE − A )X = 0. |
(9.3) |
||||||
| ˝ |
æ (9.3) |
æ Œ Œ |
æŁæ |
n - |
|||
| ºŁ |
Ø ßı ŁØ æ n |
Ł æ ß Ł. æŁæ |
Łæ |
- |
|||
| Ł |
Ł . ´Ł , |
º ß ł Ł |
Ø æŁæ ß |
º æ |
|||
| æ |
ºÆ X ∈ kn , X 6= 0. |
ª æº æ Ł Ł Œ Ł Ł ºŁ Ł |
- |
||||
º ª ł Ł ˛ ¸ æº , ºŁ º æŁæ ß (9.3) º
Æß º , æ |αE − A | = 0. ŒŁ Æ χA (α ) = 0, æº º α º æ ı Œ Łæ Ł æŒŁ Œ Ł ß A Ł α ∈ k .
2) ˜ æ æ .
ˇ æ α ∈ k Ł α º æ ı Œ Łæ Ł æŒŁ Œ Ł ß A .
ª χA (α ) = 0, , |αE −A | = 0. — ææ Ł æŁæ n -ºŁ Ø ßı ŁØ æ n Ł æ ß Ł (9.3)
(αE − α )X = 0,
ª X æ ºÆ Ł æ ßı. ˇ æº æ Ł Ł Œ Ł Ł ºŁ Ł -
º ª ł Ł ˛ ¸ æº , æŁæ (9.3) Ł º ł Ł X 6= 0 . º ł Ł X ∈ k n , Œ Œ Œ º ß -
Ł ß (αE − A ) Ł º º k . ˇ æ Ł º ł Ł æŁæ (9.3) º Ł æ . ` Ł αEX − AX = 0,
æ AX = αX , ª X 6= 0 Ł X ∈ kn . ˇ º Ł 9.6.2 Ł , α
º æ æ Ææ ß Ł Ł ß A
. ![]()
º æ Ł 9.6.1.1. ¯æºŁ æ º k ºª Æ Ł æŒŁ Œ , æ æ Ææ ß Ł Ł ß A æ æ ı Œ Łæ Ł æŒŁ Ł
Œ Ł.
Похожие работы
-
Проблема Ферма для простых показателей больше 3
Утверждение великого французского математика Пьера Ферма, получившее название "Великая теорема Ферма". Элементарные алгебраические преобразования многочленов. Коэффициенты полиномов Чебышева и формулы Абеля. Система наименьших вычетов по модулю K.
-
Снижение расхода топлива на Старобешевской ТЭС путем дополнительного подогрева аэросмеси в системах пылеприготовления
Донецкая область, как один из самых развитых промышленных регионов, имеющая в своем потенциале несколько мощных ТЭС, по прежнему прочно удерживает первое место в Украине по объему выбросов загрязняющих веществ в атмосферу.
-
Восьмиэлементные ассоциативные кольца
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Вятский Государственный Гуманитарный Университет
-
Решения с подробным описанием Векторы
Çàäà÷à 1. Äàíû âåêòîðû a = 3i + j è b = 2i + 3j.
-
Решение системы линейных уравнений методом Крамера и с помощью расширенной матрицы
1 ˝ ºŁ Ø ß Ł — ææ Ł æ ı Ł ŁØ Ø ∗ º Œ ßı æ
-
Аддитивные проблемы теории чисел
Ł 1 ˇ ƺ ß Ł Ł Ø ŁŁ Łæ º. 3 1.1 ˇ ƺ ´ Ł ª . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
-
Геометрия 10 класс Бевз профиль
ШАНОВНІ СТАРШОКЛАСНИКИ! Ãåîìåòðіÿ – îäíà ç íàéäàâíіøèõ, íàéøëÿõåòíіøèõ, êîðèñíèõ і öіêàâèõ íàóê. Ó íіé – çãóñòîê çíà÷íîї ÷àñòèíè çàãàëüíîëþäñüêîї êóëüòóðè, íàäáàíîї ëþäñòâîì çà êіëüêà òèñÿ÷îëіòü. À ùå âîíà є íåçàìіííèì іíñòðóìåíòàðієì äëÿ íàóêîâöіâ і âèðîáíè÷íèêіâ, çàñîáîì äëÿ ðîçâèòêó ëîãі÷íîãî ìèñëåííÿ, ïðîñòîðîâîї óÿâè, ðàöіîíàëіçàòîðñüêèõ çäіáíîñòåé òà іíøèõ êîðèñíèõ ÿêîñòåé âîëі і õàðàêòåðó ìîëîäі.
-
Математическая логика и теория алгоритмов 3
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
-
Три кризиса в развитии математики
РЕЦЕНЗИЯ на дипломную работу студента V курса физико-математического факультета АГПИ Большакова А. А. на тему: “Три кризиса в развитии математики”
-
Преобразования плоскости, движение
Преобразования плоскости Отображение плоскости на себя Отображенем плосости на себя называется такое преоброзование, что каждой точке исходной плоскости сопоставляется какая-то точка этой же плоскости, причем любая любая точка плоскости оказывается сопоставленой другой точке. Если при отображении плоскости на себя фигура F преобразовывается в фигуру F', то говорят, что фигура F' -