Referat.me
/ / Решение системы линейных уравнений методом Крамера и с помощью расширенной матрицы

Название: Решение системы линейных уравнений методом Крамера и с помощью расширенной матрицы

Вид работы: реферат

Рубрика: Математика

Размер файла: 144.6 Kb

Скачать файл: referat.me-218350.pdf

Краткое описание работы: 1 ˝ ºŁ Ø ß Ł — ææ Ł æ ı Ł ŁØ Ø ∗ º Œ ßı æ

Решение системы линейных уравнений методом Крамера и с помощью расширенной матрицы

1 ˝ ºŁ Ø ß Ł

— ææ

Ł

æ

ı

Ł

ŁØ

Ø x = x ∗ ,

º

Œ

ßı æ

ºŁ

æ

f (x ) = 0.

(1)

´ ŁŁŁ f (x ) - Œ ºŁ Ø Œ Ł x .

¯æºŁ ŒŁ Ł æ ø æ , Ł ß æ Œ Ł -

Ł (1). ˚ ß æ æ ß , æºŁ f 0 (x ∗ ) 6= 0 Ł Œ ß , æºŁ f (k ) (x ∗ ) = 0 º k = 1,...,n − 1, f (n ) (x ∗ ) 6= 0. º n ß æ Œ æ Œ .

1.1 ˛ º Ł Œ Ø

ˇ º Ł Œ Ø Ł (1) Ł º Ł æ -

Œ ª Ł º (a,b ), Œ º Ł Œ Ł . ˛æ Ø º Ł Œ Ø æº Ł

[1] . ˇ æ Œ Ł º Ł ß Œ -

Œ [a,b ], Œ ı Œ ª Ł Ł Ł ßı Œ .

ª a Ł b Ø æ ı Æß Œ c , Œ Ø Œ Ł Æ ø æ º :

f (c ) = 0, a < c < b.

¯æºŁ Œ Ł f (x ) Ł º , Ł ª º Ł

º Œ Ł Œ Ł f (x ) = 0 .

ºª Ł º Ł ºŁ æº øŁ Æ

YesDo:=True; While YesDo do

Input a,b, M ; h = (b − a )/M ; fmin := 1. 0e 20; xi := a ; fi := f (a ); for i:=1 to M do begin {i }

x i −1 := x i ; f i −1 := f i ; xi := a + h ∗ i ; fi := f (xi ); If fi < fmin Then begin {min }

f min := f i ; x min := x i ; end; {min } If fi −1 ∗ fi ≤ 0 Then

Output x i −1,f i −1, x i ,f i ; end; {i }

Output f min ,x min ; Input YesDo; end; {While }

1.2 ÆŁæ Œ ŁØ ÆŁæ Œ ŁØ( º Ł º ) æ æº ø Ł -

Ł ææ : Ł º a,b , Œ (fa = f (a )) · (fb = f (b )) < 0,

ºŁ æ º - xs = (a +b )/ 2 Ł ß Łæº æ fs = f (xs ). ¯æºŁ fs ·f (a ) ≥ 0, a := xs , fa := fs , Ł b := xs , fb := fs ; ˜ º ß º æ æº øŁØ ł ª, Ł . .

˝ i- ł ª ŁÆºŁ ß Ł Œ æº Ł º æ (a +b )/ 2,

Œ Ø ª ł æ Ł - º æ (b − a )/ 2.

ÆŁæ Œ ŁØ Łæ æº øŁ ºª Ł [2]

1: Input a,b, δ,N ;

2: i := 0;

3: fa := f (a ); fb := f (b );

4: Repeat

5: xs := (a + b )/ 2; fs := f (xs );;

6: If fs ∗ fa ≥ 0

7: Then begin fa := fs ; a := xs end;

8: Else begin fb := fs ; b := xs end;

9: i := i + 1;

10: xi := (a + b )/ 2;

11: dx := (b − a )/ 2;

12: Until ((|dx | ≤ δ |xi |) OR (i ≥ N ));

13: Output i,xi ,dx ;

1.3 ı

´ ı æ º Ł Œ (a,b ) º Łæ º æ ºŁØ Ł º Ł ª Ł ßı ŁØ Œ ŁŁ f (x )

f ˆ(t ) = f (a )(1 − t ) + f (b )t, 0 ≤ t = (x − a )/ (b − a ) ≤ 1.

º ø Œ º Œ ı Ł æ Ł Ł f ˆ (t ) = 0:

t ∗ = f (a )/ (f (a ) − f (b )), xs = a + t ∗ (b − a );

˜ º Łæı Ł æ Łª ª Ł Ł º Œ , Œ Œ ÆŁæ Œ ŁØ. ı Łæ æº øŁ ºª Ł

1: Input a,b, δ,N ;

2: fa := f (a ); fb := f (b );

3: i := 0;

4: fa := f (a ); fb := f (b );

5: Repeat

6: y := x 2 − x 1;

7: t := fa/ (fa − fb ); xs := a + y ∗ t

8: fs := f (xs );;

9: If fs ∗ fa ≥ 0

10: Then begin fa := fs ; a := xs end;

11: Else begin fb := fs ; b := xs end;

12: i := i + 1;

13: xi := (a + b )/ 2;

14: dx := (b − a )/ 2;

15: Until ((|dx | ≤ δ |xi |) OR (i ≥ N ));

16: Output i,xi ,dx ;

ÆŁæ Œ ŁØ Ł

ı

º

Łæ

º

ª

æº

!

1.4 æ º Ł

¨ ª æ æ Ł ı ºŁ Ø ª Ł (1) Œ

Æߌ Ł Ł º Ł

dx/dt = f (x ), x (0) = x 0 . (2)

Ł º ƺ æ Ø Ł ß º ß æ Ł ß æ æ Ł , Æß Ł t → ∞ x (t ) → x ∗ . ª ŁÆºŁ ł Ł

ŁŁ (2) æ ø æ Ø Ł ª Łæº ª ( º -

æ

Æ º łŁı t ) ı ł ŁÆºŁ Ł Œ ł Ł

(1).

ˇ

æ ØłŁ ºª Ł Æ Øº , º

øŁØæ

Ł

æ

Ø Ł ŁŁ

xi +1 = xi + τf (xi ).

(3)

æ

º Ł Łæ æº øŁ ºª

Ł

1:

Input

x 0 , τ , δ, N ;

2:

i := 0;

3:

Repeat

4:

dx = τ ∗ f (xi );

5:

i := i + 1;

6:

xi := xi + dx ;

7:

Until ((|dx | ≤ δ |xi |) OR (i ≥ N ));

8:

Output

i,xi ,dx ;

˜º

ª ł

æ Ł ²k = xk − x ∗ Ł (3) º æ æº

²k +1 = ²k + τ (f (xk ) − f (x ∗ )).

ø

Ł

ˇ

æ Ł

f (xk ) − f (x ∗ ) = f 0 (x ˜)²k , º Ł æ ł

²k +1 = (1 + τf 0 (x ˜))²k ,

Ł

Ł Œ ª æº , º æı Ł æ Ł æ

º Ł º ß

ß º æ æº øŁ æº Ł : æº º æ {xk ,k = 0, 1,... }º ı Ł æ ƺ æ Ł |xk −x ∗ | < R , Œ Ø Ł ª Ł-

Ł æ ı æ Ø Œ. ª ßÆ τ , º ø ª

æº Ł ,

sign (τ ) = −sign (f 0 ), |τ | < 2/ max|f 0 |,

Æ æ Ł æı Ł æ æ º Ł .

1.5 ˝

˝ º Ł (1) Łæß æ Ł

xi +1 = xi − [df/dx ]−1 f (xi ). (4)

˛ º Ł :

ª , Œ Ł g (x ) ∈ Lipc (X ) , æºŁ |g (x ) − g (y )| ≤ c |x − y | º æ ı (x,y ) ∈ X .

( æı Ł æ Ł ˝ ). ˇ æ f : D → R ª D - Œ ß ßØ Ł º , R - ø æ æ ,

Ł æ f 0 ∈ Lipc (D ). ˇ º Ł , º Œ ª ρ > 0 |f 0 | ≥ ρ Ł æ ı x ∈ D . ¯æºŁ Ł f (x ) = 0 Ł ł Ł , æ ø æ

Œ η > 0, Œ , æºŁ |x 0 − x ∗ | < η , æº º æ , º Ø

xk +1 = xk − f (xk )/f 0 (xk ), k = 0, 1, 2,...,

æ ø æ Ł æı Ł æ Œ x ∗ . ` º ª , º k = 0, 1, 2,...

.

˙ Ł 1. ˚ Œ æº Ł ß, Ł f 0 (x ∗ ) = 06 æı Ł æ Œ Ł . ¯æºŁ f 0 (x ∗ ) = 0 , º Œ ºŁ Ø .

˙ Ł 2. ˜º æı Ł æ Ł ˝ º ŁÆºŁ Ł x 0 º Æß æ ƺŁ Œ Œ Œ . ¯æºŁ ææ Ł |x 0 −x ∗ |

ºŁŒ , ˝ Æø æı Ł æ . ˝ ºŁ æº øŁ ºª Ł

1: Input x 0 , δ, N ;

2: i := 0; 3: Repeat

4: df := [df/dx ](xi );

5: dx = f (xi )/df ;

6: i := i + 1;

7: xi := xi − dx ;

8: Until ((|dx | ≤ δ |xi |) OR (i ≥ N )); 9: Output

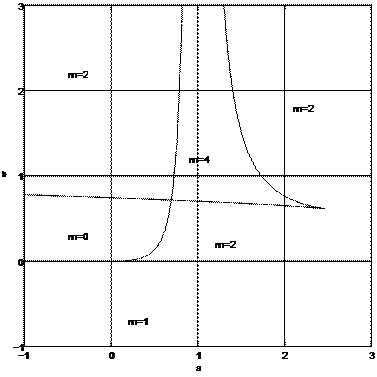
—Łæ. 1: — ÆŁ

Ł º æŒ æ Ł Ł

ex − a − bx 3 = 0

1.6 æ

Ł

1. ´ Œ æ 1-ª

æ ª Łæ º æ Ł

f (x ) = exp(x ) − a − bx 3 = 0.

(5)

´ ŁæŁ æ Ł

ŁØ a,b

Ł Ł

m = 0, 1, 2, 4 Œ

. ˜º Łææº Ł Œ 1-Ø

Ł Ø Œ ŁŁ

f (x ) º ı

Ł Œ Ł Ł

g (x ) = f 0 (x ) = exp(x ) − 3bx 2 = 0. (6)

˝ Łæ Œ 1 Œ ÆŁ Ł º æŒ æ Ł a,b ƺ æ Ł æ ºŁ ß Łæº Œ Ø Ł (5).

2. ´ Œ æ 2-ª æ ª Łæ º æ Ł

f (x ) = exp(−1/ (x − 1)2 ) = 0. (7)

Ł Ł Ł æ ßØ Œ x ∗ = 1 Æ æŒ Ø Œ æ Ł( f (k ) (1) = 0, k = 0, 1,... ). ˇ Ł f 0 (x ) < 0 º x < 1 Ł f 0 (x ) > 0 º x > 1 .

1.7 ˚ ß Œæ Ł ß

1. ˜º Œ ŁŁ Ł (5) æ Ł a = 1. 15,b = 1. 25 Ø Ł

ª Ł ß Œ Ø. ˜º Œ ŁŁ Ł (6) æ b = 1. 25 ØŁ ª Ł ß Œ Ø Ł ŒŁ æ Ø ø æ Ø æŁ.

˚ º Ł Ł :

Œ Ł f (x ): Œ Ł( ŁÆºŁ )

x 1 = −0. 83, x 2 = 0. 14, x 3 = 1. 20, x 4 = 5. 14

Œ Ł g (x ) = f 0 (x ): ŒŁ Ł Œ Ł

(−... −) − 0. 41 (+... +) 0. 75 (−... −) 4. 18 (+... +)

2. ˛ Łæ ß Ł ßł Ł(ÆŁæ Œ ŁØ, ı , æ º Ł , ˝ -

) º ŁØ δ = 1. 0e − 2, 1. 0e − 3, 1. 0e − 4, 1. 0e − 5 Ø Ł Œ Ł Œ ŁŁ (5)æ Ł Ł a = 1. 15,b = 1. 25. ˜º Łı Œ Ø æ æ Ł ƺŁ ß ŁæŁ æ Ł Łæº Ł ŁØ δ .

3. æ º Ł ß æ Ø Ł Œ Œ ŁŁ (5), Æ Ł τ , º Œ ßı æı Ł æ Ł. ˚ ŒŁ Æ º æ æı Ł æ Ł Ł ª ææ ?

4. ˝ :

æº Œ Œ æ Ł 2 ˝ æı Ł æ ºŁ Ø , . .æ ø æ

º , æº æ ª Œ . ˇ Ł , Æ ºŁ Ł ŁŁ ßØ ˝

xi +1 = xi − 2[df/dx ]−1 f (xi )

Ł º Œ Œ æ Ł 2 æŒ æ æı Ł æ Ł, Ł æ ßØ º æ ª Œ . ˜º ŒŁ Łæ º Ł

h (x ) = sin((x − 1)2 ) = 0.

˜º Ł δ = 1. 0e − 7 Ø Ł Œ ª Ł æ ß Ł Ł Ł Ł ß ˝ . Ł Łæº Ł ŁØ.


[1] 1ˇ ` º -˚ łŁ

[2] 2´ Ł Ł ßı Ł ºª Ł ı Łæ º æ º Œ æ Ł Ł ŁØ. ˝ -

Łı Ł Ł Ł , Łæ º æ Œ ß Ł غ it_gen.pdf

Похожие работы

  • Решения с подробным описанием Векторы

    Çàäà÷à 1. Äàíû âåêòîðû a = 3i + j è b = 2i + 3j.

  • Аддитивные проблемы теории чисел

    Ł 1 ˇ ƺ ß Ł Ł Ø ŁŁ Łæ º. 3 1.1 ˇ ƺ ´ Ł ª . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

  • Геометрия 10 класс Бевз профиль

    ШАНОВНІ СТАРШОКЛАСНИКИ! Ãåîìåòðіÿ – îäíà ç íàéäàâíіøèõ, íàéøëÿõåòíіøèõ, êîðèñíèõ і öіêàâèõ íàóê. Ó íіé – çãóñòîê çíà÷íîї ÷àñòèíè çàãàëüíîëþäñüêîї êóëüòóðè, íàäáàíîї ëþäñòâîì çà êіëüêà òèñÿ÷îëіòü. À ùå âîíà є íåçàìіííèì іíñòðóìåíòàðієì äëÿ íàóêîâöіâ і âèðîáíè÷íèêіâ, çàñîáîì äëÿ ðîçâèòêó ëîãі÷íîãî ìèñëåííÿ, ïðîñòîðîâîї óÿâè, ðàöіîíàëіçàòîðñüêèõ çäіáíîñòåé òà іíøèõ êîðèñíèõ ÿêîñòåé âîëі і õàðàêòåðó ìîëîäі.

  • Математическая логика и теория алгоритмов 3

    МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

  • Антье и ее окружение

    Антье и ее свойства. Графики антье.

  • Три кризиса в развитии математики

    РЕЦЕНЗИЯ на дипломную работу студента V курса физико-математического факультета АГПИ Большакова А. А. на тему: “Три кризиса в развитии математики”

  • Преобразования плоскости, движение

    Преобразования плоскости Отображение плоскости на себя Отображенем плосости на себя называется такое преоброзование, что каждой точке исходной плоскости сопоставляется какая-то точка этой же плоскости, причем любая любая точка плоскости оказывается сопоставленой другой точке. Если при отображении плоскости на себя фигура F преобразовывается в фигуру F', то говорят, что фигура F' -

  • Алгебра

    ˛˜¯—˘ ˝¨¯ 6 ª º ß 3 6.1 ˚ º ª º . . . . . . . . . . . . . . . . . . . . . . 3 6.2 º ŁŁ æ æ Œ . ` . ı ˆ 6

  • Задачи по Высшей математике

    Вариант № 2 Задача 1 Найти объединение и пересечение множеств А и В, если А ={1;3;5} и B={0;1;2;-3;4;-5}. Решение: Объединение множеств А и В А  В= {0;1;2;3;5;-3;4;-5},

  • Системы линейных уравнений

    Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.