Название: Математические модели электромеханических систем в пространстве состояний
Вид работы: реферат
Рубрика: Математика
Размер файла: 49.84 Kb
Скачать файл: referat.me-216933.docx
Краткое описание работы: Способы получения уравнений состояния реальных физических объектов ничем не отличаются от способов описания этих объектов с помощью дифференциальных уравнений. Уравнения состояния записываются на основе физических законов, положенных в основу работы объекта.
Математические модели электромеханических систем в пространстве состояний
2. Математические модели электромеханических систем в пространстве состояний
Способы получения уравнений состояния реальных физических объектов ничем не отличаются от способов описания этих объектов с помощью дифференциальных уравнений. Уравнения состояния записываются на основе физических законов, положенных в основу работы объекта.
Рассмотрим электромеханическую систему, состоящую из двигателя постоянного тока с независимым возбуждением, работающего на инерционную нагрузку с вязким трением. Управляющим воздействием для двигателя считаем напряжение на якоре U(t), выходной координатой, угол поворота вала двигателя y(t)=j(t). Уравнение электрической цепи имеет вид
![]() ,
,
где ![]() - противо ЭДС,
- противо ЭДС, ![]() - угловая скорость вала двигателя,
- угловая скорость вала двигателя, ![]() - единый электромагнитный коэффициент.
- единый электромагнитный коэффициент.
Уравнение моментов будет иметь следующий вид
![]() ,
,
где ![]() , J - момент инерции нагрузки, приведенный к валу двигателя, f - коэффициент вязкого трения.
, J - момент инерции нагрузки, приведенный к валу двигателя, f - коэффициент вязкого трения.
Выберем следующие переменные состояния: х1 =i, x2 =w, x3 =j.
Получим
![]() ,
,
![]() .
.
Запишем эти уравнения относительно переменных ![]() ,
, ![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Запишем матричные уравнения
![]() ,
,
![]() ,
,
где
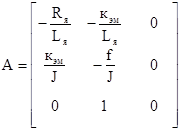 ,
, 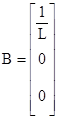 ,
, ![]() .
.
Рассмотрим структурную схему электромеханической системы с двигателем постоянного тока, работающего на инерционную нагрузку с вязким трением.
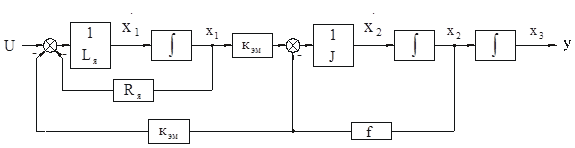
Рис. 2.1. Структурная схема электромеханической системы с двигателем постоянного тока
Запишем уравнение состояния для механической системы, представляющей собой груз массой m, подвешенный на пружине и соединенный с гидравлическим демпфером. К грузу приложена сила P(t), выходная переменная перемещения x(t), управляющие воздействия U(t)=P(t). Уравнение движения груза получаем из уравнения равновесия сил
![]() ,
,
где ![]() - инерционная сила, f - коэффициент вязкого трения,
- инерционная сила, f - коэффициент вязкого трения, ![]() - сила сопротивления демпфера,
- сила сопротивления демпфера, ![]() - сила сопротивления пружины.
- сила сопротивления пружины.
Выбираем в качестве переменных состояния x(t) и ![]() - перемещение и скорость перемещения соответственно.
- перемещение и скорость перемещения соответственно.
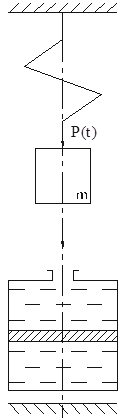
Рис. 2.2. Механическая система, включающая в своем составе пружину, массу и вязкий демпфер
Так как дифференциальное уравнение имеет второй порядок, то и количество переменных состояния будет равно двум. Исходное уравнение движения груза можно записать в виде двух уравнений
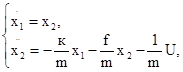
где U(t)=P(t) - управляющее воздействие.
Добавим к этим уравнениям следующее уравнение выхода
![]() .
.
Эти уравнения представляют собой уравнения состояния приведенной механической системы. Запишем эти уравнения состояния в матричном виде
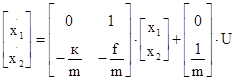 ,
,
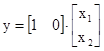 .
.
Запишем это уравнение в другом виде
![]() ,
,
![]() ,
,
где 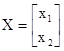 ,
, 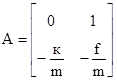 ,
, 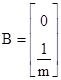 ,
, ![]() ,
, ![]() .
.
С данным уравнением состояния можно сопоставлять следующую структурную схему, где двойными линиями показаны векторные переменные.
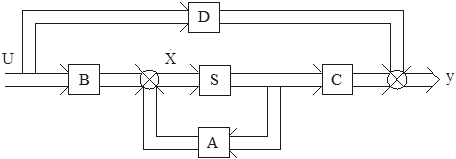
Рис. 2.3. Структурная схема
Пример: Рассмотрим электрическую цепь и получим уравнение состояния RLC цепи
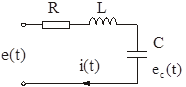
Рис. 2.4. RLC цепь
Динамическое поведение этой электрической системы полностью определяется при t³t0 , если известны начальные значения: i(t0 ), ec (t0 ) и входное напряжение e(t) при t³t0 , следовательно, эта система полностью определяется переменными состояния i(t) и ec (t). При указанных переменных состояния i(t) и ec (t) имеем следующие уравнения
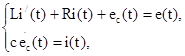
где ![]() ,
, ![]() .
.
Введем следующие обозначения
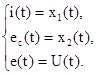
В соответствии с этими обозначениями получаем
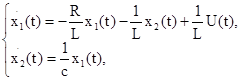
причем ![]() .
.
Следовательно, для электрической цепи запишем эту систему в векторно-матричном виде
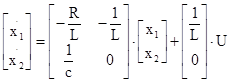 ,
,
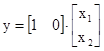 .
.
Запишем матричные уравнения
![]() ,
,
![]() ,
,
где 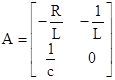 ,
, 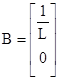 ,
, ![]() ,
, ![]() .
.
Похожие работы
-
Имитационная модель системы автоматизированного проектирования абстрактного этапа реализации устройств управления
Для дискретных систем управления интерпретируемых конечными автоматами предложена система их проектирования в виде параллельно функционирующих стандартных компонентных автоматов.
-
Ультразвук и измерения дальности
Ультразвук (УЗ) – упругие колебания и волны, частота которых превышает 15 – 20 кГц. Нижняя граница области УЗ-вых частот, отделяющая ее от области слышимого звука, определяется субъективными свойствами человеческого слуха и является условной.
-
Исследование изменения технического состояния систем при их эксплуатации
При эксплуатации любой технической системы происходит взаимодействие ее элементов между собой, а также с рабочей и окружающей средой. Такое взаимодействие приводит к изменению геометрические параметров элементов.
-
Математическая модель системы в переменных пространства состояний
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ В ПЕРЕМЕННЫХ ПРОСТРАНСТВА СОСТОЯНИЙ ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ Математическая модель системы в переменных пространства состояний имеет вид
-
Замечательное уравнение кинематики
В предлагаемой статье рассмотрена возможность расширения сферы применения кинематических уравнений для решения задач механики. Показана возможность переноса метода составления простейших уравнений движения.
-
СМО с отказами
СМО с отказами (задача Эрланга) Рассматривается N-канальная СМО с отказами: λпотерь λобслуживания υ υ υ λ Любая заявка может быть обслужена любым свободным каналом. Если все каналы заняты, заявка немедленно получает отказ в обслуживании и покидает систему (теряется).
-
Методы подобия и моделирования с привлечением физических уравнений
Преобразования уравнений, нахождение соответствующих критериев подобия. Подобие стационарных и нестационарных физических полей. Масштабные преобразования алгебраических и дифференциальных уравнений. Моделирование задач с начальным и граничным условиями.
-
Дифференциальные уравнения линейных систем автоматического регулирования
Определение динамических свойств объектов с помощью дифференциальных уравнений для сравнительно простых объектов. Выражение входной и выходной величины элемента в долях, введение безразмерных координат. График кривой разгона, коэффициент усиления.
-
Математическая экономика
Понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономическим происхождением, интерпретацией и практическими приложениями. Особенно существенна связь с экономической наукой и практикой.
-
Математическое моделирование 2
Занятие 2 Содержание занятия: Математическое моделирование. 1 Классификация математических моделей. 2 Математические модели с сосредоточенными параметрами. 2