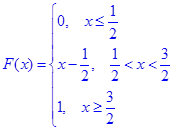Название: Решение задач по курсу теории вероятности и математической статистики

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 113.03 Kb

Скачать файл: referat.me-217632.docx

Краткое описание работы: Определение вероятности наступления определенного события по законам теории вероятности. Вычисление математического ожидания, дисперсии и среднего квадратичного отклонения. Нахождение выборочного уравнения регрессии по данным корреляционной таблицы.

Решение задач по курсу теории вероятности и математической статистики

Вариант 1

№ 1

Три стрелка делают по одному выстрелу по одной и той же цели. Вероятности поражения целей равны соответственно р₁ = 0,9, р₂ = 0,8, р₃ = 0,7.

Найти вероятности того, что:

а) все три стрелка попадают в цель;

б) только один из них попадает в цель;

в) хотя бы один стрелок попадает в цель.

Обозначим события: А – все 3 стрелка попадают в цель; В – только один стрелок попадает в цель; С – хотя бы один стрелок попадает в цель.

Вероятности промахов равны соответственно: q₁ = 0,1, q₂ = 0,2, q₃ = 0,3.

а) Р(А) = р₁ р₂ р₃ = 0,9∙0,8∙0,7 = 0,504.

б) Р(В) = p₁ q₂ q₃ + q₁ p₂ q₃ + q₁ q₂ p₃ = 0,9∙0,2∙0,3 + 0,1∙0,8∙0,3 + 0,1∙0,2∙0,7 = 0,092.

в) Событие – все три стрелка промахиваются. Тогда

Р(С) = 1 – Р() = 1 – 0,1∙0,2∙0,3 = 1 – 0,006 = 0,994.

№ 11

Вероятность наступления события в каждом из одинаковых независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит ровно 5 раз

У нас nдостаточно великó, р малó, λ = np = 150 ∙ 0,02 = 3 < 9, k = 5. Справедливо равенство Пуассона: . Таким образом,

№ 21

По данному закону распределения дискретной случайной величины Х определить математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение σ(Х).

хі	1	2	3	4	5
рі	0,05	0,18	0,23	0,41	0,13

Последовательно получаем:

₅

М(Х) = ∑ х_і р_і = 0,05 + 2∙0,18 + 3∙0,23 + 4∙0,41 + 5∙0,13 = 3,39.

i=1

₅

D(X) = ∑ x_i ²p_i – M² = 0,05 + 2²∙0,18 + 3²∙0,23 + 4²∙0,41 + 5²∙0,13 – 3,39² = i=1

1,1579.

σ(Х) = √D(X) = √1,1579 = 1,076.

№ 31

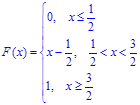
Случайная величина Х задана интегральной функцией

а) дифференциальную функцию f(x) (плотность вероятности);

б) математическое ожидание и дисперсию величины х;

в) вероятность того, что X примет значение, принадлежащее интервалу

;

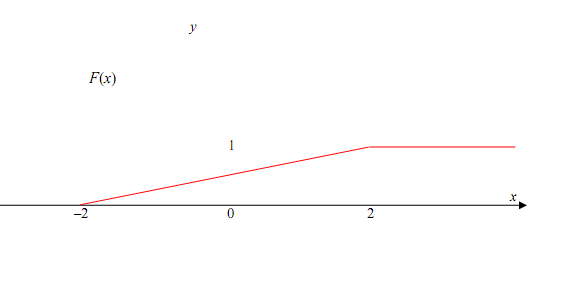
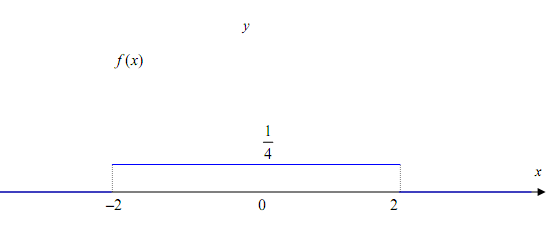
г) построить графики функций F(x) и f(x).

Последовательно получаем:

а) ;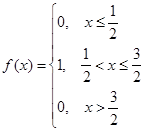

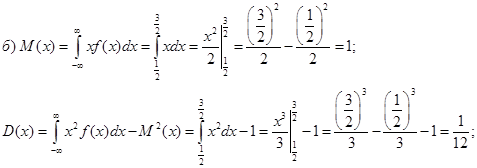
в) Р(a < x < b) = F(b) – F(a) ÞP= F(1) – F= – 0 = .

Графики функций поданы далее.

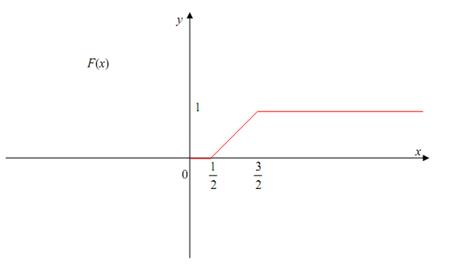
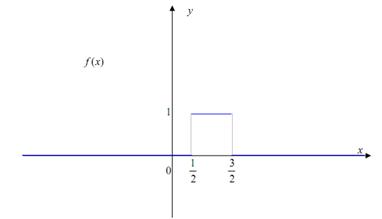
№ 41

Определить вероятность того, что нормально распределённая величина Х примет значение, принадлежащее интервалу (α; β) если известны математическое ожидание а и среднее квадратическое отклонение σ. Данные: α = 2; β = 13; а = 10; σ = 4.

Используем формулу Р(α < x < β) =

Имеем: Р(2 < x < 13) == Ф– Ф(–2).

Поскольку функция Лапласа есть нечетная, можем записать:

Ф– Ф(–2) = Ф+ Ф(2) = 0,2734 + 0,4772 = 0,7506.

№ 51

Поданному статистическому распределению выборки

хі	4	5,8	7,6	9,4	11,2	13	14,8	16,6
mі	5	8	12	25	30	20	18	6

Определить: а) выборочную среднюю; б) выборочную дисперсию;в) выборочное среднее квадратическое отклонение.

Для решения задачи введём условную переменную

, где С – одно из значений х_і , как правило, соответствующее наибольшему значению m_і , а h– это шаг (у нас h = 1,8).

Пусть С = 11,2. Тогда .

Заполним таблицу:

xi	mi	xi ´	xi mi	(xi ´)²mi
4	5	– 4	– 20	80
5,8	8	– 3	– 24	72
7,6	12	– 2	– 24	48
9,4	25	– 1	– 25	25
11,2	30	0	0	0
13	20	1	20	20
14,8	18	2	36	72
16,6	6	3	18	54
∑ = 124	∑ = – 19	∑ = 371

Используя таблицу, найдём ;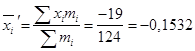

D(x´) = ∑(x_i ´)²m_i – (x_i ´)² = – (– 0,1532)² = 2,9685.

Теперь перейдем к фактическим значениям х и D(x):

_

x = x´h + C = – 0,1532∙1,8 + 11,2 = 10,9242;D(x) =D(x´)∙h² = 2,9685∙1,8² = 9,6178;

σ(x) = √D(x) = √9,6178 = 3,1013.

№ 61

По данной корреляционной таблиценайти выборочное уравнение регрессии.

у х	6	9	12	15	18	21	ny
5	4	2	6
15	5	23	28
25	18	44	5	67
35	1	8	4	13
45	4	2	6
nx	4	7	42	52	13	2	n= 120

Для упрощения расчетов введем условные переменные

u = , v = .Составим таблицу:

vu	– 3	– 2	– 1	0	1	2	nv	nuv uv
– 2	4 6	2 4	6	32
– 1	5 2	23 1	28	33
0	18 0	44 0	5 0	67	0
1	1–1	8 0	4 1	13	3
2	4 2	2 4	6	16
nu	4	7	42	52	13	2	n = 120	∑ = 84

Последовательно получаем:

;

;

;

;

σ_u ² = – (u)² = 1,058 – (– 0,425)² = 0,878; σ_u = √0,878= 0,937;

σ_v ² = – (v)² = 0,742 – (– 0,125)² = 0,726; σ_v = √0,726 = 0,8521;

По таблице, приведённой выше, получаем ∑n_uv uv = 84.

Находим выборочный коэффициент корреляции:

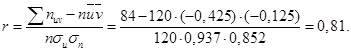
Далее последовательно находим:

x= u∙h₁ + C₁ = – 0,425∙3 + 15 = 13,725; y = v∙h₂ + C₂ = – 0,125∙10 + 25 = 23,75;

σ_x = σ_u ∙h₁ = 0,937∙3 = 2,811; σ_y = σ_v ∙h₂ = 0,8521∙10 = 8,521.

Уравнение регрессии в общем виде: 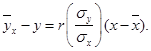Таким образом,

упрощая, окончательно получим искомое уравнение регрессии:

Необходимо произвести проверку полученного уравнения регрессии при, по крайней мере, двух значениях х.

1) при х = 12 по таблице имеем

по уравнению:

у_х=12 = 2,457∙12 – 9,968 = 19,516; ε₁ = 19,762 – 19,516 = 0,246;

2) при х = 18 по таблице имеем

по уравнению:

у_х=18 = 2,457∙18 – 9,968 = 34,258; ε₂ = 34,258 – 34,231 = 0,027.

Отмечаем хорошее совпадение эмпирических и теоретических данных.

Вариант 2

№ 2

Для сигнализации об аварии установлены 3 независимо работающие устройства. Вероятности их срабатывания равны соответственно р₁ = 0,9, р₂ = 0,95, р₃ = 0,85. Найти вероятности срабатывания при аварии:

а) только одного устройства;

б только двух устройств;

в) всех трёх устройств.

Обозначим события: А – срабатывает только одно устройство; В – срабатывают 2 устройства; С – срабатывают все 3 устройства. Вероятности противоположных событий (не срабатывания) соответственно равны q₁ = 0,1, q₂ = 0,05, q₃ = 0,15. Тогда

а) Р(А) = p₁ q₂ q₃ + q₁ p₂ q₃ + q₁ q₂ p₃ = 0,9∙0,05 ∙0,15 + 0,1∙0,95∙0,15 + 0,1∙0,05∙0,85 = 0,02525.

б) Р(В) = p₁ p₂ q₃ + p₁ q₂ p₃ + q₁ p₂ p₃ = 0,9∙0,95∙0,15 + 0,9∙0,05∙0,85 + 0,1∙0,95∙0,85 = 0,24725.

в) Р(С) = р₁ р₂ р₃ = 0,9∙0,95∙0,85 = 0,72675.

№ 12

В партии из 1000 изделий имеется 10 дефектных. Найти вероятность того, что из взятых наудачу из этой партии 50 изделий ровно 3 окажутся дефектными.

По условию n = 50, k = 3. Поскольку р малó, n достаточно большое, в то же время nр = 0,5 < 9, справедлива формула Пуассона:.

Таким образом,

№ 22

По данному закону распределения дискретной случайной величины Х определить математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение σ(Х).

хі	2	3	4	5	8
рі	0,25	0,15	0,27	0,08	0,25

Последовательно получаем:

5

М(Х) = ∑ х_і р_і = 2∙0,25 + 3∙0,15 + 4∙0,27 + 5∙0,08 + 8∙0,25 = 4,43.

i=1

5

D(X) = ∑ x_i ²p_i – M² = 2²∙0,25 + 3²∙0,15 + 4²∙0,27 +5²∙0,08 + 8²∙0,25 – 4,43² і=1

= 5,0451.

σ(Х) = √D(X) = √5,0451= 2,246.

№ 32

Случайная величина Х задана интегральной функцией

а) дифференциальную функцию f(x) (плотность вероятности);

б) математическое ожидание и дисперсию величины х;

в) вероятность того, что X примет значение, принадлежащее интервалу

;

г) построить графики функций F(x) и f(x).

Последовательно получаем:

а) ;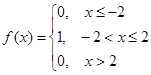

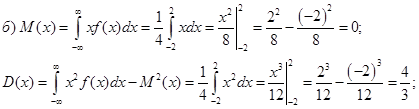
в) Р(a < x < b) = F(b) – F(a) ÞP= F(1) – F=

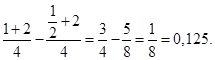
Графики функций приводятся далее.

№ 42

Определить вероятность того, что нормально распределённая величина Х примет значение, принадлежащее интервалу (α;β) если известны математическое ожидание а и среднее квадратическое отклонение σ. Данные: α = 5; β = 14; а = 9; σ = 5.

Используя формулу имеем

Поскольку функция Лапласа есть нечетная, можем записать:

№ 52

По данному статистическому распределению выборки

хі	7,6	8	8,4	8,8	9,2	9,6	10	10,4
mі	6	8	16	50	30	15	7	5

Определить: а) выборочную среднюю; б) выборочную дисперсию;в) выборочное среднее квадратическое отклонение.

Для решения задачи введём условную переменную

где С – одно из значений х_і , как правило, соответствующее наибольшему значению m_і , а h – это шаг (у нас h = 0,4).

Пусть С = 8,8. Тогда

Заполним таблицу:

xi	mi	xi ´	xi mi	(xi ´)²mi
7,6	6	– 3	– 18	54
8	8	– 2	– 16	32
8,4	16	– 1	– 16	16
8,8	50	0	0	0
9,2	30	1	30	30
9,6	15	2	30	60
10	7	3	21	63
10,4	5	4	20	80
∑ = 137	∑ = 51	∑ = 335

Используя таблицу, найдём

;

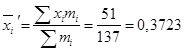D(x´) = ∑(x_i ´)²m_i – (x_i ´)² = – 0,3723² = 2,3067.

Теперь перейдем к фактическим значениям х и D(x):

x = x´h + C = 0,3723∙0,4 + 8,8 = 8,9489; D(x) = D(x´)∙h² = 2,3067∙0,4² = 0,3961;

σ(x) = √D(x) = √0,3961 = 0,6075.

№ 62

По данной корреляционной таблице

у х	4	8	12	16	20	24	ny
10	2	5	7
20	6	8	4	18
30	8	46	10	64
40	5	20	4	29
50	3	14	2	5	22
nx	2	19	62	48	6	3	n = 140

найти выборочное уравнение регрессии.

Для упрощения расчетов введём условные переменные

Составим таблицу.

vu	– 2	– 1	0	1	2	3	nv	nuv uv
– 2	2 4	5 2	7	18
– 1	6 1	8 0	4 –1	18	2
0	8 0	46 0	10 0	64	0
1	5 0	20 1	4 2	29	28
2	3 0	14 2	2 4	5 6	22	66
nu	2	19	62	48	6	3	n = 140	∑ = 114

Последовательно получаем:

;

;

;

;

σ_u ² = – (u)² = 0,9 – 0,329² = 0,792; σ_u = √0,792 = 0,89;

σ_v ² = – (v)² = 1,164 – 0,293² = 1,079; σ_v = √1,079 = 1,0385;

По таблице, приведённой выше, получаем ∑n_uv uv = 114.

Находим выборочный коэффициент корреляции:

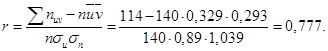
Далее последовательно находим:

x = u∙h₁ + C₁ = 0,329∙4 + 12 = 13,314; y = v∙h₂ + C₂ =0,293∙10 + 30 = 32,929;

σ_x = σ_u ∙h₁ = 0,89∙4 = 3,56; σ_y = σ_v ∙h₂ = 1,0385∙10 = 10,385.

Уравнение регрессии в общем виде: 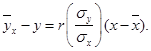Таким образом,

упрощая, окончательно получим искомое уравнение регрессии:

Необходимо произвести проверку полученного уравнения регрессии при, по крайней мере, двух значениях х.

1) при х = 12 по таблице имеем

по уравнению: у_х=12 = 2,266∙12 + 2,752 = 29,944; ε₁ = 30,484 – 29,944 = 0,54;

2) при х = 16 по таблице имеем

по уравнению: у_х=16 = 2,266∙16 + 2,752 = 39,008; ε₂ = 39,167 – 39,008 = 0,159.

Отмечаем хорошее совпадение эмпирических и теоретических данных.