Название: Симплекс-метод
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 60.45 Kb
Скачать файл: referat.me-217642.docx
Краткое описание работы: Материал инструмента и заготовки, вертикально-сверлильный станок. Ограничения по стойкости, мощности привода станка, кинематике и стойкости. Расчет целевой функции производительности, оптимальной точки режима резания. Оптимальное решение симплекс-методом.
Симплекс-метод
Тольяттинский Государственный Университет
Задачи по Математическому моделированию
Студент: Шелудяков И.В.
Группа: М-402
Преподаватель: Бобровский А.В.
Тольятти 2006г.
Материал инструмента: Р6М5
Материал заготовки: Чугун СЧ 21-40
Станок: Вертикально-сверлильный 2Н125
Nшп =45…2000 об/мин
S=0,1-1,6 мм/об
Nэд = 2,2 кВт
25мм
t=1,5мм
Инструмент: зенкер насадной со вставными ножами из быстрорежущей стали ГОСТ 2255-71
d=22-40 мм
L=60-100 мм
D=50-100 мм
Ограничения по:
Стойкости
Мощности привода станка
Кинематике
Ограничение по стойкости
, 
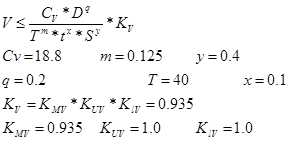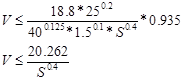
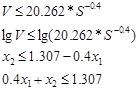
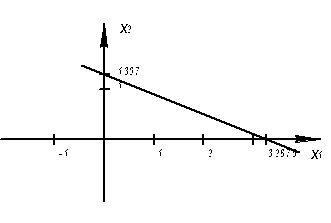
Ограничение по мощности привода
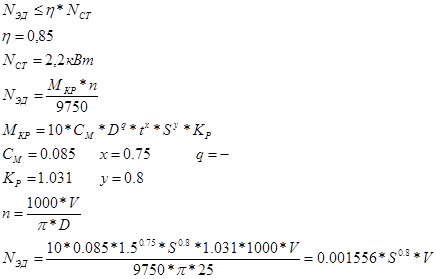
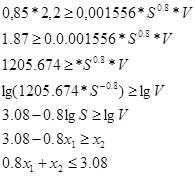
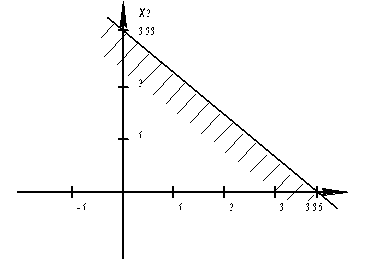
Ограничение по кинематике станка
Sоб min ≤ S ≤ Sоб max, Sоб min ≤ S, Sоб max ≥ S
lgSоб min ≤ lgSlg 0.1 ≤ x1 x1 ≥ - 1
lgSоб max ≥ lgSlg1.6 ≥ x1 x1 ≤ 0.204
lg3.534 ≤ x2
x2
≥ 0.5483
lg157.079 ≥ x2
x2
≤ 2.196
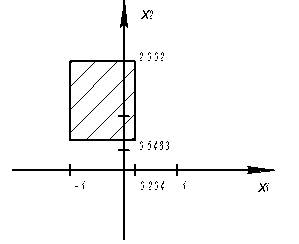
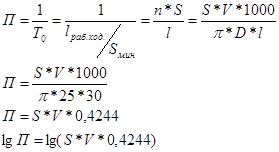
Целевая функция производительности
- функция производительности.
Если z = 1 , то x1 + x2 = 1.3722
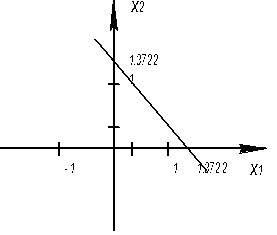
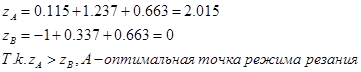
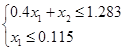
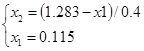
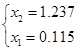
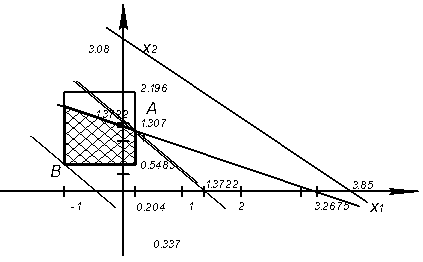
Симплекс – метод
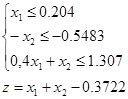
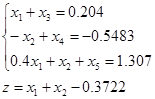
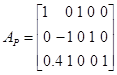
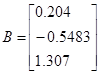
Выбираем базис и находим его решение:
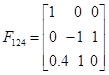
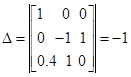
Найдем алгебраические дополнения для каждого элемента матрицы
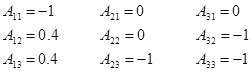
Союзная матрица Транспонированная матрица Обратная матрица
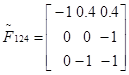
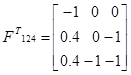
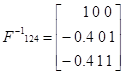
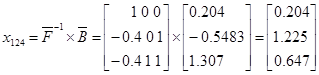
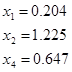
Базис 124 является допустимым т.к. все значения положительные.
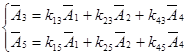
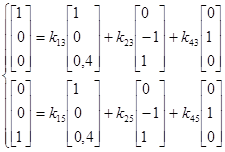
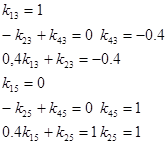
Найдем симплекс-разности.
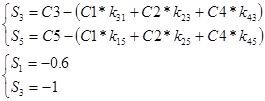
Решение является оптимальным.
Значения 
совпадают со значениями, полученными при решении задачи графическим способом.
Симплекс-таблицы.
, 
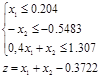
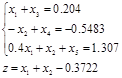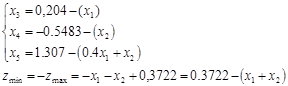
Табл. 1
СН БН |
СЧ | x1 | x5 |
| x3 | 0.204 | 1 | 0 |
| x4 | 0.7587 | 0.4 | 1 |
| x2 | 1.307 | 0.4 |   1 |
| zmin | 0.9348 | 0.6 | -1 |
Табл.2
| СЧ | x1
|
x2 | |
| x3 | 0.204 | 1 |  0 |
| x4 | -0.5483 | 0 | -1 |
| x5 | 1.307 | 0.4 | 1 |
| zmin | 0.3722 |  1 |
1 |
Табл.3
СН БН |
СЧ | x3 | x5 |
| x1 | 0.204 | 1 | 0 |
| x4 | 0.6771 | -0.4 | 1 |
| x2 | 1.2254 | -0.4 | 1 |
| zmin | 0.8124 | -0.6 | -1 |
В табл.3 все элементы последней строки отрицательные - min найден.
Значения
совпадают со значениями, полученными при решении задачи графическим способом и симплекс методом.
Похожие работы
-
Симплекс метод 2
Симплекс-метод Симплекс-метод Текущая версия (не проверялась) Не путать с «симплекс-методом» — методом оптимизации произвольной функции. См. Метод Нелдера — Мида
-
Типовой расчет по ЭМММ
Типовой расчет Решение задач по дисциплине ЭМММ Вариант №23 Выполнил: Проверил: Екатеринбург 2009 Математическая модель ЗЛП Мат. модель ЗЛП называется стандартной, если система ограничений представлена в виде неравенств, а функция минимизируется или максимизируется
-
Задача по Экономико-математическое моделирование
ФЕДЕРАЛЬНОЕ Вариант № . Нефтеперерабатывающий завод производит в месяц 1500000 л алкилата, 1200000 л крекинг - бензина и 1300000 л изопентола. В результате смешения этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сорта А и Б соответственно. Стоимость 1000 л бензина сорта А и Б соответственно равна 90 и 120 усл. ед..
-
Решение и постоптимальный анализ задачи линейного программирования
Теоретические положения симплекс-метода и постоптимального анализа. Построение математической модели задачи. Нахождение ценностей ресурсов. Определение относительных и абсолютных диапазонов изменения уровней запасов дефицитных и недефицитных ресурсов.
-
Решение задач линейного программирования
Министерство общего и профессионального образования Российской Федерации Воронежский Государственный Архитектурно – Строительный Университет
-
Задачи по Математике 3
Задача 1 Решить графическим методом задачу линейного программирования А) найти область допустимых значений многоугольник решений Б) найти оптимумы целевой функции
-
Оптимизация организационных решений
КОНТРОЛЬНАЯ РАБОТА по дисциплине « ОПТИМИЗАЦИЯ ОРГАНИЗАЦИОННЫХ РЕШЕНИЙ» Задание №1 Решение задачи об оптимальном направлении капиталовложений в строительную отрасль и оптимизации поставки строительных грузов
-
Исследование математических операций
Министерство образования и науки Украины Днепропетровский Национальный Университет Факультет электроники, телекоммуникаций и компьютерных систем
-
Математический расчет объема выпуска продукции
Задача №11 N=25 Завод выпускает изделия трех моделей (1, 2 и 3). Для изготовления используются 2 вида ресурсов А и В, запасы которых составляют 400 и 600 единиц. Расход ресурсов на одно изделие каждой модели приведен в таблице:
-
Записать задачу двойственную к данной, решить одну из пары задач и отыскать оптимальное решение второй
Графическое решение задачи линейного программирования. Общая постановка и решение двойственной задачи (как вспомогательной) М-методом, правила ее формирования из условий прямой задачи. Прямая задача в стандартной форме. Построение симплекс таблицы.