Название: Математическая логика и теория алгоритмов 2

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 120.36 Kb

Скачать файл: referat.me-217885.docx

Краткое описание работы: Томский межвузовский центр дистанционного образования Томский государственный университет систем управления и радиоэлектроники (ТУСУР) Контрольная работа № 1

Математическая логика и теория алгоритмов 2

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Контрольная работа № 1

по дисциплине

«Математическая логика и теория алгоритмов»

автор учебного пособия:

Зюзьков В.М.

Выполнил:

Студент ТМЦДО

специальности 220201

Вариант №11

1) Перевести на формальный язык (обязательно указывая универсум):

«Некоторые лентяи на оптимисты, но жизнелюбы».

Универсум М ={люди}. Предикаты: L(x) ≡ «х – лентяй», O(x) ≡ «х – оптимист», Z(x) ≡ «х – жизнелюб».

Формула:

2) Перевести на формальный язык (обязательно указывая универсум):

«Два философа сидят за столом и спорят»

Универсум М ={люди}. Предикаты: F(x) ≡ «х – философ», S(x) ≡ «х – сидит за столом», С(x,y) ≡ «х спорит с y»

Формула:

3) Перевести с формального языка на человеческий:

(R – Множество вещественных чисел).

Перевод: Для любого вещественного числа есть большее, синус которого равен нулю.

4) Перевести на формальный язык (обязательно указывая универсум):

«Ни один судья не справедлив».

Универсум М ={люди}. Предикаты: J(x) ≡ «х – судья», S(x) ≡ «х – справедлив».

Формула:

5) Является ли формула

тавтологией?

Использовать метод доказательства от противного.

Тавтология – формула, истинная независимо от того какие значения принимают переменные входящие в неё. Соответственно нам необходимо доказать, что она не может быть ложной. Представим, что формула ложна при некотором сочетании переменных.

(подставили в формулы значения q, r и t )
Желая избежать противоречия примем , получим
, противоречия нет.

Получили значения переменных, при которых формула является ложной, следовательно, она опровержима и не является тавтологией .

6) При каких значениях переменных формула

ложна?

Переберём все возможные комбинации.

1. Из утверждения получаем, что и одновременно невозможно.

2. Из утверждения получаем, что и одновременно невозможно

3. Из утверждения получаем, что и одновременно невозможно

4. Возьмём и , получаем (верно), (верно), (верно).

выполняется.

Ответ: формула ложна только при и , других вариантов нет.

7) Является ли формула

тавтологией?

(подставили в формулы значения Л, r и t )
Так как и , то подставим и получим
- противоречие.

Пришли к противоречию, следовательно, исходная формула – тавтология.

8) Проверить, что и

Решение: Сначала следует попробовать опровергнуть это утверждение, т.е. найти такие множества A, B и C , чтобы выполнялось отношение , но не выполнялось и или, наоборот, выполнялось и , но не выполнялось . После безуспешных попыток найти такие множества следует доказать данное утверждение.

Доказательство распадается на два этапа.

1. Докажем сначала, что и . Пусть и выполнено, докажем, что . Поскольку требуется доказать включение множеств, то возьмем произвольный элемент , следовательно (из ), значит и тем более . Аналогично для .

2. Докажем теперь, что и . Пусть выполнено, докажем, что и . Поскольку требуется доказать включение множеств, то возьмем произвольный элемент , однозначно . Значит и тогда . Аналогично для B . Доказательство закончено.

9) Проверить, что

Это выражение верно, так как согласно не существует элемента , который не входил бы в . Следовательно, для , . Обратное не верно.

10) Проверить тождество

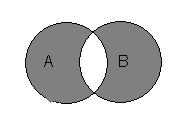
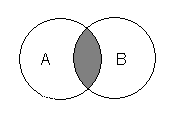
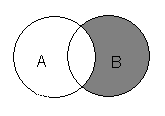
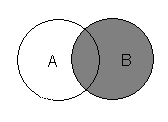
Решение. Построим диаграмму Эйлера для левого множества в четыре этапа.

Диаграмма для множества	Диаграмма для множества

Диаграмма для множества	Диаграмма для множества

Диаграммы Эйлера показывают, что тождество выполняется. Докажем это. Используя основные тождества алгебры множеств, преобразуем левую и правую части к одному множеству.

Преобразуем отдельно первое и второе множества.