Название: Изучение и анализ различных способов определение тригонометрических функций

Вид работы: курсовая работа

Рубрика: Математика

Размер файла: 497.37 Kb

Скачать файл: referat.me-217946.docx

Краткое описание работы: МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Изучение и анализ различных способов определение тригонометрических функций

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики и компьютерных наук

Кафедра математики и информатики

Курсовая работа

«Изучение и анализ различных способов определение тригонометрических функций»

Выполнил:

студентка 362 группы

Латфуллина Р.А.

Научный руководитель:

к.ф.-м.н., доцент

Шармина Т.Н.

Тюмень - 2010

Содержание

Введение. 3

Глава1. Функции , как решения некоторых задач Коши. 5

Глава2. Аналитическая теория тригонометрических функций. 16

Список литературы.. 22

Введение

Данная курсовая работа посвящена изучению и анализу различных способов определения тригонометрических функций.

Тригонометрические функции являются важной составной частью содержания математического образования, как в средних, так и в высших учебных заведениях и часто встречаются в различных приложениях математики. С их помощью могут быть построены и изучены математические модели процессов реального мира. Для школьных учителей полезно знать различные подходы к определению и изучению свойств тригонометрических функций. Имеется не так много математической литературы в которой теория элементарных функций излагается последовательно и подробно разными методами. В этом и заключается актуальность данной темы.

Объектом нашего исследования мы выбрали тригонометрические функции. Предметом же является способы их определения.

Целью курсовой работы является изучение и анализ различных способов определения тригонометрических функций.

Для достижения цели мы поставили следующие задачи: изучить математическую литературу, проанализировать способы определения тригонометрических функций и доказать свойства этих функций на основе соответствующего способа определения.

Курсовая работа состоит из введения, двух глав и списка литературы.

В главе 1 излагается способ построения теории функций , , основываясь на использовании теоремы существования и единственности решения соответствующей задачи Коши и простейших сведений из дифференциального и интегрального исчисления. Также в этой главе приведены доказательства основных свойств этих функций.

Глава 2 посвящена рассмотрению теории тригонометрических функций на базе степенных рядов и установлению эквивалентности нового и традиционного определения таких функций.

Также в работе проведены доказательства некоторых свойств тригонометрических функций.

Глава1. Функции , как решения некоторых задач Коши

Для линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами теорема существования и единственности решения задачи Коши формулируется следующим образом.

Теорема1 . Дифференциальное уравнение

,

где ; ; ; , имеет на единственное n-кратно дифференцируемое решение , удовлетворяющее условиям

(здесь - произвольно заданные фиксированные действительные числа).

Очевидно, что это решение обладает на непрерывными производными всех порядков.

В частности, когда , указанное в теореме 1 решение тривиально ( на ).

Рассмотрим следующие две задачи Коши:

, , ; (1)

, , , (2)

где ; ; . Их решения обозначим соответственно через и . Согласно теореме 1, эти решения определены, непрерывны и бесконечно дифференцируемы на всей числовой прямой, причём , . Однако основные свойства функций , установим, исходя из определения их как решения задач (1) и(2).

1. , ().

Действительно, так как и - решения уравнения , то , , откуда , . Это значит, что каждая из функций , также являются решением уравнения . При этом решения и удовлетворяют одним и тем же начальным условиям: , . Следовательно, по теореме существования и единственности на , т.е. для .

Аналогично убеждаемся и в справедливости соотношения

().

2. Функция нечётная, а чётная.

Доказательство: Прежде всего, области определения этих функций (совпадающие с ) симметричны относительно точки . Покажем теперь, что и при любом .

Вводя в рассмотрение функции и (тогда , ) и учитывая свойство 1, будем иметь:

,

, ;

,

.

Таким образом, функции и являются решением одной и той же задачи Коши , , . Поэтому (согласно теореме 1) на , т.е. для любого .

Подобным же образом убеждаемся, что функция является решением задачи Коши , , , следовательно, на .

3. Имеет место тождество .

Доказательство. Полагая и используя свойство 1, находим

(),

Вследствие чего на . А так как , то на , т.е. на .

Замечание. Из свойства 3 следует, что функции и ограничены , причём , для любого .

4. Справедливы следующие соотношения (теоремы сложения для функций и ):

() (3) Доказательство. Введём в рассмотрение функции

Считая (без ограничения общности) постоянной, а переменной. Эти функции являются решениями уравнения , удовлетворяющими нулевым условиям. Действительно, так как , :

так что

(на ),

Аналогично

(на ), , .

Следовательно, согласно теореме 1, и на . Из этих тождеств непосредственно следуют требуемые соотношения.

Замечание. Пологая в формулах (3) , получаем следующие формулы удвоения :

, ().

Отсюда с учётом свойства 3 получаем:

, ().

Изучим теперь вопрос о нулях функций , , т.е. о корнях уравнений , . Для краткости в дальнейшем нуль функции, принадлежащий , будем называть её положительным нулём .

Так как , то число является одним из нулей функции .

Лемма1 . Хотя бы одна из функций , обладает по крайней мере одним положительным нулём.

Доказательство . Предположим (от противного), что уравнения , положительных решений не имеют. Тогда на функции и знакопостоянны. Действительно, если бы функция или в некоторых точках принимала значения противоположных знаков, то по теореме Больцано-Коши нашлась бы точка, заключённая между и , в которой эта функция обращалась бы в нуль вопреки допущению.

Учитывая, далее, что , заключаем, вследствие непрерывности , что положительна в некоторой окрестности точки , и, следовательно, на .

Функция возрастает на , так как на , а поскольку , то на . С учётом свойства 3 и положительности функций , на имеем

т.е. для любого . Очевидно, сто последнее неравенство верно и при . Интегрируя почленно это неравенство по промежутку , где - любое положительное число, большее двух, получаем

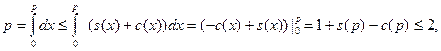
т.е. вопреки выбору числа . Полученное противоречие и доказывает лемму.

Лемма2 . Функция имеет хотя бы один положительный нуль.

Доказательство. Допустив противоречие, получим, что согласно лемме1, функция обладает хотя бы одним положительным нулём , а тогда (по формуле удвоения для функции ) будем иметь

,

т.е. - положительный нуль функции , но это противоречит допущению.

Замечание . Если , то и для любого .

Доказательство. Для , -это известно.

Пусть для утверждение верно, т.е. . Докажем справедливость утверждения для .

Используя свойство 4, вычислим :

т.к. и .

5. Существует наименьший положительный нуль функции .

Доказательство. Обозначим через множество положительных нулей функции . Это множество бесконечно (на основании леммы 2 и замечания к ней) и ограничено снизу (например, числом 0). Пусть . Очевидно, что . Предположим теперь, что функция не обладает наименьшим положительным нулём. С учётом этого предположения и определения точной нижней грани множества получаем, что - предельная точка множества . Теперь легко убедиться, что является одним из нулей функции . Действительно,

(здесь мы воспользовались непрерывностью функции и теоремой о пределе функции (в нашем случае ) в точке по данному множеству , для которого является предельной точкой). Отсюда следует, что (поскольку в случае число было бы наименьшим положительным нулём функции вопреки сделанному выше предположению).

Но при имеем

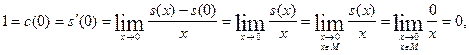
т.е. . Поскольку полученное равенство ложно, то наше допущение об отсутствии наименьшего положительного нуля функции неверно, и тем самым требуемое свойство доказано.

Обозначим наименьший положительный нуль функции через . Выясним свойства функций и , прямо или косвенно связанные с числом ().

6. Функция положительна на интервале и отрицательна на интервале .

7. Функция убывает на и возрастает на .

8. Числа вида и только эти числа являются нулями функции .

Доказательство. Согласно замечанию к лемме 2, (). Если же (), то . Для доказательства этого допустим противное, т.е. предположим, что существует число (), такое что . Без ограничения общности (учитывая нечётность функции ) можем считать, что . Пусть . Положим . Очевидно, что . Кроме того, на основании свойств 2 и 4 получим

т.е. функция имеет нуль в интервале вопреки определению числа .

9. , ; , .

10. Функция положительна на и отрицательна на .

Доказательство.

1) Докажем, что на .

, (по свойству 9). Найдём :

, т.к. , то , следовательно , т.е . Учитывая свойство 7 получим, что - наименьший положительный нуль функции .

Учитывая, что и свойство 7, получаем, что - наибольший отрицательный нуль функции .

Таким образом, но интервале функция не имеет нулей. По теореме Больцано-Коши функция будет знакопостоянной на этом интервале. Кроме того, функция положительна в некоторой правосторонней окрестности точки (в силу того, что (по свойству 9) ). Следовательно, на всём интервале , следовательно, и на .

2) Докажем, что на .

(по свойству 9). Найдём :

, т.к. , то , следовательно , т.е . Учитывая свойство 7 получим, что - наибольший отрицательный нуль функции .

Таким образом, но интервале функция не имеет нулей. По теореме Больцано-Коши функция будет знакопостоянной на этом интервале. Кроме того, функция отрицательна в некоторой правосторонней окрестности точки (в силу того, что , ). Следовательно, на всём интервале .

11. .

Действительно, из равенства имеем , откуда, учитывая, что , получим .

12. Функция возрастает на и убывает на .

Доказательство. Прежде всего, функция непрерывна на каждом из отрезков и и дифференцируема на .

Так как , то учитывая свойство 10, на и на .Требуемое утверждение теперь непосредственно следует из теоремы о достаточных условиях убывания (возрастания) функции на промежутке.

Замечание . Из свойства 2 и 12 следует, что функция убывает на и возрастает на .

13. Функции ,- периодические с периодом .

Доказательство. Применяя теоремы сложения и учитывая, что , , имеем при любом :

,

,

т.е. - период функций ,.

Докажем теперь, что ни одна из функций , не имеет положительного периода, меньше . Действительно, наличие такого периода у функции противоречит свойству 7, а если бы таким периодом обладала функция , то мы имели бы , т.е. , откуда . Поэтому , т.е. , что невозможно.

14. Нулями функции являются числа вида и только эти числа.

Действительно, согласно тождеству , нулями функции все те и только те числа , для которых . Последнее же уравнение на отрезке (длина которого равна периоду функции ) имеет два решения: и (на основании свойств 2,9,12 и замечания к свойству 12). Для завершения доказательства остаётся воспользоваться свойством 13 и заметить, что полученные две серии решений

,

уравнения можно объединить в одну:

.

15. Справедливы следующие тождества (формулы приведения ):

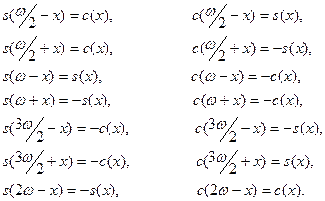
Доказательство. Убедимся, например, что .

Учитывая свойства 4, 2, замечание к лемме 2 и свойство 3, имеем

.

Аналогично убеждаемся в справедливости остальных тождеств.

16. Наименьший положительный нуль функции равен .

Доказательство. Рассмотрим на координатной плоскости круг . Его площадь, как известно, равна . С другой стороны, эта площадь равна , где -площадь четверти данного круга, расположенной в первом квадранте. Так как

,

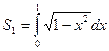то

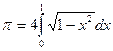
Вводя подстановку и учитывая, что при возрастании от до функция (т.е. ) возрастает от до , получаем

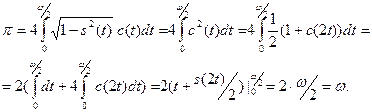
Итак, .

Глава2. Аналитическая теория тригонометрических функций

Функции действительной переменной, представимые в некотором интервале из степенными рядами, называются аналитическими в этом интервале.

Тригонометрические функции являются аналитическими, т.е. могут быть представлены степенными рядам.

Рассмотрим степенные ряды

(1)

(2)

Эти ряды сходятся, и притом абсолютно, при любом действительном , в чём легко убедиться по признаку Д’Аламбера. Действительно, при любом

,

.

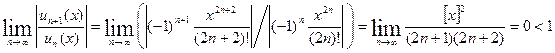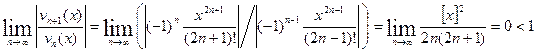Следовательно, функции и как суммы соответствующих степенных рядов (1) и (2) определены и непрерывны на интервале . Более того, эти функции дифференцируемы на , причём

Функция чётная, а нечётная, так как , для любого .

Установим ещё некоторые свойства функций и .

Теорема1. Для любого действительного

. (3)

Доказательство. Имеем

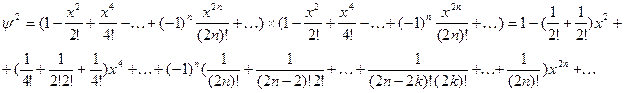
Коэффициент при можно представить в виде

ибо - число сочетаний из элементов по

Аналогично

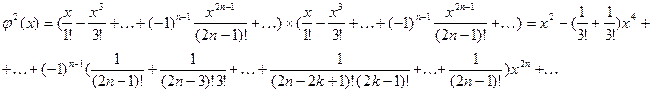
Коэффициент при можно представить в виде

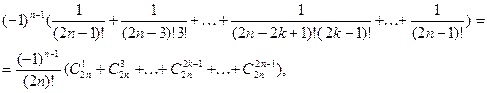
ибо

При сложении и коэффициент при будет равен

Выражение в скобках равно нулю, в чём можно убедиться, полагая , в формуле бинома Ньютона

Таким образом, .

Следствие. Функции и ограниченные, причём и

Теорема 2 . (теорема сложения для функций и ). Для любых действительных и

(4)

(5)

Доказательство . Проверим формулу:

Имеем:

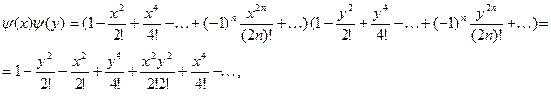
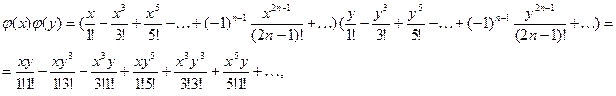
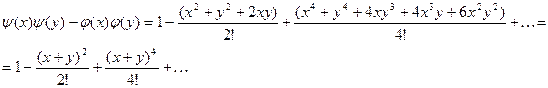
Рассмотрим общий член этого ряда, содержащий произведения вида: , где . Получим

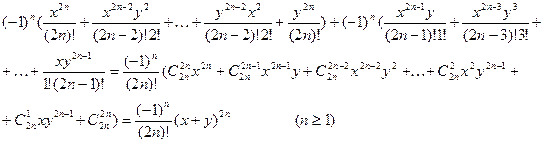
ибо

Таким образом,

.

Используя чётность или нечётность функций и , проверим справедливость формулы:

Имеем

Аналогично проверяется справедливость формул

Теорема3. Для любых действительных и функция удовлетворяет уравнению

(6)

Доказательство. По определению функцииимеем:

Вычислим - общий член ряда для суммы

Далее,

Вычислим - общий член ряда для произведения

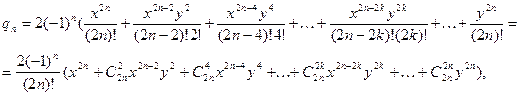
ибо Получим, что при , а поскольку , то при любых действительных и имеет место равенство (6).

Замечание1. Из формул сложения (3) и (4) следуют формулы двойного аргумента:

(7)

Замечание2. Непосредственно из формул (3) и (7) получим:

Теорема4. Ф ункция имеет по крайней мере один положительный нуль.

Доказательство. Так как для любого

то

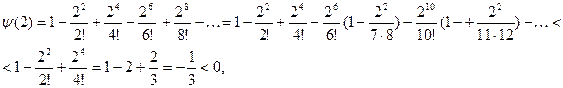
и по теореме о промежуточных значениях непрерывной на отрезке функции на имеет по крайней мере один нуль, т.е. существует число , такое, что .

Теперь справедливы следующие утверждения.

1. Функция имеет наименьший положительный нуль , иными словами, существует , такое, что .

2. Имеют место равенства:

3. Функция положительна на интервале , а функция - на интервале .

4. Функция возрастает на отрезке .

5. Функция убывает на отрезке и возрастает на отрезке .

6. .

7. Нулями функции являются числа и только такие числа, а функции - числа

8. Функции и являются периодическими с наименьшим положительным периодом .

9. Имеют место формулы приведения:

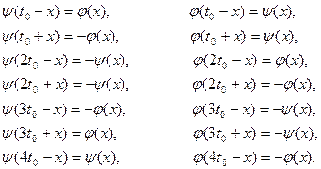
10. Наименьший положительный нуль функции равен .

Список литературы

1. Архипов Б.М., Мазаник А.А., Петровский Г.Н., Урбанович М.И., Элементарные функции: Учеб. Пособие.- Мн.: Выш. шк., 1991.-140с.2. Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления: том I-Спб.: Издательство «Лань», 1997.-800с.