Название: Фундаментальная группа. Конечные поля

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 303.59 Kb

Скачать файл: referat.me-218140.docx

Краткое описание работы: Конечные поля Цель работы: Изучить конструкцию и простейшие свойства конечных полей. В частности, изучить на примерах конечных полей понятие степени расширения, конструкцию и однозначную определенность поля разложения, простые поля, понятие примитивного элемента, строение конечной, мультипликативной подгруппы поля.

Фундаментальная группа. Конечные поля

Конечные поля

Цель работы: Изучить конструкцию и простейшие свойства конечных полей. В частности, изучить на примерах конечных полей понятие степени расширения, конструкцию и однозначную определенность поля разложения, простые поля, понятие примитивного элемента, строение конечной, мультипликативной подгруппы поля. Познакомиться с арифметикой конечных полей. Решить упражнение.

Докажем, что многочлен

неприводим над

.

.

Корней нет. => Многочлен неприводим.

Построим расширение поля степени . Пусть – корень , т.е.

,

тогда

Получим : .

расширение степени 3.

Разделим

.

.=

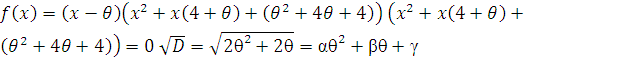Cоставим систему:

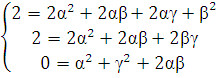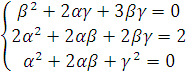=> Пусть , тогда =>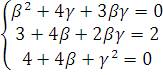

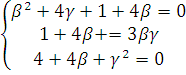
При β=3 => 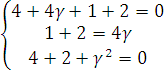γ=2

Отсюда получаем, что

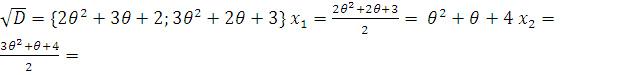
следовательно . Если q порождает – то, он примитивный. Найдем порядок . Так как порядок элемента делит порядок группы, порядок может быть 2, 4, 31, 62, 124.

.

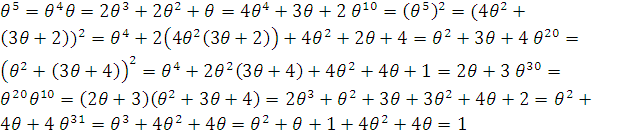
Элемент θ – не является примитивным элементом GF (125), т.к не выполняются условия. Программа, проверяющая, будет ли примитивным элементом поля .

TForm1 *Form1;

class Polynom

{ public:

int *coef;

int deg;

Polynom();

Polynom(char *);

Polynom(int);

Polynom(Polynom *);

~Polynom();

Polynom operator =(string);

Polynom *operator *(Polynom *);

Polynom operator /(Polynom);

Polynom *operator %(Polynom *);

int operator [](int);

void operator ++();

bool operator <(Polynom *);

bool operator ==(Polynom *);

Polynom *norm();

int coef_count();

char *print();

};

Polynom :: Polynom()

{ coef = new int[1];

coef[0] = 0;

deg = 0;

}

Polynom *Polynom :: norm()

{ int f = 0;

for(int i = 0; i <= deg; i++)

if( coef[i] != 0 )

{ f = i;

break;

}

int deg_tmp = deg - f;

Polynom *tmp = new Polynom(deg_tmp+1);

for(int i = f; i <= deg; i++)

tmp->coef[i-f] = coef[i];

return tmp;

}

Polynom :: Polynom(char *str)

{ deg = strlen(str)-1;

coef = new int[deg+1];

for(int i = 0; i <= deg; i++)

coef[i] = str[i] - 48;

}

Polynom :: Polynom(int d)

{ deg = d-1;

coef = new int[d];

for(int i = 0; i <= deg; i++)

coef[i] = 0;

}

Polynom :: Polynom(Polynom *p)

{ coef = p->coef;

deg = p->deg;

}

Polynom :: ~Polynom()

{ delete coef;

}

int Polynom :: operator[](int it)

{ return ( coef[it] );

}

int Polynom :: coef_count()

{ int count = 0;

for(int i = 0; i <= deg; i++)

{ if( coef[i] > 0 )

count++;

}

return count;

}

Polynom *Polynom :: operator*(Polynom *B)

{ Polynom *A = this;

Polynom *C = new Polynom(A->deg + B->deg + 1);

for(int i = A->deg; i >= 0; i--)

{ for(int j = B->deg; j >= 0; j--)

{ C->coef[i+j] += A->coef[i] * B->coef[j];

C->coef[i+j] %= 5;

}

}

return C;

}

bool Polynom :: operator <(Polynom *b)

{ if( deg < b->deg )

return true;

else

return false;

}

bool Polynom :: operator ==(Polynom *B)

{ Polynom *A = this;

if( A->deg != B->deg )

return false;

for(int i = 0; i <= A->deg; i++)

if( A->coef[i] != B->coef[i] )

return false;

return true;

}

int obr(int a)

{ a = 5 - a;

a %= 5;

return a;

}

Polynom *Polynom :: operator %(Polynom *B)

{ Polynom *tmp = this;

if( tmp->deg < B->deg )

{ return tmp;

}

for(int i = 0; i <= B->deg-tmp->deg; i++)

if(tmp->coef[i] >= 1)

{ int tmp_coef = tmp->coef[i];

tmp->coef[i] = 0;

for(int j = 1; j <= B->deg; j++)

{ tmp->coef[j] += obr(B->coef[j])*tmp_coef;

tmp->coef[j] %= 5;

}

}

tmp = tmp->norm();

return tmp;

}

void Polynom :: operator++()

{ bool flag = false;

for(int i = deg; i >= 0; i--)

{ coef[i]++;

coef[i] %= 5;

if( coef[i] == 0 )

{ flag = true;

}

else

flag = false;

if( flag == false )

break;

}

if( flag )

{ int *tmp = new int[deg+2];

tmp[0] = 1;

for(int i = 1; i <= deg+1; i++)

{ tmp[i] = coef[i-1];

}

coef = tmp;

deg = deg+1;

}

}

char *Polynom :: print()

{ char *s = new char[deg*3+(deg-1)*3 + deg*3 + deg*3];

int i = 0, f = 0;

s[0] = 0;

while ( i <= deg )

{ if (coef[i])

{ if(f)

strcat(s," + ");

f = 1;

switch(deg-i)

{ case 0:

wsprintfA(s, "%s%d", s, coef[i]);

break;

case 1:

if( coef[i] == 1 )

wsprintfA(s, "%sq", s);

else

wsprintfA(s, "%s%d*q", s, coef[i]);

break;

default:

if( coef[i] == 1)

wsprintfA(s, "%sq^%d", s, deg-i);

else

wsprintfA(s, "%s%d*q^%d", s, coef[i], deg-i);

};

}

i++;

}

if(!f)

strcat(s, "0");

return s;

}

bool TestPrimitive(Polynom *poly, Polynom *irr)

{ Polynom *tmp = poly;

Polynom *one = new Polynom("1");

for(int i = 2; i < pow((double)5, irr->deg); i++)

{ poly = (*poly) * tmp;

poly = (*poly) % irr;

Form1->Memo1->Text = Form1->Memo1->Text + "q^" + i + " =" + ' ';

Form1->Memo1->Text = Form1->Memo1->Text + poly->print();

Form1->Memo1->Lines->Add("");

if( *poly == one && i != pow((double)5, irr->deg)-1 )

{

Form1->Memo1->Text = Form1->Memo1->Text + i;

Form1->Memo1->Lines->Add("");

return false;

}

}

return true;

}

Polynom *DecToBin(int q)

{ string m = "";

int a;

do

{ if( q % 2 == 0 )

m += "0";

else

m += "1";

q /= 2;

} while( q != 0 );

Polynom *poly = new Polynom(m.size());

for(int i = 0; i < m.size(); i++)

poly->coef[i] = m[m.size()-i-1] + 48;

return poly;

}

Polynom *FindPrimitiveElement(Polynom *irr)

{ Polynom *test = new Polynom("4");

while( test->deg <= irr->deg )

{

(*test)++;

Form1->Memo1->Text = Form1->Memo1->Text + "q^" + 1 + " =" + ' ';

Form1->Memo1->Text = Form1->Memo1->Text + test->print();

Form1->Memo1->Lines->Add("");

if( TestPrimitive(test, irr) )

break;

}

return test;

}

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

{

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{ Polynom *IrrPoly = new Polynom(LabeledEdit1->Text.c_str()); // Считываем многочлен

Memo1->Text = Memo1->Text + "Неприводимый многочлен: " + IrrPoly->print(); // Вывожу

Memo1->Lines->Add("");

Polynom *prim = FindPrimitiveElement(IrrPoly); // Находимпримитивныйэлементполя

LabeledEdit2->Text = prim->print(); Результаты выполнения программы:

Фундаментальная группа

Цель работы: изучить определение и свойства фундаментальной группы топологического пространства. Познакомиться с понятием клеточного комплекса, со способом построения клеточного комплекса путем последовательного приклеивания клеток. Научиться задавать группы с помощью образующих и их соотношений (т. е. с помощью копредставлений) и распознавать группы по их копредставлениям. Научиться применять алгоритм вычисления фундаментальной группы клеточного комплекса.

Список групп-эталонов:

1. Циклические группы:

< x / = 1>, x – любое

2. Бинарные группы диэдра:

= < x, y / = = >, n ≥ 2

3. Бинарные группы тетраэдра и октаэдра:

= < x, y / = = , >, n = 1, 2

4. Группы вида:

= < x , y / >, k ≥ 2,

5. Прямые произведения вышеуказанных групп на циклические.

Во всех случаях индекс внизу показывает число элементов групп.

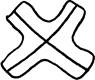На рисунке условно изображен двумерный клеточный комплекс, т.е. топологическое пространство, получающееся приклеиванием нескольких двумерных клеток (дисков) к одномерному комплексу (графу). Рисунок нужно понимать так: каждая «деталь» вида символизирует вершину графа, каждая склейка «отростков» вида

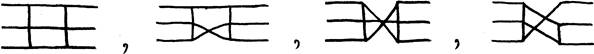
1. – ребро. Например, рисунок А символизирует граф на рисунке В.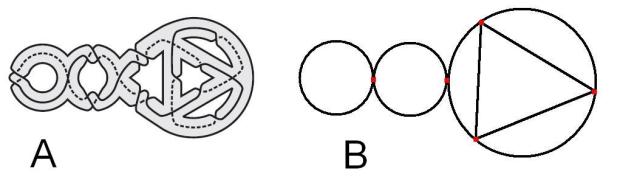

Далее требуется получить копредставление фундаментальной группы, для этого проделаем следующее:

1) По очереди разрезаем рёбра графа, обозначая их буквами и указывая направления до тех пор, пока не получится дерево (связанный граф без циклов), см. рис. ниже. Эти буквы будут служить образующими группы:

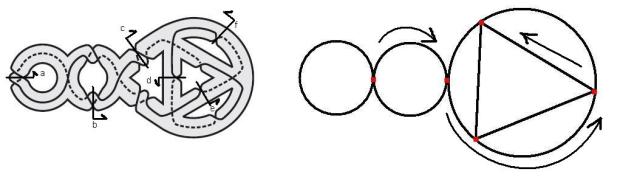
2) Выписываем соотношения (слова), которые показывают, как кривые проходят по разрезанным рёбрам. Эти соотношения таковы: 1. 2. =1 3. =1 4. =1 5. =1 6. =1 3)Приводим выписанное копредставление к копредставлению одной из эталонных групп.

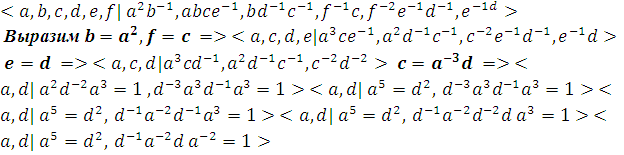Введём 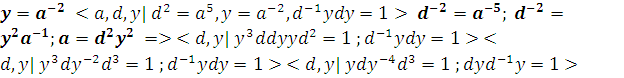В итоге получается , а именно