Название: Задача по Математике
Вид работы: реферат
Рубрика: Математика
Размер файла: 125.49 Kb
Скачать файл: referat.me-218172.docx
Краткое описание работы: Исследовать абсолютную устойчивость нелинейной системы: 1. Определить K = Kгр, при котором система находится на границе устойчивости: Параметры реле:
Задача по Математике
Исследовать абсолютную устойчивость нелинейной системы:
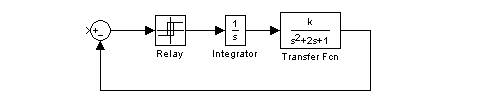
1. Определить K = Kгр, при котором система находится на границе устойчивости:
Параметры реле:
- включение x = 0.5;
- выключение x = - 0.5;
- на выходе при включении z(x) = 1;
- на выходе при выключении z(x) = -1;
z = f(x)
f(0) = 0
0 < f(x)/x < Kн
Kн = tgα = 1/0.5 =2
Нелинейная характеристика находится в 1 и 3 квадрантах, удовлетворяет выше перечисленным условиям =>
Допустимо использовать критерий В.М. Попова для исследования абсолютной устойчивости нелинейной системы.
Передаточная функция линейной части:
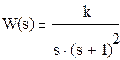
![]()
Q(s) = 0, βι < 0, полюсы левые => ЛЧ устойчива.
=>
Допустимо использовать критерий В.М. Попова для исследования абсолютной устойчивости нелинейной системы.
Передаточная функция линейной части:
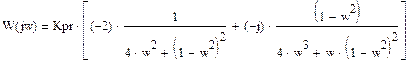
Преобразованная передаточная функция линейной части:
Wp(s) = Re(W(s)) + jwIm(W(s))
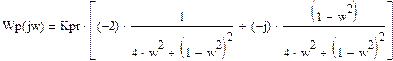
![]()
γ >0 – любое.
Строим годограф преобразованной ЛЧ ( в данном случае Kpr = 1.5)
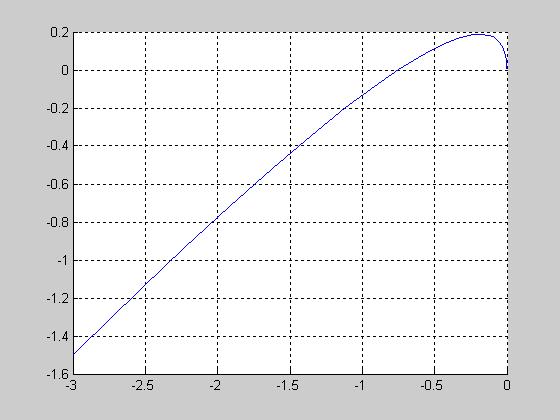
Находим точку пересечения годографа преобразованной ЛЧ с мнимой осью:
Im(Wp(jw)) = 0;
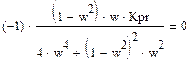
![]()
Re(W(jw))|{Im(W(jw))=0} = Kpr*(-0.5)
Kprвыбираем из условий: преобразованная частотная характеристика должна лежать справа от прямой, проведенной через точку -1/Kн на вещественной оси комплексной плоскости. Угол наклона ζ = arctg(1/τ).
(-0.5)Kpr > -1/Kн
=> Kpr < 1.
Вывод: при Kpr = 1 система находится на границе устойчивости.
2. Исследование автоколебаний (метод гарм. баланса):
Вычисляем передаточную функцию НЭ.
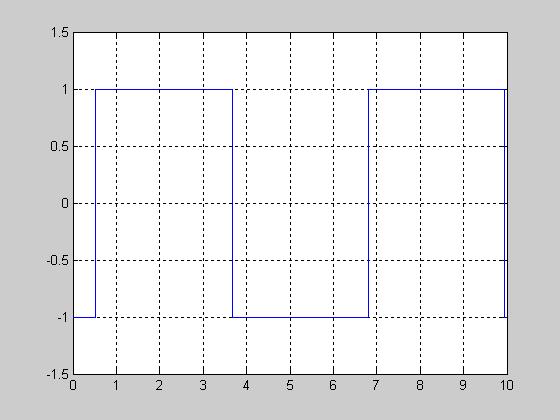
Wнэ(A) = q(A);
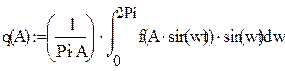
![]()
![]()
![]()
![]()
Колебания не возникнут, если отрицательный инверсный годограф НЭ не пересечет годограф ЛЧ ( Wлч = -1/q(A)).
Отрицательный инверсный годограф НЭ:
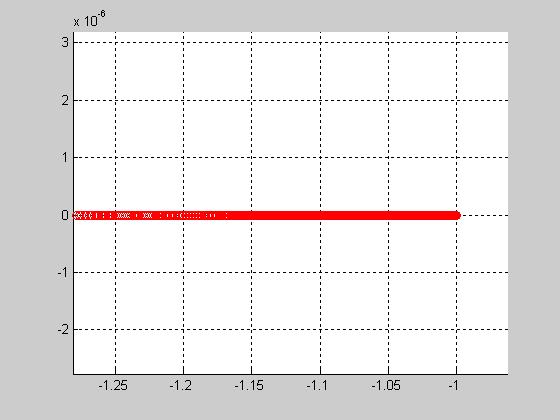
Отрицательный инверсный годограф НЭ и годограф ЛЧ :
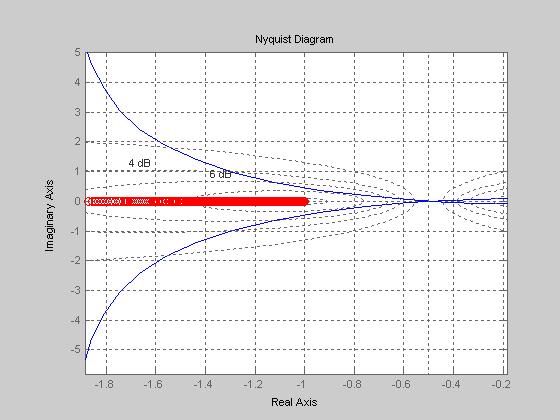
- Колебания не возникнут.
3. При K = 1.1Kprсинтезировать корректирующее устройство:
Строим годограф преобразованной ЛЧ ( в данном случае Kpr = 1.1)
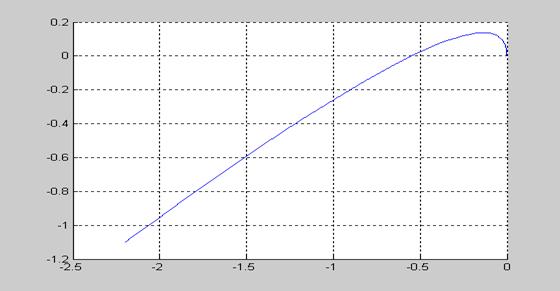
Для стабилизации системы вводим дополнительное звено Wф=(T1*p +1),
T1=1/w0, T1=1/0.9=1.1
Передаточная функция скорректированной системы:
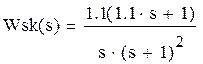
Строим годограф скорректированной преобразованной части:
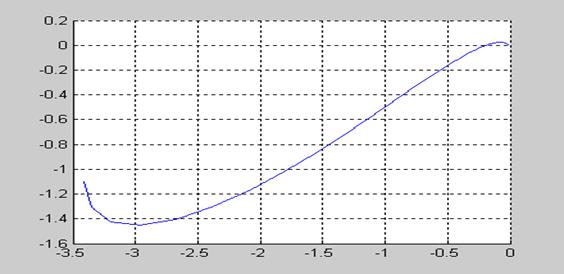
Через точку -1/Kн на вещественной оси комплексной плоскости можно провести прямую(угол наклона ζ = arctg(1/τ) ), так чтобы преобразованная скорректированная частотная характеристика лежала справа от прямой.
=> Система абсолютно устойчива.
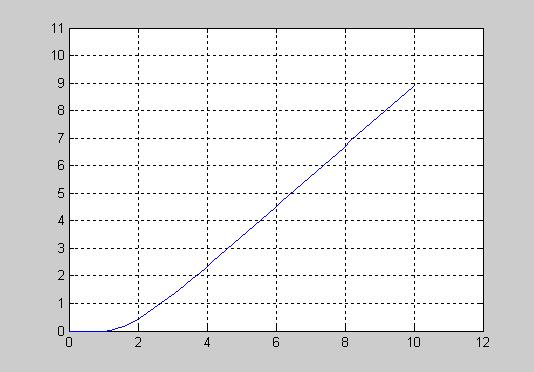
Построить переходной процесс в системе при Хвх =10:
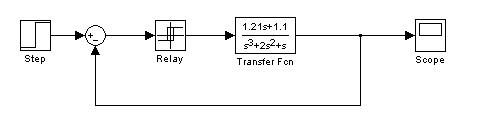
Переходной процесс:
Похожие работы
-
Разработка и расчет двухкаскадного усилителя с релейным выходом
На базе таких усилителей строят схемы нуль-индикаторов с мощностью срабатывания нескольких десятков микроватт, схемы измерительных органов защиты, подключаемые к маломощным датчикам, и исполнительные элементы с выходной мощностью до нескольких киловатт.
-
Математическая модель системы в переменных пространства состояний
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ В ПЕРЕМЕННЫХ ПРОСТРАНСТВА СОСТОЯНИЙ ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ Математическая модель системы в переменных пространства состояний имеет вид
-
Частотные критерии устойчивости
Исследования устойчивости разомкнутой и замкнутой систем. Понятие разомкнутой системы – системы, в которой отсутствует обратная связь между входом и выходом, то есть управляемая величина (выходная) не контролируется. Логарифмический частотный критерий.
-
Синтез САУ
Задание для курсовой работы по теории управления Исследовать систему, при обнаружении свойств, отрицательно влияющих на работоспособность системы, удалить их, или уменьшить их влияние. При необходимости обеспечить регулирование наилучшем регулятором.
-
Подходы к анализу нелинейной динамики жидкостей
Основная область моей научной деятельности - нелинейные явления в электрогидродинамике. Эти явления можно обнаружить, если наблюдать за поведением проводящей жидкости со свободной поверхностью во внешнем электрическом поле.
-
Анализ устойчивости системы автоматизированного управления двумя методами по критерию устойчивос
РЕФЕРАТ Контрольная работа: 12 страниц, 4 рисунков, 1 таблицу. Данная контрольная работа выполнена студентом факультета энергетического на тему: Анализ устойчивости САУ.
-
Интегралы. Функции переменных
Метод интегрирования по частям. Задача на нахождение частных производных 1-го порядка. Исследование на экстремум заданную функцию. Нахождение частных производных. Неоднородное линейное дифференциальное уравнение 2-го порядка. Условия признака Лейбница.
-
Нелинейные САУ
В проекте рассматривается о применении метода частотных круговых диаграмм к исследованию устойчивости систем, с логическими алгоритмами управления.
-
Опыт применения критерия Сильвестра в некоторых задачах устойчивости консервативных систем
Краткая биография английского математика Дж. Сильвестра. Устойчивость равновесия консервативной системы с конечным числом степеней свободы. Функции Ляпунова и критерий Сильвестра. Пример определения условия устойчивости равновесного положения системы.
-
Окружение и локализация корня нелинейной функции действительной переменной
Окружение и локализация корня нелинейной функции действительной переменной Важной проблемой поиска корня нелинейной функции действительной переменной является выяснение интервала, на котором корень содержится. Ниже приведен алгоритм поиска такого интервала и ограничения на его применение.