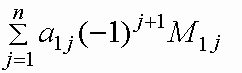Название: Математика матрица
Вид работы: реферат
Рубрика: Математика
Размер файла: 22.73 Kb
Скачать файл: referat.me-218220.docx
Краткое описание работы: Матрицы Матрица - прямоугольная (в частном случае квадратная) таблица с числами. Матрица m × n - это таблица из m строк и n столбцов. Если m = n, матрицу называют квадратной матрицей порядка n.
Математика матрица
Матрицы
Матрица - прямоугольная (в частном случае квадратная) таблица с числами.
Матрица m × n - это таблица из m строк и n столбцов. Если m = n, матрицу называют квадратной матрицей порядка n.
Пример матрицы 4×3 :
| a 1,1 |
a 1,2 |
a 1,3 |
| a 2,1 |
a 2,2 |
a 2,3 |
| a 3,1 |
a 3,2 |
a 3,3 |
| a 4,1 |
a 4,2 |
a 4,3 |
Определитель матрицы
Определитель матрицы A (обозначается как det A) это число, которое ставится в соответствие матрице A по определенному правилу.
Определитель существует (определен) только для квадратной матрицы.
Определителем квадратной матрицы A порядка n называется число:
| det(A)= |
|
= |
|
где M1,j - определитель квадратной матрицы порядка n -1, полученной из матрицы A вычеркиванием первой строки и j -го столбца, называемый минором элемента a1,j .
Выражение
| det A = |
|
называется формулой вычисления определителя разложением по первой строке.
Число (-1) j+1
M1,j
называется алгебраическим дополнением
элемента a1,j
.
Если вас пугает это формула, то она значит следующее:
- Определитель вычисляется как сумма n слагаемых, где n - порядок матрицы.
- Знак, с которым каждое слагаемое входит в сумму, определяется как (-1)1+k .
- Каждое слагаемое представляет собой произведение двух чисел: элемента первой строки матрицы на минор - определитель матрицы, получаемой из исходной путем вычеркивания 1 строки и j столбца.
Обратите внимание, что порядок минора на 1 меньше, чем у исходной матрицы!!!
Умножение матриц
Произведением матриц A размером m × n и матрицы B размера n × k называется матрица размера m × k, элементы которой определяются формулой
| ci,j = |
n |
a i,q · b q,j |
| ∑ |
||
| q=1 |
i=1, ... , m
j=1, ..., k
Произведение матриц записывается как C=A·B.
Произведение матриц определено, если число столбцов матрицы A равняется числу строк матрицы B!!!!
Для более легкого запоминания формулы умножения матриц существует простое правило: строка на столбец. Берем элементы из строки матрицы А и они умножаются на соответствующие элементы столбца матрицы B. Потом все произведения складываются и мы получаем значение элемента матрицы C.
Координаты элемента в результирующей матрице определяется как номер строки матрицы A и номер столбца матрицы B.
Транспонирование матриц
Транспонирование матрицы - это такая операция над матрицей, когда первая строка становится первым столбцом, вторая строка становится вторым столбцом и так далее...
В результате получается транспонированная матрица, обозначаемая как AT .
Обратная матрица
Матрица A-1 - называется обратной к матрице A, если выполняется условие A ·A-1 = A-1 ·A=E.
Для квадратной матрицы A обратная матрица существует тогда, когда det A ≠ 0.
Обратную матрицу находим следующим образом:

где Ai,j - алгебраические дополнения элементов матрицы A.
Похожие работы
-
Теорема Лапласа
Теоре?ма Лапла?са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году.
-
Матрицы и определители
Дисциплина: Высшая математика Тема: Матрицы и определители Понятие матрицы При изучении вопросов, связанных с действием над векторами, а также при изучении систем линейных уравнений приходится иметь дело с таблицами из чисел, которые называются матрицами.
-
Матрицы
Общие определения, связанные с понятием матрицы. Действия над матрицами. Определители 2-го и 3-го порядков, порядка n, порядок их вычисления и характерные свойства. Обратные матрицы и их ранг. Понятие и этапы элементарного преобразования матрицы.
-
Основы высшей математики
Понятие "матрица" в математике. Операция умножения (деления) матрицы любого размера на произвольное число. Операция и свойства умножения двух матриц. Транспонированная матрица – матрица, полученная из исходной матрицы с заменой строк на столбцы.
-
Решение матриц
Правила произведения матрицы и вектора, нахождения обратной матрицы и ее определителя. Элементарные преобразования матрицы: умножение на число, прибавление, перестановка и удаление строк, транспонирование. Решение системы уравнений методом Гаусса.
-
Матрица
Матрицей размерности m x n называется прямоугольная таблица m x n чисел a ij , i=1,..., m, j=1,..., n: расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).
-
Матрицы действия с ними
Контрольная работа на тему: «Матрицы, действия с ними» Историческая справка Понятие Матрица (в математике) было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами.
-
Матрицы графов
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра информатики РЕФЕРАТ На тему: «Матрицы графов» МИНСК, 2008 В теоретико-множественной и геометрической форм определения (задания) графов, часто используется матричная форма их представления. Существуют различные виды матриц графов, однако все они, как правило, полностью передают основные свойства графов.
-
Алгебра матриц
Основные понятия. Линейные операции над матрицами. Умножение матриц. Свойства умножения матриц. Вырожденные и невырожденные матрицы.
-
Матрицы и определители
Матрицы. Операции над матрицами. Определители. Теорема (разложение определителя по строке или столбцу).. Ранг матрицы. Обратная матрица.