Название: Решение матриц
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 119.48 Kb
Скачать файл: referat.me-217636.docx
Краткое описание работы: Правила произведения матрицы и вектора, нахождения обратной матрицы и ее определителя. Элементарные преобразования матрицы: умножение на число, прибавление, перестановка и удаление строк, транспонирование. Решение системы уравнений методом Гаусса.
Решение матриц
Умножение
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы .
Это условие не выполняется, произведение АВ не существует.
Произведение матрицы и вектора А b :
![]()
Скалярное произведение векторов ( b ,с):
![]()
Найти определитель матрицы А:
В частности, формула вычисления определителя матрицы ![]() такова:
такова:
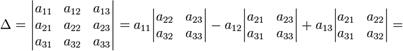
= a 11 a 22 a 33 − a 11 a 23 a 32 − a 12 a 21 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31
=2*(-4)*5 – 2*4*2 – (-2)*5*5 + (-2)*4*(-1) +(-1)*5*2 – (-1)*(-4)*(-1) = -40 – 16 +50 + 8 – 10 + 4 = -4
Найти обратную матрицу А-1 :
Решение .
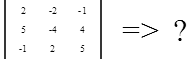
Определитель введенной Вами матрицы равен:
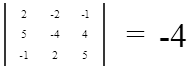
Определитель не равен нулю, следовательно обратная матрица существует.
Допишем к исходной матрице единичную матрицу справа.
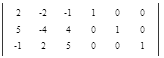
Начнем приведение левой квадратной матрицы к единичному виду. При помощи элементарных преобразований уберем все коэффициенты ниже главной диагонали.
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
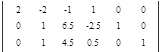
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
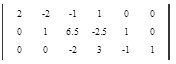
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
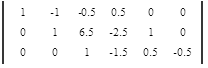
Приведем все коэффициенты выше главной диагонали к 0, при помощи элементарных преобразований.
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
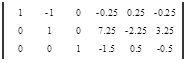
Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
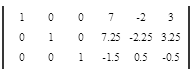
Ответ .
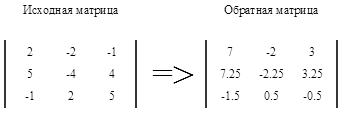
Как уже ранее упоминалось, мы при помощи элементарных преобразований переместили единичную матрицу из правой части в левую, при этом не нарушив ни одного правила работы с матрица.
Квадратная матрица, которую Вы видите справа и есть обратная матрица к введенной Вами .
Решение системы уравнений Ах= b :
Условие
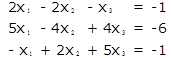
Решение
Найдем определитель главной матрицы, составленной из коэффициентов при X1 - n :
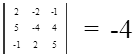
Определитель главной матрицы системы уравнений не равен нулю, следовательно данная система уравнений имеет единственное решение. Найдем его. Достоим главный определитель системы уравнений еще одним столбцом, в который вставим значения за знаком равенства.
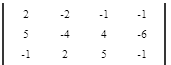
Теперь последовательно, при помощи элементарных преобразований преобразуем левую часть матрицы (3 × 3) до треугольного вида (обнулим все коэффициенты находящиеся не на главной диагонали, а коэффициенты на главной диагонали преобразуем до единиц).
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
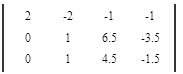
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
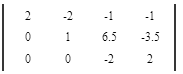
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
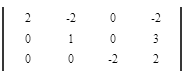
Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
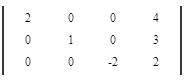
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
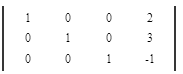
Ответ .
Числа получившиеся правее единичной матрицы и будут решением Вашей системы уравнений.
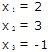
Элементарные преобразования матрицы
Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки матрицы на число, отличное от нуля; 2) прибавление к одной строке матрицы другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование матрицы ;
Те же операции, применяемые для столбцов матрицы , также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу матрицы прибавить линейную комбинацию остальных строк (столбцов).
Начинаем решать вот такую систему уравнений методом Гаусса

Определитель основной матрицы равен -4
Хотим сделать элемент [1,1] равным 1. Разделили всю строку 1 на элемент [1,1]=2.
![]()
Сделали в 1 строке элемент 1 единичным.
Обнулим 1 столбец: Из 2 строки вычли 1 строку , умноженную на элемент [1,2]=5.
![]()
Из 3 строки вычли 1 строку , умноженную на элемент [1,3]=-1.
![]()
Преобразование 1 столбца сделали.
Хотим сделать элемент [2,2] равным 1. Разделили всю строку 2 на элемент [2,2]=1.
![]()
Сделали в 2 строке элемент 2 единичным.
Обнулим 2 столбец: Из 1 строки вычли 2 строку , умноженную на элемент [2,1]=-1.
![]()
Из 3 строки вычли 2 строку , умноженную на элемент [2,3]=1.

Преобразование 2 столбца сделали.
Хотим сделать элемент [3,3] равным 1. Разделили всю строку 3 на элемент [3,3]=-2.

Сделали в 3 строке элемент 3 единичным.
Из 1 строки вычли 3 строку , умноженную на элемент [3,1]=6.

Из 2 строки вычли 3 строку , умноженную на элемент [3,2]=6.5.

Преобразование 3 столбца сделали.
Ну вот вроде и все. Решение содержится в правом столбце: ![]() Быстренько сделаем проверку: Исходная матрица:
Быстренько сделаем проверку: Исходная матрица:
![]()
Подставим в исходную матрицу полученные решения: в квадратных скобках элементы матрицы, в круглых решения системы уравнений
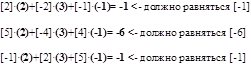
Похожие работы
-
Системы линейных уравнений и неравенств
Основные понятия теории систем уравнений. Метод Гаусса — метод последовательного исключения переменных. Формулы Крамера. Решение систем линейных уравнений методом обратной матрицы. Теорема Кронекер–Капелли. Совместность систем однородных уравнений.
-
Математика матрица
Матрицы Матрица - прямоугольная (в частном случае квадратная) таблица с числами. Матрица m × n - это таблица из m строк и n столбцов. Если m = n, матрицу называют квадратной матрицей порядка n.
-
Матрицы
Общие определения, связанные с понятием матрицы. Действия над матрицами. Определители 2-го и 3-го порядков, порядка n, порядок их вычисления и характерные свойства. Обратные матрицы и их ранг. Понятие и этапы элементарного преобразования матрицы.
-
Основы высшей математики
Понятие "матрица" в математике. Операция умножения (деления) матрицы любого размера на произвольное число. Операция и свойства умножения двух матриц. Транспонированная матрица – матрица, полученная из исходной матрицы с заменой строк на столбцы.
-
Алгебра матриц. Системы линейных уравнений
Выполнение действий над матрицами. Определение обратной матрицы. Решение матричных уравнений и системы уравнений матричным способом, используя алгебраические дополнения. Исследование и решение системы линейных уравнений методом Крамера и Гаусса.
-
Теория Матриц и Определителей
Средняя школа № 45. Город Москва. Ученик 10 класса “Б” Горохов Евгений Курсовая работа (черновик). Введение в теорию матриц и определителей
-
Матрицы действия с ними
Контрольная работа на тему: «Матрицы, действия с ними» Историческая справка Понятие Матрица (в математике) было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами.
-
Определители матрицы и системы линейных алгебраических уравнений
Основные действия над матрицами, операция их умножения. Элементарные преобразования матрицы, матричный метод решения систем линейных уравнений. Элементарные преобразования систем, методы решения произвольных систем линейных уравнений, свойства матриц.
-
Системы линейных уравнений
Критерий совместности. Метод Гаусса. Формулы Крамера. Матричный метод.
-
Матрицы и определители
Матрицы. Операции над матрицами. Определители. Теорема (разложение определителя по строке или столбцу).. Ранг матрицы. Обратная матрица.