Referat.me
/ / Экстремумы функций 3

Название: Экстремумы функций 3

Вид работы: реферат

Рубрика: Математика

Размер файла: 21.33 Kb

Скачать файл: referat.me-218256.docx

Краткое описание работы: Экстремумы функции На рисунке 123 изображён график функции y= . Рассмотри окрестности точки , т.е. некоторый интервал содержащий эту точку. Как видно из рисунка, существует такая окрестность точки

Экстремумы функций 3

Экстремумы функции

На рисунке 123 изображён график функции y=-3. Рассмотри окрестности точки x =0 , т.е. некоторый интервал содержащий эту точку. Как видно из рисунка, существует такая окрестность точки x =0 , что наибольшее значение функ­ция -3 в этой окрестности принимает в точ­ке x = 0. Например, на интервале (—1; 1) наи­большее значение, равное 0, функция принимает в точке x =0. Точку x = 0 называют точкой мак­симума этой функции.

Аналогично точку x = 2 называют точкой мини­мума функции x —Зх2 , так как значение функ­ции в этой точке меньше ее значения в любой точке некоторой окрестности точки x =2, напри­мер окрестности (1,5; 2,5).

Точка называется точкой максимума функции (x ), если существует такая окрестность точки , что для всех x х0 из этой окрестности выпол­няется неравенство

f(x)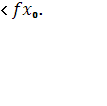

Например, точка хо = 0 является точкой макси­мума функции f ( x ) =1—х2 , так как f (0)=1 и при всех значениях x верно неравенство f ( x ) <1 (рис. 124).

Точка х0 называется точкой минимума функции f(x), если существует такая окрестность точки х0 , что для всех x х0 из этой окрестности выполня­ется неравенство

f(x)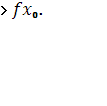

Например, точка х0 =2 является точкой миниму­ма функции f(x) =3+(x— 2)2 , так как /(2) = 3 и /(х)>3 при всех значениях хф2 (рис. 125).

Точки минимума и точки максимума называются точка­ ми экстремума.

Рассмотрим функцию /(х), которая определена в некоторой окрестности точки х0 и имеет произ­водную в этой точке.

Теорема. Если х0 — точка экстремума диффе­ренцируемой функции /(х), то /'(х0 ) = 0.

Это утверждение называют теоремой Ферма1 . Теорема Ферма имеет наглядный геометрический смысл: касательная к графику функции г/ = /(х) в точке (х0 ; / (х0 ), где х0 — точка экстремума функ­ции г/ = /(х), параллельна оси абсцисс, и поэто­му ее угловой коэффициент /'(х0 ) равен нулю (рис. 126). Например, функция / (х) = 1 — х2 (рис. 124) имеет

Похожие работы

  • по Математике 2

    Содержание 1.Введение в анализ и дифференциальное исчисление функции одного переменного. 2 2. Дифференциальное исчисление функций и его приложение 5

  • Контрольная работа по Математике 3

    МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНСТИТУТДИСТАНЦИОННОГО ОБРАЗОВАНИЯ Кафедра «Бухгалтерский учет, анализ и аудит»

  • Дифференциальное исчисление функций

    Содержание 1. Введение в анализ и дифференциальное исчисление функции одного переменного 2. Дифференциальное исчисление функций и его приложение 3. Интегральное исчисление функции одного переменного

  • Экстремумы функций многих переменных

    Понятие экстремума. Необходимые и достаточные условия экстремума.

  • Экстремумы функций 2

    Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке. Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В точке x3 функция, очевидно, также имеет максимум. Если рассмотреть точку x2, то в ней значение функции меньше всех соседних значений.

  • Модели и методы принятия решений

    Нахождение экстремумов функций методом множителей Лагранжа. Выражение расширенной целевой функции. Схема алгоритма численного решения задачи методом штрафных функций в сочетании с методом безусловной минимизации. Построение линий ограничений.

  • Дифференцирование. Интегрирование

    Методика и основные этапы нахождения производной функции. Исследование методами дифференциального исчисления и построение графика функции. Порядок определения экстремумов функции. Вычисление неопределенных и определенных интегралов заменой переменной.

  • Исследование функций

    Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа и их доказательство. Локальные экстремумы функции, исследование ее на выпуклость и вогнутость, понятие точки перегиба. Асимптоты и общая схема построения графика функции.

  • Основные элементарные функции, их свойства и графики

    Национальный научно-исследовательский университет -ИрГТУ- Кафедра прикладной геологии Реферат по высшей математике На тему: «Основные элементарные функции,

  • Экстремумы функции

    Построение графика непрерывной функции. Определение множителя Лагранжа. Критические точки - значения аргумента из области определения функции, при которых производная функции обращается в нуль. Наибольшее и наименьшее значения функции на отрезке.