Название: Дифференцирование. Интегрирование

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 83.04 Kb

Скачать файл: referat.me-215770.docx

Краткое описание работы: Методика и основные этапы нахождения производной функции. Исследование методами дифференциального исчисления и построение графика функции. Порядок определения экстремумов функции. Вычисление неопределенных и определенных интегралов заменой переменной.

Дифференцирование. Интегрирование

Задание 1. Найти производные функций

a)

Пусть , , тогда

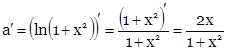
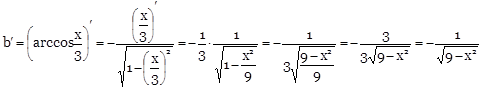
b)

Если функция имеет вид , то её производная находится по формуле .

Перейдем от десятичного логарифма к натуральному:

По свойству логарифма

Таким образом,

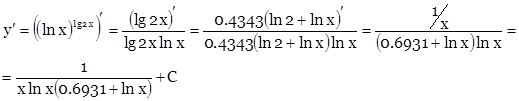
c)

Продифференцируем уравнение, считая y функцией от х:

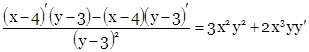
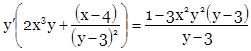
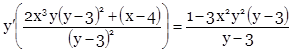
Задание 2. Исследовать методами дифференциального исчисления и построить график функции

Областью определения функции являются все действительные числа,

кроме х=0. В точке х=0 функция разрывна .

Функция нечетная , т. к.

Функция не пересекается с осями координат (уравнение y =0 не имеет решений).

Найдем производную функции:

.

Найдем стационарные точки, приравняв производную к нулю.

Функция возрастает в промежутке (-∞; – 1) U (1; ∞)

и убывает в промежутке (-1; 0) U (0; 1).

Функция имеет экстремумы : максимум – в точке х=-1, минимум – в точке х=1.

Исследуем функцию на выпуклость / вогнутость .

Для этого найдем производную второго порядка и, приравняв её к нулю, вычислим критические точки второго рода.

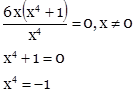
В точке х=0 вторая производная не существует, т. к. это точка разрыва функции. В интервале (-∞; 0) <0, следовательно, график функции в этом интервале выпуклый. В интервале (0;∞) >0, следовательно, график функции в этом интервале вогнутый.

Асимптоты графика функции :

1) вертикальная асимптота – прямая х=0

Т.к. и

2) горизонтальных асимптот нет,

т. к. и

3) наклонных асимптот нет,

т. к.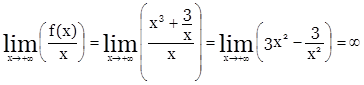

и

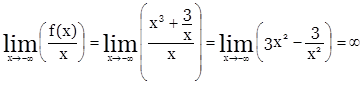
Задание 3 . Найти экстремумы функции Z = ln (3 – x ² + 2 x – y ² )

Найдем частные производные первого порядка.

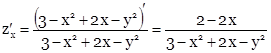
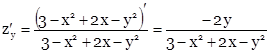
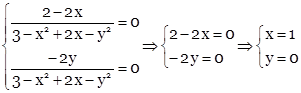
М (1; 0) – стационарная точка.

Найдем вторые производные и их значения в точке М.

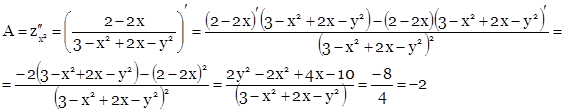
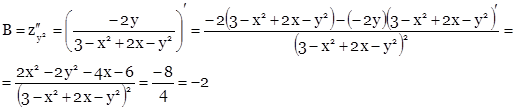
>0 Следовательно, функция Z = ln (3 – x ² + 2 x – y ² ) имеет экстремум в точке М (1; 0) – максимум, т. к. A < 0.

Задание 4 . Вычислить неопределенные интегралы, результат проверить дифференцированием

a)

Решаем методом замены переменной. Положим ,

тогда ,

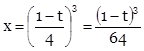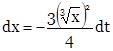
Таким образом, получаем

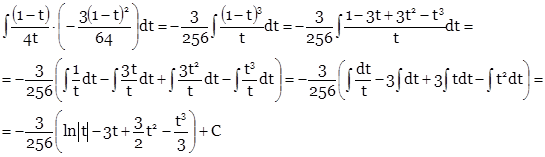
Вернемся к переменной х.

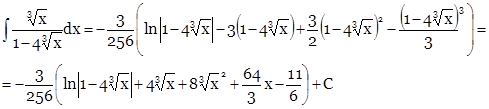
Проверим дифференцированием:

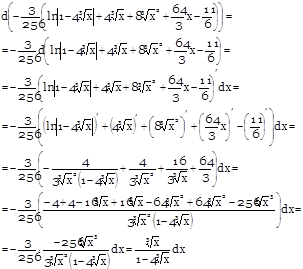
b)

Воспользуемся таблицей неопределенных интегралов [Выгодский, М.Я. Справочник по высшей математике. – М.: Наука, 1972. – 872 с.:ил. – С. 850]

С

Проверим дифференцированием:

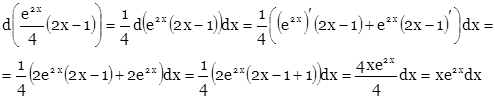
c)

Неправильную рациональную дробь приводим к правильной делением числителя на знаменатель, получаем

Согласно свойству интервала алгебраической суммы, имеем

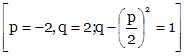
Подстановка приводит интеграл к виду

Возвращаясь к аргументу х, получаем

Таким образом, ,

где С=С₁ +С₂

Проверим дифференцированием:

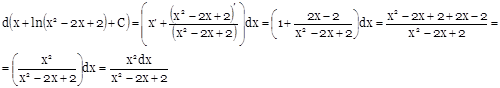
Задание 5 . Вычислить определенный интеграл

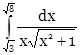
Сначала вычислим неопределенный интеграл методом замены переменной. Полагая , находим

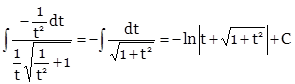
Вернемся к переменной х.

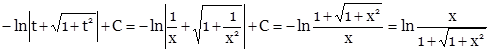
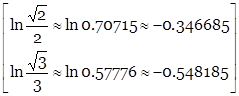Таким образом ,

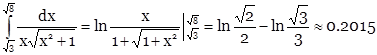
Библиографический список

1. Баврин, И.И. Высшая математика: учебник/ И.И. Баврин. – М.: Академия, 2003. – 616 с.:ил.

2. Выгодский, М.Я. Справочник по высшей математике/М.Я. Выгодский. – М.: Наука, 1972. – 872 с.:ил.

3. Выгодский, М.Я. Справочник по элементарной математике/М.Я. Выгодский. – СПб.: Изд. «Санкт-Петербург оркестр», 1994. – 416 с.:ил.