Название: Инструменты Фибоначчи для анализа валютного рынка

Вид работы: статья

Рубрика: Математика

Размер файла: 196.41 Kb

Скачать файл: referat.me-218526.docx

Краткое описание работы: Леона?рдо Фибоначчи или Леонардо Пизанский (Leonardo Pisano, Fibonacci; в переводе с итальянского «сын Боначчи») – выдающийся математик средневековья. Жил в городе Пиза, в Италии. Он стал современником строительства знаменитой Пизанской башни.

Инструменты Фибоначчи для анализа валютного рынка

Кормилицына Ирина

Гениальный математик

Годы жизни Фибоначчи точно неизвестны: 1170/1180-1240/1250.

Леона́рдо Фибоначчи или Леонардо Пизанский (Leonardo Pisano, Fibonacci; в переводе с итальянского «сын Боначчи») – выдающийся математик средневековья. Жил в городе Пиза, в Италии. Он стал современником строительства знаменитой Пизанской башни.

Фибоначчи жил в эпоху правления императора Фридриха II. Фридрих II не любил кровавых состязаний, а вместо этого проводил соревнования по математике. Именно на таких научных «турнирах» и был замечен талант Леонардо Фибоначчи. Благодаря своему отцу, Леонардо получил хорошее образование.

Заручившись поддержкой самого императора Фибоначчи выпустил ряд научных трактатов:

- «Книга абака» (Liber abaci) (1202 г.)

- «Практики геометрии» (Practica geometriae) (1220 г.)

- «Книга квадратов» (Liber quadratorum) (1225 г.)

По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику чуть ли не до времён Декарта (XVII в.).

Наиболее значимым из трудов Фибоначчи считается «Книга абака», где он описал последовательность Фибоначчи. Эта книга представляет собой объёмный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с арабскими цифрами. В своих трудах Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна ещё в древнейшие времена под названием «золотое сечение».

Волшебные числа

Числа Фибоначчи – это элементы числовой последовательности 1, 1, 2, 3, 5, 8, ... (ряда Фибоначчи), в которых каждый последующий член равен сумме двух предыдущих. Числа Фибоначчи обладают и рядом других закономерностей.

Так, например, отношение текущего числа ряда Фибоначчи к предыдущему числу стремится к значению 1.618034. Отношение текущего числа ряда Фибоначчи к последующему числу стремится к значению 0.618034. Отношение текущего числа ряда Фибоначчи к последующему через одно от текущего числа стремится к значению 0.381966.

Уровни Фибоначчи

Уровни Фибоначчи (Fibonacci Retracement) используются для измерения длины коррекции. Как правило, сильные восходящие или нисходящие движения периодически сопровождаются так называемыми коррекциями, т.е. движением в обратном основному движению направлении. После сильного роста или падения цены часто возвращаются назад, корректируя значительную долю своего первоначального движения. В ходе этого коррекционного движения цены часто встречают поддержку/сопротивление на уровнях линий Фибоначчи или вблизи них.

Уровни Фибоначчи стоит растягивать в тот момент, когда Вы начинаете предполагать, что основная действующая тенденция замедляется, т.е. входит в фазу коррекции. На восходящем тренде уровни необходимо растягивать снизу вверх, на нисходящем – наоборот, сверху вниз.

Рассмотрим пример. В паре евро/доллар действует долгосрочная восходящая тенденция. На рисунке 1 основной восходящий тренд обозначен сиреневыми линиями. Мы наблюдали сильное восходящее движение от $1.2480 до $1.3360, после чего это движение затормозилось, и пара вступила в фазу коррекции. Растянув Fibo от $1.2480 до $1.3360, мы увидели, что длина коррекции составила 50.0. Это считается довольно глубокой коррекцией. Фаза коррекции сменилась сильным восходящим движением ($1.2860-$1.3680). Далее снова последовала нисходящая коррекция. Стоит отметить, что после того, как Вы убедились, что пара вышла из стадии коррекции, уровни Фибоначчи целесообразно удалить. Не стоит загромождать график «старыми» Фибоначчи.

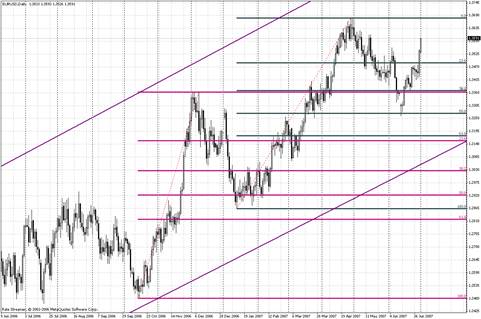
Рисунок 1. Уровни коррекции Фибоначчи.

Нередко уровни Фибоначчи совпадают с силовыми уровнями.

Веер Фибоначчи

При построении веера Фибоначчи (Fibonacci Fan) две экстремальные точки соединяются прямой. На восходящем тренде веер растягивается от впадины до противостоящего пика, на нисходящем – наоборот. Затем через вторую экстремальную точку автоматически проводится «невидимая» вертикальная линия (на рисунке 2 она обозначена красным цветом). Далее из первой экстремальной точки проводятся три линии тренда, пересекающие невидимую вертикальную линию на уровнях Фибоначчи 38, 2%, 50% и 61, 8%. Считается, что эти линии представляют собой уровни сопротивления и поддержки.

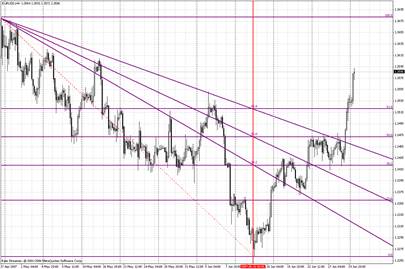
Рисунок 2. Веер Фибоначчи.

Дуги Фибоначчи

При построении дуг Фибоначчи (Fibonacci Arcs) две экстремальные точки соединяются прямой. На восходящем тренде эта прямая растягивается от минимума к максимуму, на нисходящем - наоборот. Далее наносятся три дуги с центром во второй экстремальной точке, пересекающие линию тренда на уровнях Фибоначчи 38, 2%, 50% и 61, 8%.

Дуги Фибоначчи используются в качестве уровней поддержки и сопротивления. Возможно использовать комбинацию из дуг и вееров Фибоначчи. В этом случае на ценовой график наносятся одновременно и дуги, и веера Фибоначчи, а уровни поддержки/сопротивления определяются точками пересечения этих линий.

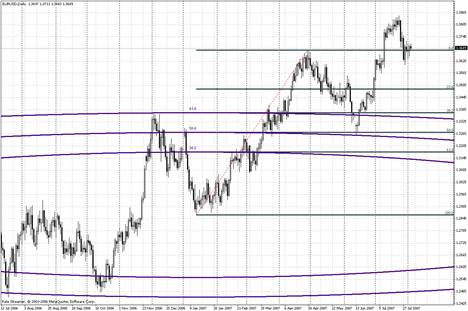
Рисунок 3. Дуги Фибоначчи.

При использовании дуг Фибоначчи необходимо помнить, что точки пересечения дуг с ценовым графиком могут изменяться в зависимости от временного периода графика (час, день, неделя и т.д.). Это объясняется тем, что дуга - это часть окружности, и ее форма всегда неизменна.

Довольно хороший результат дает комбинация различных инструментов Фибоначчи.